#RANK_3 1191:棋盘分割

Posted 2020-11-07 qianwagui

总时间限制: 

1000ms

 

内存限制: 

65536kB

描述

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

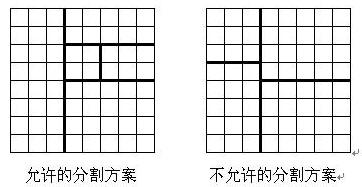
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差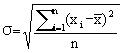，其中平均值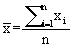，xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n，求出O‘的最小值。

输入

第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出

仅一个数，为O‘（四舍五入精确到小数点后三位）。

样例输入

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

样例输出

1.633

来源

Noi 99

#include <iostream>
#include <cstring>
#include <cmath>
#include <stdio.h>
#include <iomanip>
#define INF 1000000000 
using namespace std;
int grid[9][9];
int f[18][9][9][9][9];
int sum[0x10][0x10];
int getsum (int x1, int x2, int y1, int y2);
int seperate(int n, int x1, int x2, int y1, int y2){
    if (f[n][x1][x2][y1][y2] != -1 ) return f[n][x1][x2][y1][y2];
    if ( x1 == x2 && y1 == y2 ) {
        if ( n== 0 ) f[n][x1][x2][y1][y2] = grid[x1][y2] * grid[x1][y2];
        else f[n][x1][x2][y1][y2] = INF;
        return f[n][x1][x2][y1][y2];
    }
    if (n==0) {
        f[n][x1][x2][y1][y2] = getsum ( x1, x2, y1, y2);
        return f[n][x1][x2][y1][y2];
    }
    int tmp = INF;
    for (int i = x1; i< x2; i++){
        tmp = min(tmp, seperate( n-1, x1, i, y1, y2) + seperate( 0, i+1, x2, y1, y2));
        tmp = min(tmp, seperate( n-1, i+1, x2, y1, y2) + seperate( 0, x1, i, y1, y2));
    }
    for (int i = y1; i < y2; i++){
        tmp = min(tmp, seperate( n-1, x1, x2, y1, i) + seperate( 0, x1, x2, i+1, y2));
        tmp = min(tmp, seperate( n-1, x1, x2, i+1, y2) + seperate( 0, x1, x2, y1, i));
    }
    f[n][x1][x2][y1][y2] = tmp;
    return f[n][x1][x2][y1][y2];
}
int getsum (int x1, int x2, int y1, int y2){
    int tmp = sum[x2][y2];
    if (x1>=2) tmp -= sum[x1 - 1][y2];
    if (y1 >=2) tmp -= sum[x2][y1 - 1];
    if (x1 >=2 && y1 >= 2) tmp += sum[x1 - 1][y1 - 1];
    return tmp * tmp;
}

int main(){
    memset (sum, -1, sizeof(sum));
    memset (f, -1, sizeof(f));
    int n;
    cin >> n;
    for (int i = 1; i <= 8; i++){
        for ( int j = 1; j <= 8; j++){
            cin >> grid[i][j];
        }
    }
    sum[1][1] = grid[1][1];
    for (int i = 2 ; i < 9; i++) {
        sum[i][1] = sum[i - 1][1] + grid[i][1];
        sum[1][i] = sum[1][i - 1] + grid[1][i];
    }
    for (int i = 2; i < 9; i++) {
        for (int j = 2; j < 9; j++) {
        sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + grid[i][j];
        }
    }  
    cout <<setiosflags(ios::fixed) <<setprecision(3)<< sqrt((seperate( n - 1, 1, 8, 1, 8) - (sum[8][8] * sum[8][8] * 1.0 / n))/n) ;
} 

View Code

课上的例题，没想到自己写的时候却用了这么长时间……而且基本还是看着写的

最后输出的时候的数学表达式没弄明白；以及getsum函数中，由于和例程下标不一样，导致直接抄来的getsum求和时越界了……

把if(x1) 改成 if（x1 >= 2） 就好了。

 

关于这道题，思路还是比较清楚的，直接模拟分割变得到了递归函数。这一点很明白。

关键在于递归时又用了记忆化搜索的方法，直接开一个一个五维数组来存储结果，在使用记忆化搜索搜索时，典型的模板是

if (f[i][j][k] != -1) return f[i][j][k];
……
<class T> T result;
f[i][j][k] = result;
return f[i][j][k];

另外此题的数学处理也是很有趣的……又暴露了自己数学功底不扎实，或者说是压根不愿意进一步去想如何使问题更加简单。这是不对的。