POJ 1191 棋盘分割 DFS记忆化搜索经典

Posted 2020-12-30 ymzjj

题目传送门：http://poj.org/problem?id=1191

棋盘分割

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 16150		Accepted: 5768

Description

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行) 

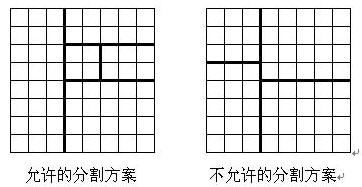
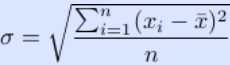
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。 
均方差 

其中平均值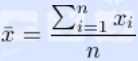 
x_i为第i块矩形棋盘的总分。 
请编程对给出的棋盘及n，求出O‘的最小值。 

Input

第1行为一个整数n(1 < n < 15)。 
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。 

Output

仅一个数，为O‘（四舍五入精确到小数点后三位）。

Sample Input

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

Sample Output

1.633

Source

Noi 99

 

题意概括：

中文题，不容小觑。

解题思路：

一、DFS搜索，每次分割棋盘可以选择两个方向 横切（改变Y的范围） 或者 竖切（改变X的范围）；选择切割方向之后需要选择舍弃两部分之中的其中一部分，继续DFS另一部分。

二、但单纯的搜索太慢，我们可以发现其实是因为有很多子问题重叠，所以不妨用一个四维数组记录每次小矩形的运算结果，数组下标为小矩阵左上角和右下角的坐标。

三、公式化简：

 

AC code：

 1 ///POJ 1191 棋盘分割 （记忆化搜索经典）
 2 #include <cstdio>
 3 #include <iostream>
 4 #include <algorithm>
 5 #include <cstring>
 6 #include <cmath>
 7 #define INF 0x3f3f3f3f
 8 #define ll long long int
 9 #define mod 1000000007
10 using namespace std;
11 
12 const int MAXN = 15;
13 const int MAXM = 10;
14 double d[MAXN][MAXM][MAXM][MAXM][MAXM];
15 double record[MAXM][MAXM][MAXM][MAXM];
16 double mmp[MAXM][MAXM];
17 double sum, ave;
18 int N;
19 
20 double get_sum(int x1, int y1, int x2, int y2)
21 {
22     if(record[x1][y1][x2][y2]>=0) return record[x1][y1][x2][y2];
23     double re = 0;
24     for(int i = x1; i <= x2; i++)
25     for(int j = y1; j <= y2; j++)
26             re+=mmp[i][j];
27     record[x1][y1][x2][y2] = re*re;
28     return record[x1][y1][x2][y2];
29 }
30 
31 double dfs(int x1, int y1, int x2, int y2, int cnt)
32 {
33     if(d[cnt][x1][y1][x2][y2]>=0) return d[cnt][x1][y1][x2][y2];
34     if(cnt == N)
35     {
36         return get_sum(x1, y1, x2, y2);
37     }
38     double min_sum = 99999999;
39     double tp = 0;
40     for(int i = x1; i < x2; i++)
41     {
42         tp = get_sum(x1, y1, i, y2) + dfs(i+1, y1, x2, y2, cnt+1);
43         if(min_sum > tp) min_sum = tp;
44         tp = get_sum(i+1, y1, x2, y2) + dfs(x1, y1, i, y2, cnt+1);
45         if(min_sum > tp) min_sum = tp;
46     }
47     for(int j = y1; j < y2; j++)
48     {
49         tp = get_sum(x1, y1, x2, j) + dfs(x1, j+1, x2, y2, cnt+1);
50         if(min_sum > tp) min_sum = tp;
51         tp = get_sum(x1, j+1, x2, y2) + dfs(x1, y1, x2, j, cnt+1);
52         if(min_sum > tp) min_sum = tp;
53     }
54     d[cnt][x1][y1][x2][y2] = min_sum;
55     return min_sum;
56 }
57 
58 int main()
59 {
60     scanf("%d", &N);
61     memset(d, -1, sizeof(d));
62     memset(record, -1, sizeof(record));
63     for(int i = 1; i <= 8; i++)
64     for(int j = 1; j <= 8; j++)
65     {
66         scanf("%lf", &mmp[i][j]);
67         sum+=mmp[i][j];
68     }
69     ave = sum/(N*1.0);
70     ave*=ave;
71     double res = dfs(1, 1, 8, 8, 1);
72     double ans = sqrt(res/N-ave);
73     printf("%.3f
", ans);
74     return 0;
75 }