有重边与无重边的无向图的割边求法

Posted 2020-11-05 MekakuCityActor

无向图无重边：也就每两个顶点之间最多有一条边相连【也就是根据顶点编号即可确定边】【如下】

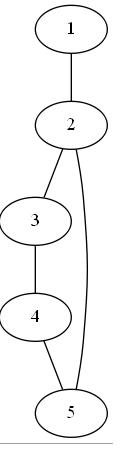
无向图有重边如：顶点1与顶点2有两条或更多的边直接相连【也就是不能根据顶点编号来确定边】【如下】

 

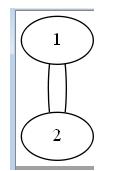
首先介绍无重边的无向图的割边求法：由于无重边的无向图中可以根据顶点来确定边，所以函数中的参数 u 和 fa  都是顶点。

 1 #include <stdio.h>
 2 #include <string.h>
 3 #include <vector>
 4 using namespace std;
 5 const int N = 1000 + 10;
 6 vector<int> g[N];
 7 int dfs_clock,pre[N];
 8 int cnt;
 9 int dfs(int u, int fa)
10 {
11     int lowu = pre[u] = ++dfs_clock;
12     int i,v,lowv;
13     for(i=0; i<g[u].size(); ++i)
14     {
15         v = g[u][i];
16         if(!pre[v])
17         {
18             lowv = dfs(v,u);
19             lowu = min(lowu,lowv);
20             if(lowv > pre[u])//相对于割点，只把等号给去掉了
21                 cnt++;
22         }
23         else if(v!=fa && pre[v]<lowu)//v!=fa 因为无重边，所以由v != fa来防止一条边的端点反复使用两次，从而避免使原本是桥的边判定为了不是桥，但也正因为它不更新父节点导致了其不能处理重边
24             lowu = pre[v];
25     }
26     return lowu;
27 }
28 int main()
29 {
30     int i,x,y;
31     int n,m;
32     scanf("%d%d",&n,&m);
33     for(i=0; i<m; ++i)
34     {
35         scanf("%d%d",&x,&y);
36         g[x].push_back(y);
37         g[y].push_back(x);
38     }
39     dfs(1,-1);
40 
41     printf("%d\\n",cnt);
42 }

下面是有重边的无向图的割边求法：由于有重边的无向图中不可以根据顶点来确定边，所以函数中的参数 u 是顶点，而 id 是边的编号。

 1 #include"string.h"  
 2 #include"stdio.h"  
 3 #include"iostream"  
 4 #define M 1111  
 5 #define inf 999999999  
 6 using namespace std;  
 7 struct st  
 8 {  
 9     int u,v,w,next;  
10 }edge[M*M*2];  
11 int head[M],dfn[M],low[M],bridge[M],n,t,index,num,mini,flag;  
12 void init()  
13 {  
14     t=0;  
15     memset(head,-1,sizeof(head));  
16 }  
17 void add(int u,int v,int w)  
18 {  
19     edge[t].u=u;  
20     edge[t].v=v;  
21     edge[t].w=w;  
22     edge[t].next=head[u];  
23     head[u]=t++;  
24 }  
25 void tarjan(int u,int id)  
26 {  
27     dfn[u]=low[u]=++index;  
28     int i;  
29     for(i=head[u];i!=-1;i=edge[i].next)  
30     {  
31         if(i==(1^id))continue; //和无重边的无向图通过v!=fa来避免同一条边重复遍历的处理方式不一样，这个是利用一条边的编号的异或关系来避免重复遍历的 
32         int v=edge[i].v;  
33         if(!dfn[v])  
34         {  
35             tarjan(v,i);  
36             low[u]=min(low[u],low[v]);  
37             if(low[v]>dfn[u])  
38             {  
39                 bridge[num++]=i;  
40                 if(mini>edge[i].w)  
41                     mini=edge[i].w;  
42             }  
43   
44         }  
45         else
46         low[u]=min(low[u],dfn[v]);  //由于上面已经对同一条边进行规避了，所以不需要使用多余的判断，直接就能更新了 
47     }  
48 }  
49 void solve()  
50 {  
51     index=num=flag=0;  
52     memset(dfn,0,sizeof(dfn));  
53     memset(low,0,sizeof(low));  
54     for(int i=1;i<=n;i++)  
55     {  
56         if(!dfn[i])  
57         {  
58             flag++;  
59             tarjan(i,-1);  
60         }  
61   
62     }  
63 }  
64 int main()  
65 {  
66     int m;  
67     while(scanf("%d%d",&n,&m),m||n)  
68     {  
69         init();  
70         while(m--)  
71         {  
72             int a,b,c;  
73             scanf("%d%d%d",&a,&b,&c);  
74             add(a,b,c);  
75             add(b,a,c);  
76         }  
77         mini=inf;  
78         solve();  
79         if(flag>1)  
80             printf("0\\n");  
81         else if(num==0)  
82             printf("-1\\n");  
83         else  
84         {  
85             if(mini==0)  
86                 printf("1\\n");  
87             else  
88                 printf("%d\\n",mini);  
89         }  
90     }  
91 }