汉诺塔(Tower of Hanoi)问题的求解——利用栈与递归

Posted 2020-07-10 Cainv89

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了汉诺塔(Tower of Hanoi)问题的求解——利用栈与递归相关的知识，希望对你有一定的参考价值。

汉诺塔(Tower of Hanoi)问题的求解——利用栈与递归

1. 汉诺塔问题的提法

汉诺塔问题是使用递归解决问题的经典范例。
传说婆罗门庙里有一个塔台，台上有3根标号为A、B、C的用钻石做成的柱子，在A柱上放着64个金盘，每一个都比下面的略小一点。把A柱上的金盘全部移到C柱上的那一天就是世界末日。
移动的条件是：一次只能移动一个金盘，移动过程中大金盘不能放在小金盘上面。庙里的僧人一直在移个不停，移动的最少总次数是 $2^{64}-1$ 次，如果每秒移动一次的话，需要500亿年。

2. 求解汉诺塔问题的算法原理

注：最少的移动总次数 = $2^{n}-1$ (n为盘子的个数)
如果n=1，则将这一个盘子直接从A柱移到C柱上，最少移动 $2^{1}-1$ = 1次。
如果n>1，则执行以下3步，最少移动 $2^{n}-1$ 次：
(1)用C柱做过滤，将A柱上的(n-1)个盘子移到B柱上。
(2)将A柱上最后一个盘子直接移到C柱上。
(3)用A柱做过滤，将B柱上的(n-1)个盘子移到C柱上。
汉诺塔问题(n=3)的求解过程示例图：

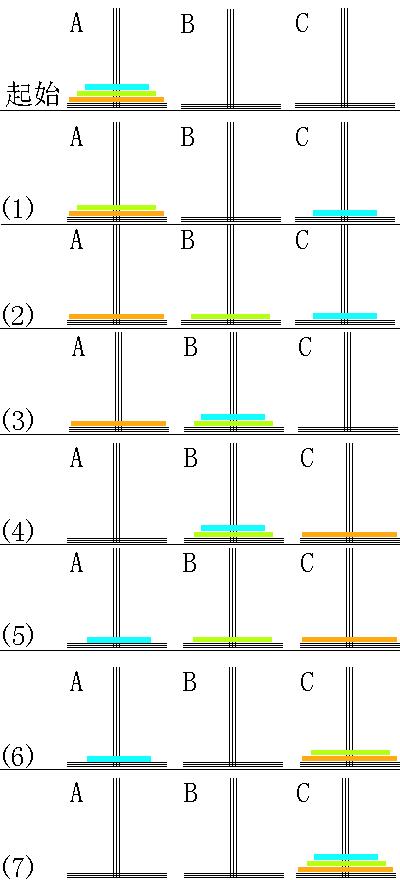
3. 利用递归求解汉诺塔问题

3.1 汉诺塔问题的递归求解算法实现

文件：Hanoi.h


#pragma once



#include <iostream>


#include <string>


using namespace std;

static int total_count = 0;
void Hanoi(int n, string A, string B, string C)
{
    if (n == 1)
    {
        total_count++;
        cout << total_count<< ": Move top disk from peg" << A << " to peg" << C << endl;
    }
    else
    {
        Hanoi(n - 1, A, C, B);
        total_count++;
        cout << total_count<< ": Move top disk from peg" << A << " to peg" << C << endl;
        Hanoi(n - 1, B, A, C);
    }
}

3.2 主函数(main函数)的实现

文件：main.cpp


#include "Hanoi.h"


int main()
{
    Hanoi(3, "A", "B", "C");
    system("pause");
    return 0;
}

4. 利用栈与递归求解汉诺塔问题

4.1 链表结点结构的定义

文件：LinkNode.h


#ifndef LINK_NODE_H_


#define LINK_NODE_H_



#include <iostream>


#include <string>


#include <strstream>


using namespace std;

template <class T>
struct LinkNode         //链表结点类的定义
{
    T data;             //数据域
    LinkNode<T> *link;  //指针域——后继指针
    //仅初始化指针成员的构造函数
    LinkNode(LinkNode<T>* ptr = NULL){ link = ptr; }
    //初始化数据与指针成员的构造函数
    LinkNode(const T& value, LinkNode<T>* ptr = NULL){ data = value; link = ptr; }
};


#endif /* LINK_NODE_H_ */

4.2 栈的的抽象类定义

文件：Stack.h


#ifndef STACK_H_


#define STACK_H_


template <class T>
class Stack
{
public:
    Stack(string name) : m_sName(name){}    //构造函数
    virtual ~Stack(){}                      //析构函数
public:
    virtual void Push(const T& x) = 0;      //新元素x进栈
    virtual bool Pop(T& x) = 0;             //栈顶元素出栈，并将该元素的值保存至x
    virtual bool getTop(T& x) const = 0;    //读取栈顶元素，并将该元素的值保存至x
    virtual bool IsEmpty() const = 0;       //判断栈是否为空
    virtual bool IsFull() const = 0;        //判断栈是否为满
    virtual int getSize() const = 0;        //计算栈中元素个数
    virtual void MakeEmpty() = 0;           //清空栈的内容
private:
    string m_sName;     //栈名
};


#endif /* STACK_H_ */

4.3 链式栈的类定义及其操作的实现

文件：LinkedStack.h


#ifndef LINKED_STACK_H_


#define LINKED_STACK_H_



#include "LinkNode.h"


#include "Stack.h"


template <class T>
class LinkedStack : public Stack<T>
{
public:
    LinkedStack(string name);           //构造函数
    virtual ~LinkedStack();             //析构函数
public:
    virtual void Push(const T& x) ;     //新元素x进栈
    virtual bool Pop(T& x);             //栈顶元素出栈，并将该元素的值保存至x
    virtual bool getTop(T& x) const;    //读取栈顶元素，并将该元素的值保存至x
    virtual bool IsEmpty() const;       //判断栈是否为空
    virtual bool IsFull() const;        //判断栈是否为满
    virtual int getSize() const;        //计算栈中元素个数
    virtual void MakeEmpty();           //清空栈的内容
public:
    string get_name();                  //获取栈名
public:
    template <class T>
    friend ostream& operator<<(ostream& os, const LinkedStack<T>& s);   //输出栈中元素的重载操作<<
private:
    LinkNode<T> *top;   //栈顶指针，即链头指针
    string m_sName;     //栈名
};

//构造函数
template <class T>
LinkedStack<T>::LinkedStack(string name)
: Stack(name), top(NULL), m_sName(name)
{
    cout << "$ 执行构造函数" << endl;
}                       

//析构函数
template <class T>
LinkedStack<T>::~LinkedStack()
{
    cout << "$ 执行析构函数" << endl;
    MakeEmpty();
}   

//新元素x进栈
template <class T>
void LinkedStack<T>::Push(const T& x)
{
    LinkNode<T> *newNode = new LinkNode<T>(x);
    newNode->link = top;
    top = newNode;
}

//栈顶元素出栈，并将该元素的值保存至x
template <class T>
bool LinkedStack<T>::Pop(T& x)
{
    if (true == IsEmpty())
    {
        return false;
    }
    LinkNode<T> *curNode = top;
    top = top->link;
    x = curNode->data;
    delete curNode;
    return true;
}

//读取栈顶元素，并将该元素的值保存至x
template <class T>
bool LinkedStack<T>::getTop(T& x) const
{
    if (true == IsEmpty())
    {
        return false;
    }
    x = top->data;
    return true;
}

//判断栈是否为空
template <class T>
bool LinkedStack<T>::IsEmpty() const
{
    return (NULL == top) ? true : false;
}

//判断栈是否为满
template <class T>
bool LinkedStack<T>::IsFull() const
{
    return false;
}

//计算栈中元素个数
template <class T>
int LinkedStack<T>::getSize() const
{
    int count = 0;
    LinkNode<T> *curNode = top;
    while (NULL != curNode)
    {
        curNode = curNode->link;
        count++;
    }
    return count;
}

//清空栈的内容
template <class T>
void LinkedStack<T>::MakeEmpty()
{
    LinkNode<T> *curNode = NULL;
    while (NULL != top)             //当链表不为空时，删去链表中所有结点
    {
        curNode = top;              //保存被删结点
        top = curNode->link;            //被删结点的下一个结点成为头结点
        delete curNode;                 //从链表上摘下被删结点
    }
}

//获取栈名
template <class T>
string LinkedStack<T>::get_name()
{
    return m_sName;
}

//输出栈中元素的重载操作<<
template <class T>
ostream& operator<<(ostream& os, const LinkedStack<T>& s)
{
    os << "栈中元素个数 = " << s.getSize() << endl;   //输出栈中元素个数
    int i = 0;
    LinkNode<T> *curNode = s.top;
    while (NULL != curNode)
    {
        os << "[" << i++ << "]" << " : " << curNode->data << endl;
        curNode = curNode->link;
    }
    return os;
}


#endif /* LINKED_STACK_H_ */

4.4 主函数(main函数)的实现

文件：main.cpp


#include "LinkedStack.h"


static int total_count = 0;

//判断输入的字符串每个字符是否都是数值0~9
bool IsNumber(const string& s_num)
{
    for (size_t i = 0; i < s_num.size(); i++)
    {
        if ((s_num[i] < '0') || (s_num[i] > '9'))
        {
            return false;
        }
    }
    return true;
}

//输入金盘子个数n
int get_n()
{
    cout << "> 输入金盘子个数，n = ";
    string s_n;
    cin >> s_n;
    while (false == IsNumber(s_n))
    {
        cout << "* 输入有误，请重新输入：";
        cin >> s_n;
    }
    return atoi(s_n.c_str());
}

//构造链式栈
template <class T>
LinkedStack<T>* construct_linkedstack(string name)
{
    cout << "\\n==> 创建链式栈" << endl;
    LinkedStack<T> *linkedStack = new LinkedStack<T>(name);
    return linkedStack;
}

//析构链式栈
template <class T>
void destory_linkedstack(LinkedStack<T>* linkedStack)
{
    cout << "\\n==> 释放链式栈在堆中申请的空间，并将指向该空间的指针变量置为空" << endl;
    delete linkedStack;
    linkedStack = NULL;
}

//初始化汉诺塔的金盘子数
template <class T>
int initialize_Hanoi(LinkedStack<T>* linkedStack_a)
{
    cout << "\\n==> 初始化汉诺塔的金盘子数函数" << endl;
    int n = get_n();
    for (int i = n; i > 0; i--)
    {
        linkedStack_a->Push(i);
    }
    return n;
}

//移动汉诺塔上的金盘子
template <class T>
void Move(LinkedStack<T>* linkedStack_a, LinkedStack<T>* linkedStack_b)
{
    T data;
    linkedStack_a->Pop(data);
    linkedStack_b->Push(data);
    cout << total_count << ": Move top disk from peg" << linkedStack_a->get_name() << " to peg" << linkedStack_b->get_name() << endl;
}

//求解汉诺塔问题
template <class T>
void Hanoi(int n, LinkedStack<T>* linkedStack_a, LinkedStack<T>* linkedStack_b, LinkedStack<T>* linkedStack_c)
{
    if (n == 1)
    {
        total_count++;
        Move(linkedStack_a, linkedStack_c);
    }
    else
    {
        Hanoi(n - 1, linkedStack_a, linkedStack_c, linkedStack_b);
        total_count++;
        Move(linkedStack_a, linkedStack_c);
        Hanoi(n - 1, linkedStack_b, linkedStack_a, linkedStack_c);
    }
}

//输出移动后的汉诺塔的金盘子序号
template <class T>
void putout_Hanoi(LinkedStack<T>* linkedStack_c)
{
    cout << "$ 执行输出移动后的汉诺塔的金盘子序号函数" << endl;
    cout << *linkedStack_c;//或operator<<(cout, *linkedStack_c);
}

int main(int argc, char* argv[])
{
    LinkedStack<int> *Stack_a = construct_linkedstack<int>("A");
    LinkedStack<int> *Stack_b = construct_linkedstack<int>("B");
    LinkedStack<int> *Stack_c = construct_linkedstack<int>("C");
    int n = initialize_Hanoi(Stack_a);
    Hanoi(n, Stack_a, Stack_b, Stack_c);
    putout_Hanoi(Stack_c);
    destory_linkedstack(Stack_a);
    destory_linkedstack(Stack_b);
    destory_linkedstack(Stack_c);
    system("pause");
    return 0;
}

参考文献：
[1]《数据结构(用面向对象方法与C++语言描述)(第2版)》殷人昆——第三章
[2]《C/C++常用算法手册》秦姣华、向旭宇——第十章
[3] 百度搜索关键字：汉诺塔、栈与递归
[4] 汉诺塔小游戏：http://www.4399.com/flash/109504.htm

以上是关于汉诺塔(Tower of Hanoi)问题的求解——利用栈与递归的主要内容，如果未能解决你的问题，请参考以下文章

汉诺塔（Tower of Hanoi）java实现

汉诺塔（Tower of Hanoi）递归代码实现 c语言（顺序栈实现）

汉诺塔问题(The Tower of Hanoi)的递归算法与非递归算法

用递归方法解决汉诺塔问题（Recursion Hanoi Tower Python）

CF392B Tower of Hanoi

Hanoi Tower 汉诺塔问题/c