汉诺塔 （Tower of Hanoi）java实现

Posted 2021-06-11 小写丶H

汉诺塔是典型的递归题的代表，今天就用java语言来实现。

首先，我们是得知道规则，大圆盘必须在小圆盘下面，一次只能一个圆盘。这样我们就可以构思了。

思路：以三个圆盘为例

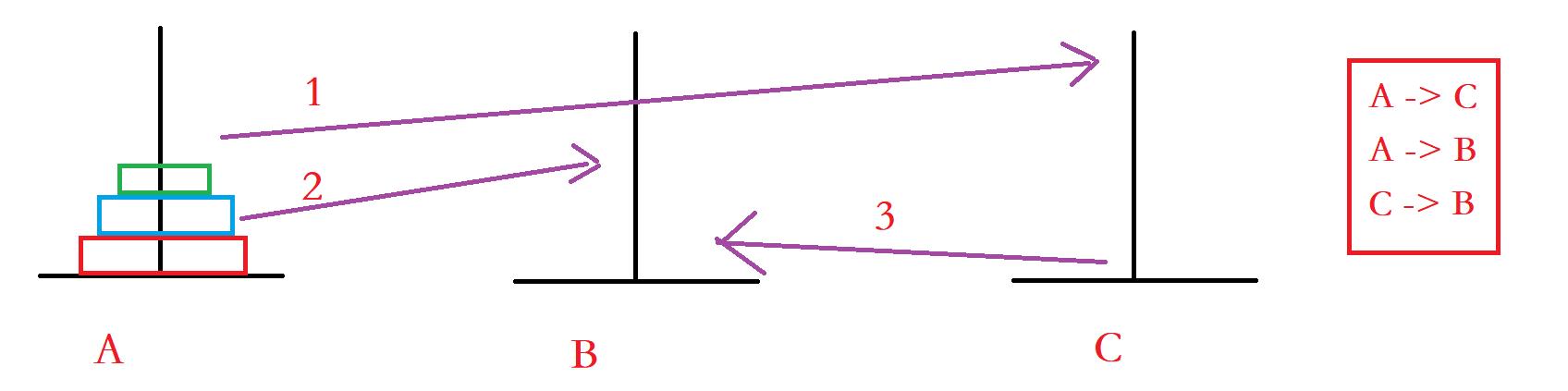
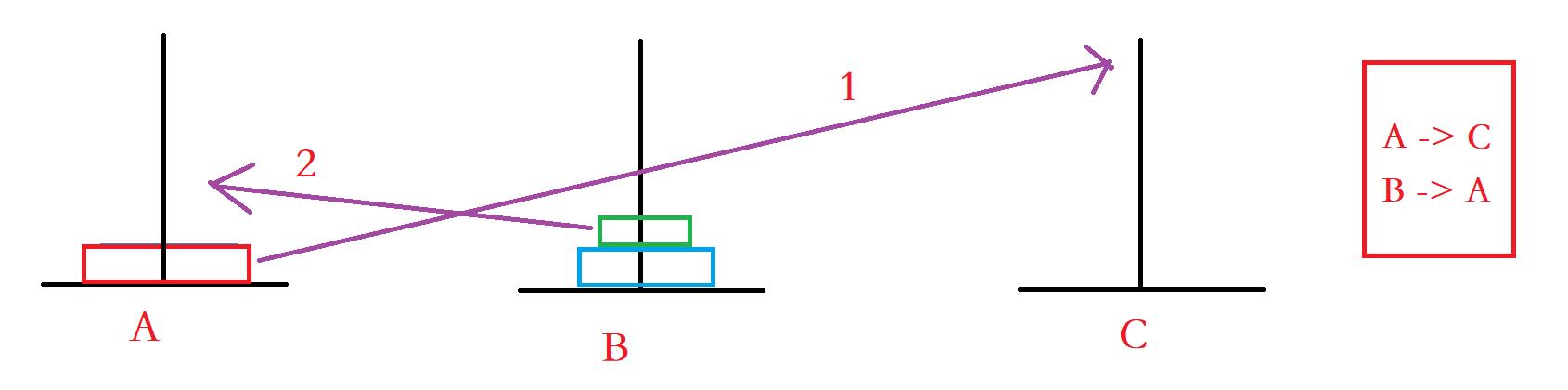
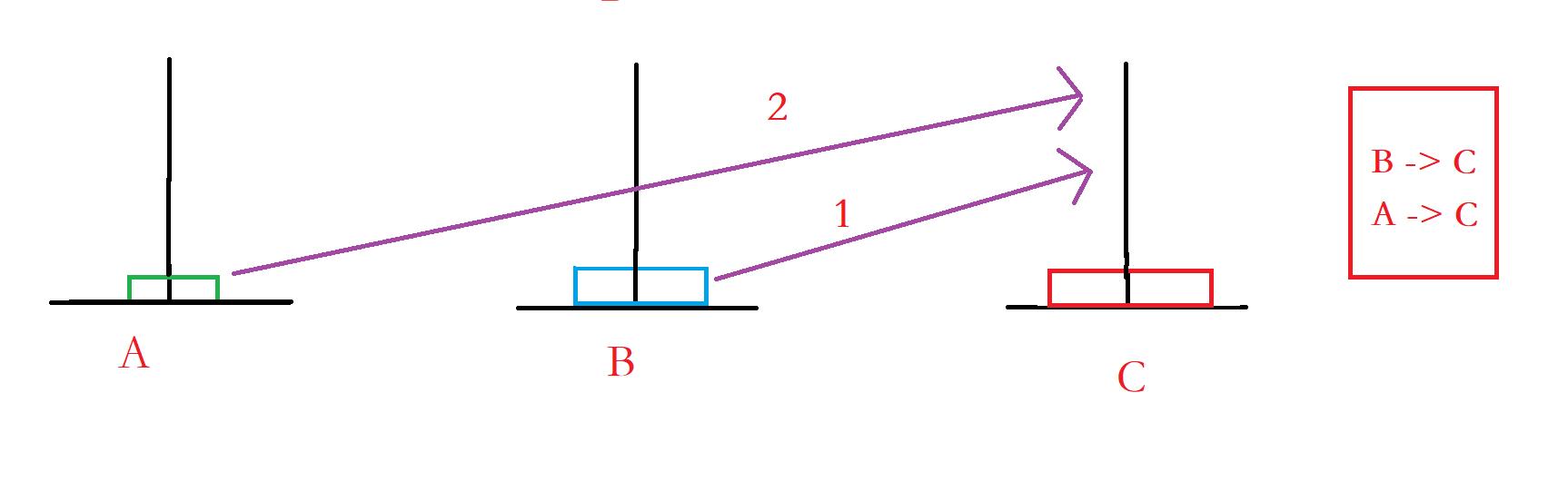
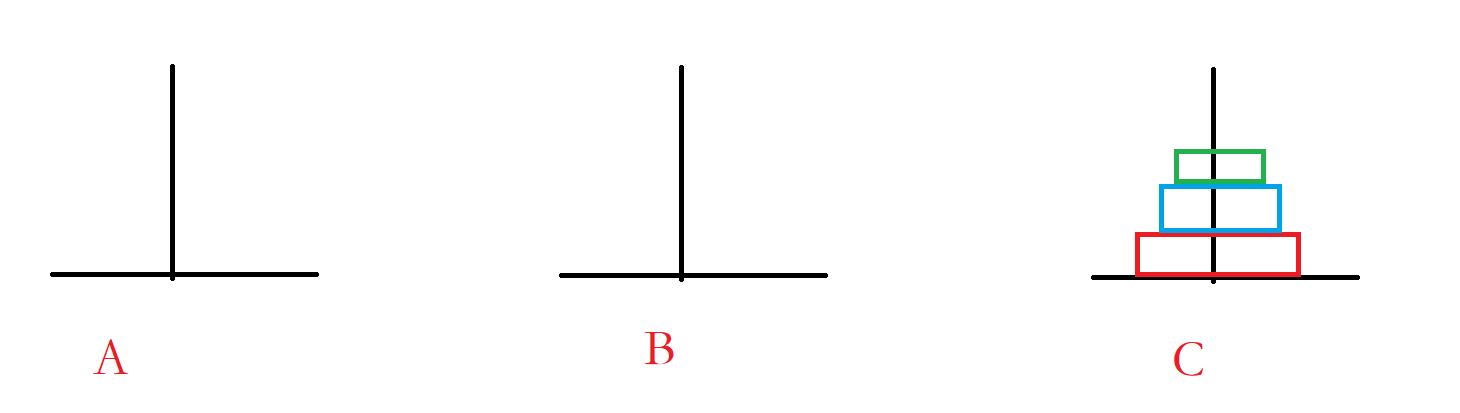
这样就实现了。。

代码实现：

public class Hanoi {
    //从site1移到site2
    public static void move(char site1,char site2){
        System.out.print(site1+" ->"+site2+" ");
    }

    //site1 起始位置
    //site2 中途位置
    //site3 目标位置
    public static void hanoi(int n,char site1,char site2,char site3){

         if(1==n){
             move(site1,site3);
         }else{
             hanoi(n-1,site1,site3,site2);
             move(site1,site3);
             hanoi(n-1,site2,site1,site3);
         }
    }
    public static void main(String[] args) {
        hanoi(1,'A','B','C'); //有一个盘子，
        System.out.println();
        hanoi(2,'A','B','C'); //有两个盘子
        System.out.println();
        hanoi(3,'A','B','C'); //有三个盘子
    }
}

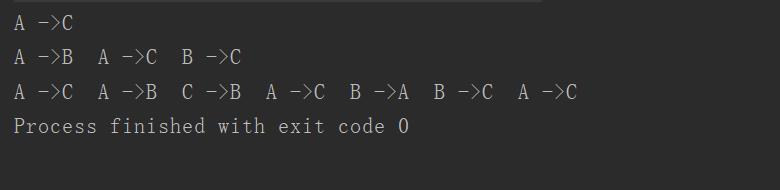
这里提醒，千万不要想着把这个递归函数展开，否则非常复杂，当只有一个圆盘，需要移 1次； 两个，需要移 3次；三个，需要移动7次； 也就是，有n的圆盘，需要移动（2^n）-1。
所以，当n=64时，可想而知，假如每秒钟移动一次，共需多长时间呢？一个平年365天有31536000 秒，闰年366天有31622400秒，平均每年31556952秒，计算一下：18446744073709551615秒。
这表明移完这些金片需要5845.54亿年以上，而地球存在至今不过45亿年，太阳系的预期寿命据说也就是数百亿年。真的过了5845.54亿年，不说太阳系和银河系，至少地球上的一切生命都早已经灰飞烟灭。
温馨提示：
递归思想，只要我们推出公式就好了，不要太过于执着展开。