学习笔记卷积神经网络

Posted 2020-10-30 JasonWood

一、卷积神经网络的应用场景

       卷积神经网络(Convolutional Neural Networks, ConvNets or CNNs)是一种在图像识别与分类领域被证明特别有效的神经网络。

       卷积网络已经成功地识别人脸、物体、交通标志，应用在机器人和无人车等载具。

 

二、卷积神经网络的特点

       使用CNN进行特征提取，优点就是使用者完全不用关心具体的特征是哪些，即实现了特征提取的封装。
       较全连接的神经网络，卷积神经网络计算次数降低很多。

       反向传播法使滤波器可以自动调整，多次训练使误差梯度下降，最终达到想要的效果。具体反向传播法，后面进行说明。

       权值共享：卷积核或者特征滤波器即特征权值，和原始图像卷积，一副图像的所有神经元会共享此一特征权值。

       局部感知：图像的局部特征不会因为其他处变化而对最终得到的特征映射发生变化。

 

三、卷积神经网络的基本结构

      输入层 -->  卷积层 --> 激励函数relu -->  池化层 -->  全连接层 --> 输出层

      INPUT  -->  [[CONV -> RELU]*N -> POOL]*M  --> [FC -> RELU]*K 或FC

      1、输入层：

      首先图像数据转换成矩阵像素数据输入到卷积神经网络中，这一层可以做一些预处理操作，

      有2种常见的图像数据处理方式：

      1）去均值：把输入数据各个维度都中心化到0，也就是算出所有样本的平均值，再让所有样本减去这个均值（CNN在图像上的处理往往只有去均值。）

      2）归一化：幅度归一化到同样的范围，比如把样本都压缩到0~1之间，加快训练网络的收敛性；

      (1)线性函数转换，表达式如下：y=(x-MinValue)/(MaxValue-MinValue) 说明：x、y分别为转换前、后的值，MaxValue、MinValue分别为样本的最大值和最小值。
      (2)对数函数转换，表达式如下：y=log10(x) 说明：以10为底的对数函数转换。
      (3)反余切函数转换，表达式如下：y=atan(x)*2/PI
     

     

     2、卷积层

     卷积层做的就是进行卷积计算，将滤波器或卷积核与原始图像的像素做卷积计算，得到新的特征映射矩阵；

     计算方法就是将卷积核按一定的步长扫描目标矩阵，每扫描到一个矩阵将其内所有对应元素做乘加计算，完整扫描后形成新的矩阵；

     如下图所示：

    

     

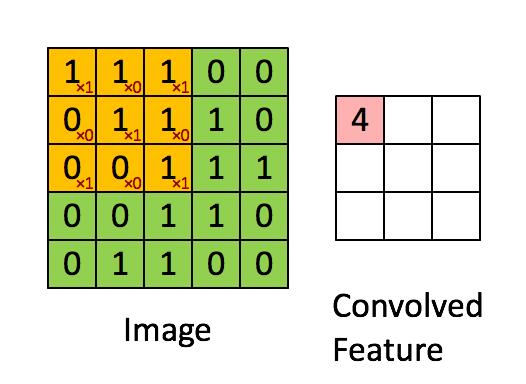
      卷积后矩阵尺寸计算：

      feature_map尺寸计算公式：[ (原图片尺寸 -卷积核尺寸)/ 步长 ] + 1

      卷积层可能会存在多个卷积核，需要分别对每个卷积核做卷积计算生成新的特征映射。

      3、激励函数
      把卷积输出结果做非线性映射，

      常用激励函数：

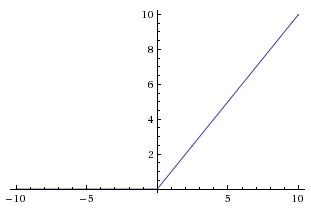
      ReLU：比价常用的激励函数，它有收敛快，求梯度简单，较脆弱这些特点，较脆弱的原因是，当x的值小于0后，它任然会出现梯度为0 的结果。

     

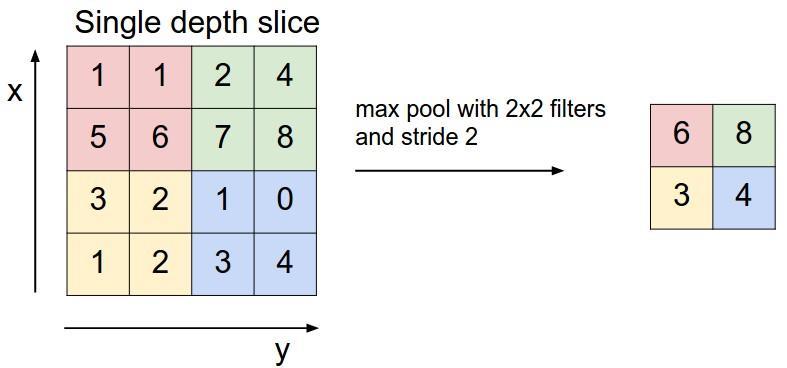
       4、池化层

       它的位置一般是夹在连续的卷积层中间，作用是压缩数据和参数的量，减小过拟合

      

      5、全连接层

      两层之间所有神经元都有权重连接，通常全连接层在卷积神经网络尾部。业界人解释放一个FC layer的主要目的是最大可能的利用现在经过窗口滑动和池化后保留下的少量的信息还原原来的输入信息

      拉直化处理矩阵后，经过softmax函数计算其分类概率。

 

四、卷积神经网络中的反向传播法 （此章节转载：http://www.cnblogs.com/charlotte77/p/5629865.html）

       反向传播法是卷积神经网络最为关键的一个环节，它使得卷积神经网络可以自动化调整卷积核的参数，最终使得准确性达到最大值；

       那么反向传播法是什么呢？

      1）首先计算出当前输出层softmax计算结果和目标结果产生的误差值：

    

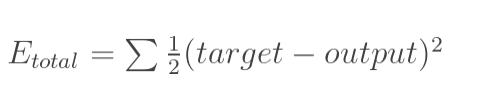
       此处输出层有几个输出，将输出进行均方差后求和。

       2）

以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）

 

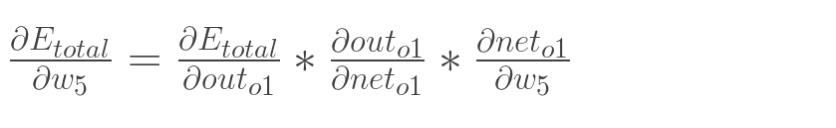
下面的图可以更直观的看清楚误差是怎样反向传播的：

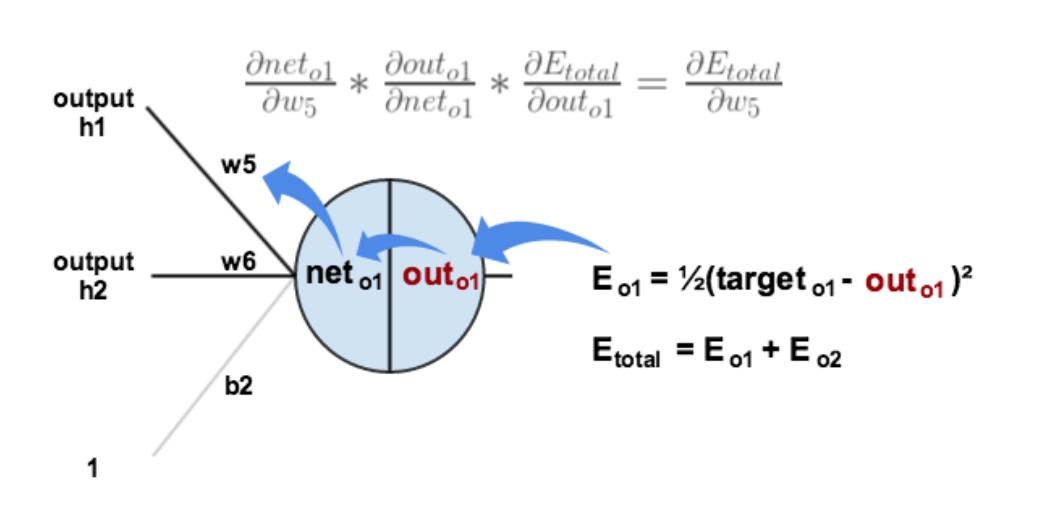
现在我们来分别计算每个式子的值：

计算：

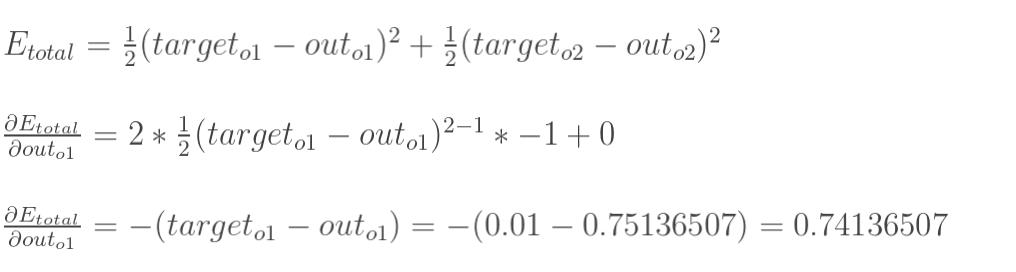
计算：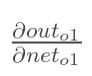

（这一步实际上就是对sigmoid函数求导，比较简单，可以自己推导一下）

 

计算：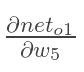

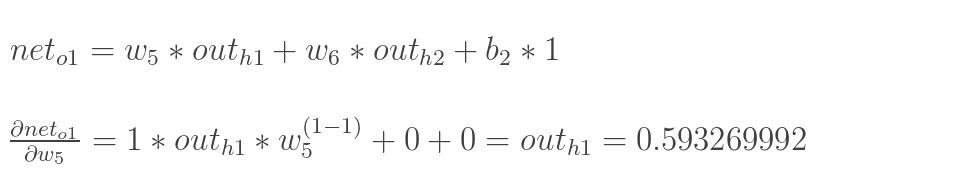
最后三者相乘：

这样我们就计算出整体误差E(total)对w5的偏导值。

回过头来再看看上面的公式，我们发现：

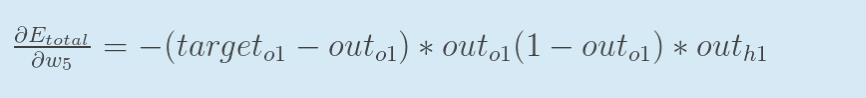
为了表达方便，用来表示输出层的误差：

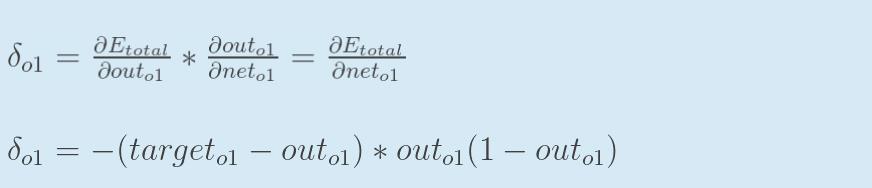
因此，整体误差E(total)对w5的偏导公式可以写成：

如果输出层误差计为负的话，也可以写成：

最后我们来更新w5的值：

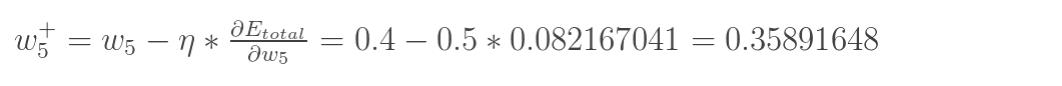
（其中，是学习速率，这里我们取0.5）

同理，可更新w6,w7,w8:

 

 参考文档：

<An Intuitive Explanation of Convolutional Neural Networks>

https://jizhi.im/blog/post/intuitive_explanation_cnn

<一文弄懂神经网络中的反向传播法>

http://www.cnblogs.com/charlotte77/p/5629865.html