深度学习入门-1透彻理解卷积的三层含义:从“卷积”到“图像卷积操作”再到“卷积神经网络”的含义(学习笔记)
Posted 番茄炒狼桃
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习入门-1透彻理解卷积的三层含义:从“卷积”到“图像卷积操作”再到“卷积神经网络”的含义(学习笔记)相关的知识,希望对你有一定的参考价值。
一.写在前面
笔者在进行卷积神经网络入门的时候花了很多功夫,理解的也不够透彻,基础不牢,地动山摇。在查阅了很多资料后,发现了大佬up“王木头学科学”讲的卷积神经网络的理解,茅塞顿开,故此总结了一份王老师的视频笔记,供大家一起交流学习,欢迎指正。
今后还会给持续更新深度学习入门笔记。
全篇多图预警,总计近7500字,记录的也比较仔细,希望能够帮助到各位!
二.正文
(1)卷积的第一层含义:计算系统存量
卷积公式如下,一看到是不是有点懵逼了?
如图1:如果忘记或者没学过高等数学,我们要怎么理解呢?

我们暂且先不去过多地理解这个公式,我们一步一步来,先理解“卷积”这个名字的由来
下面进行举例帮助大家更进一步理解卷积:(例子来源于up主:小元老师高数线代数概率)
小明同学特别喜欢吃东西,除了一日三餐以外,平时还总吃零食,24小时不间断一直在吃。如图2,如果我们用坐标轴表示小明随着时间的推移对应的进食量,那么横坐标是进食时间t,纵坐标代表的是进食量f(t)。

与此同时,他在吃的时候,肠胃还会进行消化,这个消化的情况自然和他吃多少是没有关系的,他吃进去多少,最后都是需要消化的,即:肠胃消化的速率可以看成与小明同学吃的东西没有关系。
因此,我们用坐标轴表示,同样的横坐标表示消化的时间,随着时间的推移,肠胃会对食物进行消化,那么纵坐标表示则对应时间内的食物剩余量。
无论小明在什么时间吃,对应的消化比例都是满足如下图3所示的样子,随着时间的推移,对应之前吃进去的食物消化的就越多,如图也就是小明同学吃的食物到某个时间胃还剩余的量

现在问:下午两点(某个具体的时间点),小明的肚子里还剩下多少食物?
这个问题有几个难点:
- 小明一直在不停地吃,进食量一直在变化
- 小明的肠胃也一直在消化,吃进去的食物在一段时间后会被消化掉
也就是,进食量和消化量都在变化
这样的计算是比较麻烦的。
这个时候,我们利用卷积公式求解,立马就可以解决这个问题,同时如果我们能够按照图表去理解,就能了解卷积的初步含义
我们先看公式,卷积的公式有两个函数,f函数和g函数

用f函数表示进食情况,用g函数表示消化,只要这么代入计算便可求解问题
但它的具体含义是什么呢?
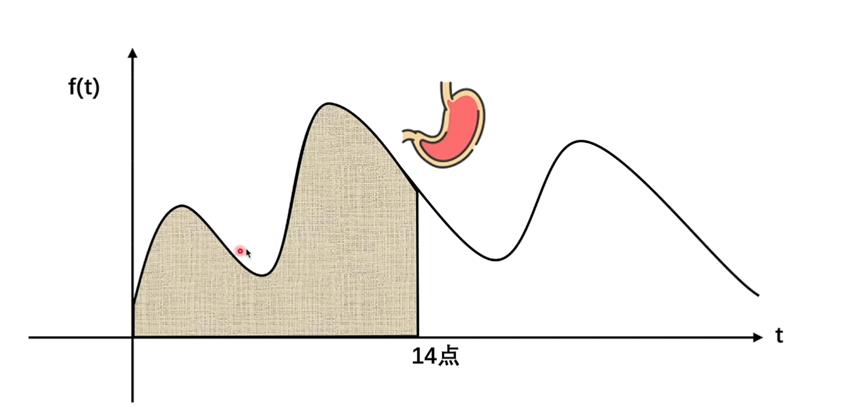
如图5,我们先假设吃的东西不消化(忽略消化),我们把小明同学在14点前吃的所有食物加起来,那就是胃里还剩下的东西(也就是阴影部分的面积)
现在的问题是,如下图6,吃到的食物还在一直消化,随着时间的推移,比如中午12点吃的东西(米饭)到下午14点会不断地进行消化,该食物在胃里的剩余量在下午14点剩下的只有一小部分了。

此时还需要看g函数,代表着消化了多少,即消化量(此处默认每种食物在胃里各个时段的消化量是相同的)
比如现在要知道,在12点吃的米饭到14点胃里还剩下多少,也就是2小时的时间消化了多少,此时需要看g函数

图7上所表述的点,则表示的0开始这是刚吃下去还有百分之百的食物(12点),经过两个小时之后(14点)就可以到虚线部分,表述有一部分食物被消化了。
而图7上虚线对应的点,其实就是表示的此时胃里还剩的食物有多少(胃里对应时刻的米饭剩余量),当然就是一个百分比(比率),所以说具体剩的这个数值呢,肯定是最开始吃到那个食物,再乘以(14-12)=2也就是两小时候这碗米饭还能剩下多少比例(12点时的食用量×下午14点时剩余的比例,即f(12)*g(14-12))。
但是小明同学是在持续不断地进食的,假设他在上午10点吃了一个面包,10点到下午14点总共14-10=4小时,此时要计算面包在14点的时候在胃里的剩余量,那就需要f(10)*g(14-10),也就是10点对应面包的进食量×14点时面包在胃里对应的消化后剩余的百分比(如下图8,右边部分对应的是胃里在14点时各个食物的剩余量)。
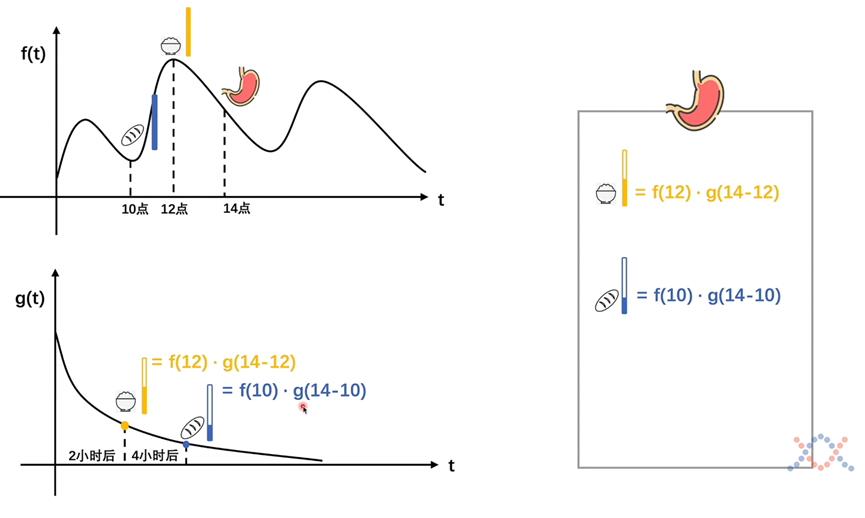
因此,也是说在下午两点,胃里同时有米饭剩下的部分以及面包剩下的部分。
那如果说还有第三个点,比如说在早上8点的时候小明吃了两碗豆腐脑,在下午2点的时候还剩下多少呢,那么就是如图9绿色的部分,同理,剩下的量为f(8)*g(14-8)。
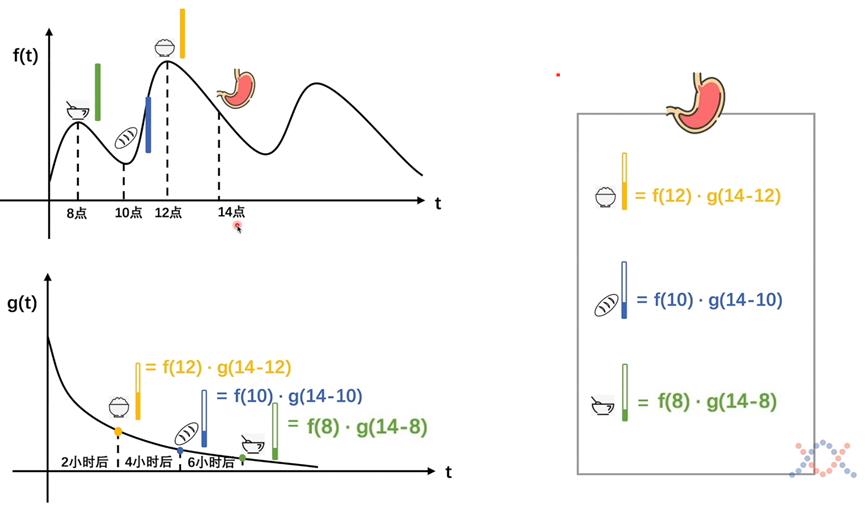
此时胃里在下午14点剩下的东西则为米饭剩余量+面包剩余量+豆腐脑剩余量。
那么整个加起来就是下午两点胃底总共还剩的食物了。
更加普遍的情况(推广),如果我们现在要求的是t时刻胃里还剩多少东西,那其实就是要把小明在t时刻之前,对应的每一个时间吃的食物的剩余量分别算出来,在进行相加。
如图10,比如问从x时刻吃的食物到了t时刻还剩下多少,那么我们首先计算t到x时刻吃的食物经过的时间,那就是t-x,然后用x时刻的进食量乘以t-x后对应的剩余比例

当然这只是看一个点了,我们的目的呢,还是要看t时刻前面所有时刻,每一个点到了t时刻还能剩下多少,也就是需要把t时刻之前所有吃的食物的剩余量算出来相加在一起,即可计算出胃里在t时刻时的食物剩余量
那这个过程呢,其实就是一个积分过程。
写出来的话就是以0为下限,t为上限,对这个函数求一个定积分,最后计算出来的结果那就是在t时刻胃里的食物剩余量。
Tip:观察两个函数中的两个变量相加之后(x和t-x),能不能消掉其中一个未知数,若能消掉,则为卷积,这其实也是判断这是不是卷积的一个重要标志
(此处的x被消掉了,因此可以通过此方法来判断这是个卷积)

那么,x和t-x在图像上对应的表示是什么呢?
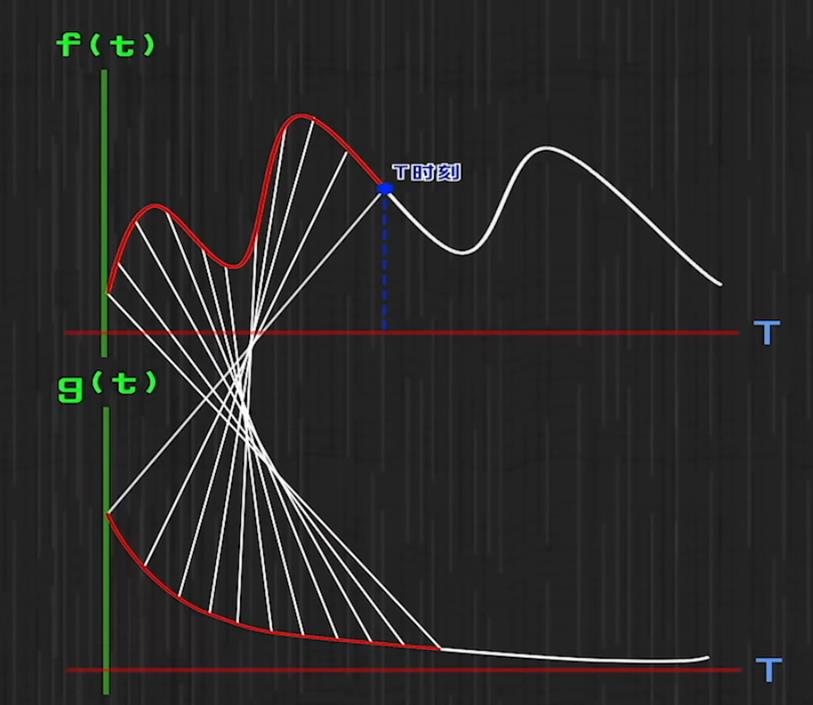
如图12所示,x和t-x对应的应该是f函数到g函数的一条连线

如图12,T时刻的时候小明刚刚吃进去的食物还没有消化,所以说这个点对应到g函数上就是g(0),可以理解成食物还没开始消化。
同样的道理,如图13,T时刻前的对应每一种食物的在T时刻时的剩余比例,都是一条直线一一对应。
这句话有点绕,其实也就是你在x时刻(x<=t)吃的食物,在t时刻的剩余比例其实对应的就是g(t-x)

因此,每一条直线,都意味着,一对f(x)与g(t-x)相乘,最后只要把所有的值都加起来,这就是我们要求的胃里的食物剩余量。
于是我们就可以得到图14这样一个式子了:

红色框里的式子除了上下限和变量符号不一样,其他的都是一样的。此处变量的符号本质上可以根据需要直接替换(效果相同),然后此处考虑的时间不同,所以对应的积分上下限也不一样,因此不少正无穷到负无穷。
因此,可以总结一下卷积的含义:
一个系统满足:
- 输入不稳定
- 输出稳定
那么我们就可以用卷积求系统的存量
此处的输入f函数是指每个时刻吃的食物的进食量是不一样的;
输出是指g函数是固定的(每种食物到胃里随着时间的推移对应的剩余比例是一样的),即系统的流出是固定的。
现在又有一个问题,那就是卷积,
为什么叫卷积呢?卷在哪了呢?
如图15,其实还是相对而言比较别扭的
如图16,如果我们把g函数反转以后,就豁然开朗了

把g函数翻转和平移了一下,所以叫卷积
那么进入下一个环节,“卷积神经网络”
(2)卷积的第二层含义:图像处理
卷积神经网络主要用途就是识别图片里的内容,比如把图片里的猫挑选出来(图像分类)
那它之所以叫卷基神经网络就是因为在把图片交给神经网络之前,先要对图像进行一个卷积操作。
现在我们来理解图像的卷积操作。
如果直接去看图像,会发现我们之前所学习的f函数和g函数无法进行很好地理解和对应。
电脑里的图片,例如图17,可以当成一个一个像素点组成的(类比成一个表格),表格的信息包含像素点、灰度值、RGB值等

什么是卷积操作呢?
就是用一个3×3的点阵和图像进行一个操作,那这个3×3的点阵呢就被叫做卷积核
如下面的视频片段所示,操作的过程是把卷积核扣在图像的点阵上,然后对应的两个格子相乘,3x3的点阵应该是有九个数相乘,最后还要把这个九个相乘的数的结果相加保存到一起,这就相当于得到了一个新的像素点(是不是类似于先计算对应每个食物的剩余量,再相加即可得到某一时刻胃里剩余的食物量)
图像卷积操作过程
图像原本的像素点先和对应的卷积核相乘后再相加,即可得到对应新的像素点。
接下来,只需要用卷积核把整个图像都扫一遍,得到的就是卷积操作后的新图像了。
对于最外层没扫到的那一圈,只需要在处理之前,给图像外面加一圈都是零的像素,最后就能得到一个同样大小的图片了。
下面的图片就是对图像进行卷积操作后的结果,可以看到刚才那些计算还比较简单,没有积分什么的复杂运算

但是这个和卷积的关系在哪呢?哪个是f函数哪个是g函数呢?
更好的理解方式
图像的卷积操作就是拿图片和卷积核,相乘再相加,类似于下图的卷积计算

因此,图像和卷积核一个是f函数一个是g函数。
答案是,图像是f函数,卷积核是g函数
因为图像里的像素点总在变化,对应系统的不稳定输入,
而卷积核的数值确定了以后就不会再改变,对应的是稳定输出。
如图20,现在我们已经从吃东西的一维问题,变成了如图的二维问题,不能相提并论

看到这可能就开始懵逼了,这个很难理解,我们换别的方法来理解。
到底卷积核和图像像素点有什么关系呢?
我们必须重新理解卷积到底是什么,这样才能彻底明卷积图像的操作背后的意义。
毕竟一个图像,它不是一个系统,它没有稳定的输入,也没有稳定的输出。
之前的理解可能把卷积理解的狭隘了,现在我们就来。来深挖一下刚才吃饭的那个例子了。
我们刚才吃饭的这个例子,其实是相当于把吃东西看作对系统的输入,消化看作是系统的输出,而最后胃里还剩的东西就是系统里的存量。

如果只是盯着这一个例子去看的话,那我们其实很难跳出来去对他有一个更广泛的理解,把这个例子换一下:
如下图22,如果是在t时刻发生了飓风,而发生飓风的原因是在此之前有很多蝴蝶煽动了翅膀,
比如说在x时刻有只蝴蝶在猛烈地煽动翅膀,
而蝴蝶煽动翅膀这件事会对t时刻发生飓风产生影响,
但是这个影响它是会随着时间的变化而发生变化的,
那它的影响力的变化则需要看g函数(煽动翅膀随着时间的变化影响力逐渐衰减)
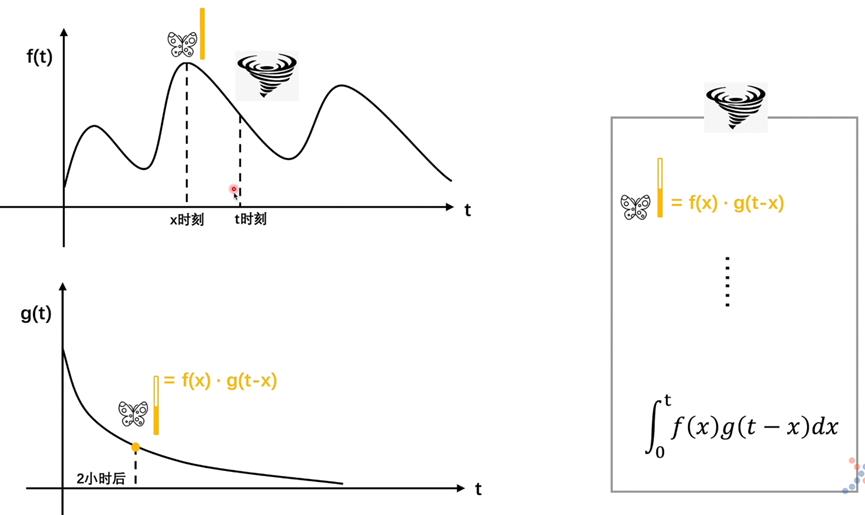
此时卷积则表示的是某时刻飓风发生的时候和之前蝴蝶扇动翅膀对自己产生了多少影响。
所以我们可以总结一下,卷积可以看成:
计算众多事件对某时刻发生的事情的影响值。
即在某一个时刻发生了一件事,而这件事的产生会受到之前发生很多事的影响的。
也就是在x的时刻他发生了一件事,这件事会对t时刻产生影响,具体怎么影响呢,还要看从x的时刻到t时刻经历的时间,影响力会随着时间进行变化
而规定随时间如何变化的,就是g函数,g函数就规定了之前发生的一些事情随着时间影响力是如何变化的。
TIP:之前小明吃饭的例子还是这个蝴蝶煽动翅膀,它的影响力都是随着时间减小的,但也会存在影响力随着时间变化而增大的情况。
回到图像的卷积操作,类比一下在图像上进行卷积操作,可以看成计算很多个像素点,对某一个像素点是如何产生影响的。
这个3×3的点阵就(卷积核)的数字不一样,最后处理的图像的效果也是不一样的。
如下图23的卷积核,本质上是找到一个像素点,然后把它周围的像素点全部加起来

这个卷积核它本质上呢其实就是找一个像素点,把它周围的像素点全部加起来,然后求平均。 这样处理完的图像,它的效果可让图像变得更平滑、更朦胧,叫做平滑卷积操作。
如图24是平滑卷积操作后的效果

什么是平滑操作呢?
其实就是让周围的像素点和当前的像素点相差不要太大,刚才那个卷积核我们可以看到它是在求平均值(平均值就是看到周围的像素点和目标像素点相比,判断这个像素点的数值是不是太高了,如果太高了,就拉低点,如果太低了,那就拉高一点)
卷积核就容易理解了,其实就是规定了周围的像素点是如何对当前像素点产生影响的。
对于3×3的卷积核来说,它其实就是规定的周围一圈像素点对当前像素点产生的影响。
类似的还有5×5的卷积核以及7×7的卷积核,也就是周围两圈像素点和三圈像素点对当前像素点产生的影响。
从数学上来看,应该是可以规定从无限远处对当前像素点产生的影响。
而前面的小明吃饭的举例,它也是规定了当前时刻的之前的每一个时刻对当前的影响(好拗口),也就是规定了选定时刻受到之前每一个时间点的影响。
不过对于计算机领域来说,一般考虑到性价比不会让卷积核太大。
现在我们来更深入地去了解一下,从卷积核的数学运算的角度去理解

如图25,其中f(x,y)*g(x,y)表示的是卷积操作,等号后面的g函数和f函数的未知数相加以后剩下m和n,那么就是卷积(而此处使用了累加符号是因为考虑的是像素点,并不是连续的,所以不使用积分)
如图26,现在考虑(x,y)相邻的1个像素点的影响就如上图所示(只需要标注一圈)
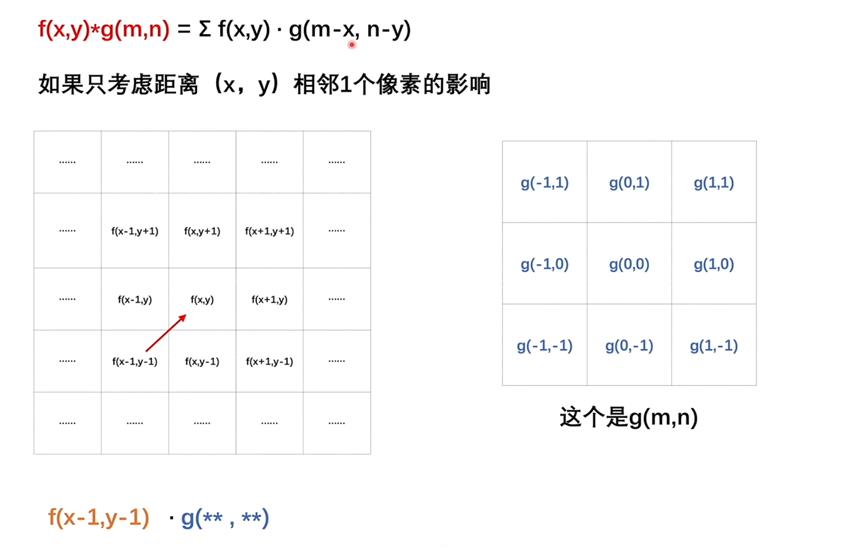
现在我们需要考虑(x-1,y-1)的像素点对选定的像素点(x,y)的影响,那我们应该找到他对应的像素值f(x-1,y-1),再乘上其对应的影响比例,即g函数中的值,这个具体是哪个值则需要一些转换。
如下图,我们现在假设(x-1,y-1)是x时刻,而(x,y)是t时刻。
在小明吃饭的例子中,我们要考虑的就是t时刻之前所有的时间对t时刻发生的事情产生的影响,现在呢,我们其实就是相当于在考虑,周围的像素点对这个像素点产生的影响。
需要具体到这个像素点的时候,我们就可以把它想象成是x时刻,
之前小明吃饭的例子是需要用t-x,而此处类比过来则是x-(x-1)以及y-(y-1),那么对应的g(1,1)
同理,如果把所有的点对应的g函数的情况都计算出来,则如图27
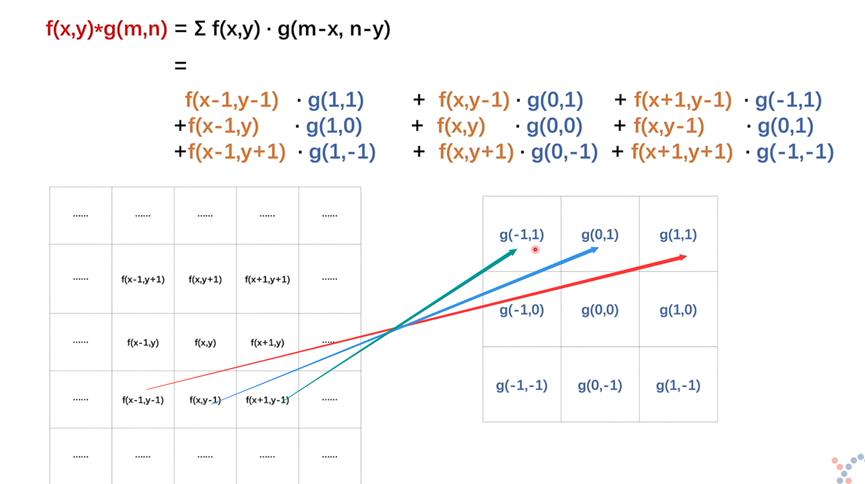
其实可以根据箭头的对应关系看出,还是f函数和g函数的一一对应关系还是比较难看的
此时,如图28,我们只需要对g函数的图像旋转180°,就会很清晰了

此时每一个点都是一一对应的关系了,这个翻转是不是有类似于“卷积”中的“卷”的含义呢。

因此,总结一下,如图29所示,下面的g函数的图像需要翻转180度后才是一一对应关系,才是我们的卷积核,卷积核是可以扣在图像上的,直接相乘再相加即可,本质上还是一个卷积运算。
现在,从卷积到图像的卷积操作,都讲清楚了。
其中的关键就是要把卷积当作是过去对现在的影响,
也就是周围像素点对当前像素点的影响或者是之前所进食的食物对现在胃剩余食物量的影响,
还可以是之前蝴蝶扇动的翅膀对现在产生飓风的影响。
而g函数,则规定的是如何影响的。
(3)卷积的第三层含义:过滤器
现在我们来到第三步骤,卷积神经网络的第一层的作用及其与卷积的关系。
(此处参考了Up主同济子豪兄的视频)
卷积神经网络一般是用来做图像识别的。
如图30中所示,输入图片里面的有X有O,通过卷机神经网络就能识别出来它们是X和O

如图31,重点的不是识别这种规规整整的情况,而是形如下图31这类不规整的情况下的x和o,这种情况我们人是能一眼就看出来的,而计算机是不能直接识别的。

计算机不能识别出来,因为计算机看到的都是下图32的情况,像素点都是数字(此处把问题解化了,一个像素就有两种情况,1和-1)

如果我们把下图33的像素点进行挨个比较,那计算机会识别出两个图片是完全不一样的

自然给计算机识别后会得到下面图34的结果

但我们仔细看的话可以发现,
如下图35两边的图像虽然不同但是如果只看局部的话,局部是有相同地方的,
所以卷积神经网络识别图像的第一步就是把图像的局部特征提取出来
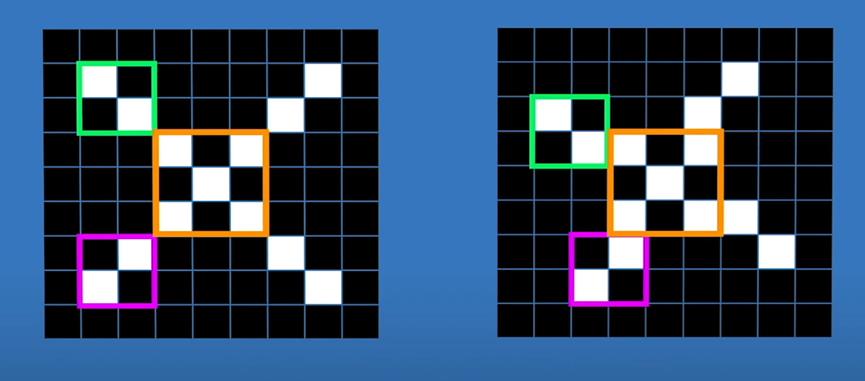
然后把这些局部特征交给神经网络,由神经网络去进行分类判断
现在又有新的疑惑了,要如何提取图像的局部特征呢?
为什么对图像进行卷积操作就是提取图像的局部特征呢?
我们根据之前的介绍知道卷积操作的本质是去处理一个像素点和周围像素点的关系的,处理完的结果应该是和一个原图差不多的图片(平滑操作)。
那到现在卷积还怎能去提取图像的局部特征呢?
这时候就需要拓展更多的卷积核类型,我们之前所说的卷积核只是平滑卷积核,
目的是让图像经过卷积操作后变得更加平滑朦胧。事实上,卷积操作还有很多的卷积核。
如下图36的上b半部分的卷积核,经过该卷积核进行卷积操作的图像,
最后得出的图像里就只把垂直方向的边界给挑选(提取)出来了,忽略了横向边界。

如图37,同样的道理,如果用这个为卷积核进行卷积操作的话,那就会忽略垂直方向的边界,只把左右方向的边界给提取出来。

如图37所示,虽然还是进行的卷积操作,但其实最后的效果是把图片里的一些特征给提取了出来。所以,卷积操作其实还有个功能,如果挑选的卷积和合适,最后就可以对图片进行过滤,把某些特征保存下来 而其他的特征就被过滤掉了。
此时,卷积核被叫做过滤器,上面的两个卷积核分别叫做垂直边界过滤器和水平边界过滤器。
因此,总结下来:
我们可以把图像和卷集合的相乘再相加,看作是周围像素点对当前像素点的影响。
其中这个相乘在相加,还可以看作是自己选的像素点对周围像素点的一个试探。
而那个卷积核就是该选定的像素点的模板,当我们不想考虑某个位置的时候,就可以把它设置成零而,需要重点考虑某个位置的时候,就可以把这个位置的素质设置的比较高。(此处可以看成设置的权重比较大)
总之就是不同的卷积核(模板),可以带来不同的效果
此外,平滑操作可以看成像素进行拟人化之后,被动无奈地接受最后图像的处理效果。
过滤器就是让选定像素点可以进行主动的试探和选择。
所以我就再一次对卷积操作有了一个新的理解
卷积核在图像识别的情况下,就是对周围像素点的主动的试探和选择。
通过卷积核把周围有用的特征给保留了下来。

回到前面识别x的那个问题,利用这三个卷积核就可以把三个特征都给找出来,分别是左上到右下,全是1. 还有x的位置都是1,以及从左下到右上都是1。
如图的情况就是完美匹配
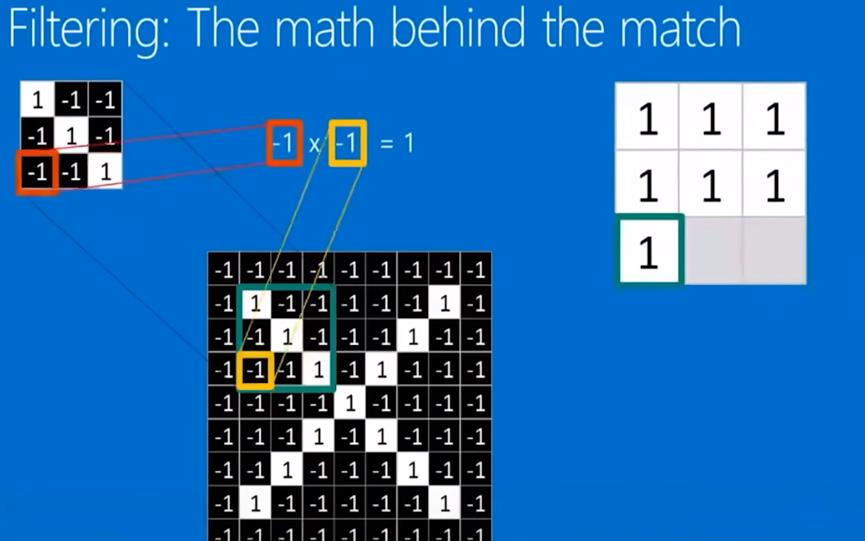
完美匹配的计算结果自然是1

而下图41的情况,虽然不是完美匹配。
最后计算的结果就是0.55。

如图42,将整个图像都进行一次的卷积操作之后,最后就包含了与这个特征匹配的全部信息

如图43,然后再把三个特征的卷积核都分别再进行卷积操作一遍,接下来神经网络就开始干活了。

神经网络通过对这些特征信息的判断就可以进行图像识别了,后续还有池化、反向传播等内容,我们接下来再进行讲解。
三.总结
最后总结一下,
卷积至少有三层含义:
第一层就是吃饭的例子里面一个系统,它有不稳定的输入,有稳定的输出,则可以通过卷积计算系统的存量
第二层就是图像处理,一个卷积核其实就是规定周围像素点对当前像素点会产生怎样的影响。
第三层就是一个过滤器的卷积核,规定了一个像素点会如何试探周围的像素点,以此筛选图像的特征。
不论哪一层,卷积在数学上其实是没有差别的,它们的意义都是相同的,但是利用到不同的地方,这意义就发生了改变。
最后一句话总结:卷积就是瞬时行为持续性后果的总和
四.写在最后
以上就是卷积的三层含义的学习笔记,再次感谢王木头、小元老师以及子豪老师的讲解。
参考文献:
从“卷积”、到“图像卷积操作”、再到“卷积神经网络”,“卷积”意义的3次改变_哔哩哔哩_bilibili
【小动画】彻底理解卷积【超形象】卷的由来,小元老师_哔哩哔哩_bilibili
大家有方便的话可以支持点击上面的链接给各位老师三连!!
以上是关于深度学习入门-1透彻理解卷积的三层含义:从“卷积”到“图像卷积操作”再到“卷积神经网络”的含义(学习笔记)的主要内容,如果未能解决你的问题,请参考以下文章