概率论与数理统计——正态分布

Posted 2020-10-30 你好vinn

指数的负数次方图像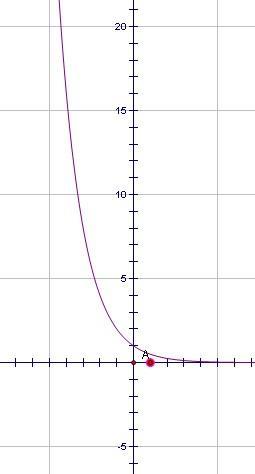

方差：各个数与其平均数之差的平方的平均数：1/5[（1-3）²+（2-3）²+（3-3）²+（4-3）²+（5-3）²]=2

标准差：方差的平方根就是标准差。

分布函数F(x)=P(X<x)，表示随机变量X的值小于x的概率。

概率密度f(x)是X落在x处“单位宽度”内的概率。随机变量X落在(x, x+Δx)内的概率约为f(x)Δx，即P(x<X<x+Δx)≈f(x)Δx。

 

 

正态分布的概率密度函数为：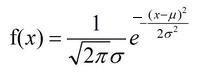    

第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ，σ^2 )。（方差的平方根就是标准差，标准差的平方就是方差）。

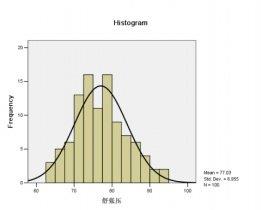
均数μ决定正态曲线的中心位置；标准差σ决定正态曲线的陡峭或扁平程度。σ越小，曲线越陡峭分布越集中在μ附近，；σ越大，曲线越扁平分布越分散。

标准正态曲线N（0，1）是一种特殊的正态分布曲线，标准正态分布的μ和σ^2为0和1。

标准正态曲线中：密度函数关于平均值对称，平均值与它的众数（statistical mode）以及中位数（median）同一数值。关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。

https://www.cnblogs.com/tsingke/p/5866672.html  用c语言 产生服从均匀分布, 瑞利分布，莱斯分布，高斯分布的随机数

                         正态曲线下横轴上一定区间的面积反映该区间的例数占总例数的百分比，或变量值落在该区间的概率。