1.点云分割的精度
在之前的两个章节里介绍了基于采样一致的点云分割和基于临近搜索的点云分割算法。基于采样一致的点云分割算法显然是意识流的,它只能割出大概的点云(可能是杯子的一部分,但杯把儿肯定没分割出来)。基于欧式算法的点云分割面对有牵连的点云就无力了(比如风筝和人,在不用三维形态学去掉中间的线之前,是无法分割风筝和人的)。基于法线等信息的区域生长算法则对平面更有效,没法靠它来分割桌上的碗和杯子。也就是说,上述算法更关注能不能分割,除此之外,我们还需要一个方法来解决分割的“好不好”这个问题。也就是说,有没有哪种方法,可以在一个点不多,一个点不少的情况下,把目标和“其他”分开。
答案是有,也就是这篇博文要解决的最小割算法。
2.最小割算法
最小割(min-cut)并不是一个什么很新鲜的东西。它早就用在网络规划,求解桥问题,图像分割等领域,被移植到点云分割上也不足为奇。最小割算法是图论中的一个概念,其作用是以某种方式,将两个点分开,当然这两个点中间可能是通过无数的点再相连的。如图所示。
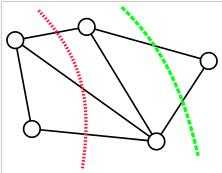
如果要分开最左边的点和最右边的点,红绿两种割法都是可行的,但是红线跨过了三条线,绿线只跨过了两条。单从跨线数量上来论可以得出绿线这种切割方法更优的结论。但假设线上有不同的权值,那么最优切割则和权值有关了。它到底是怎么找到那条绿线的暂且不论。总而言之,就是有那么一个算法,当你给出了点之间的 “图” (广义的),以
3.点云 “图”
显而易见,切割有两个非常重要的因素,第一个是获得点与点之间的拓扑关系,也就是生成一张“图”。第二个是给图中的连线赋予合适的权值。只要这两个要素合适,最小割算法就会办好剩下的事情。点云是一种非常适合分割的对象(我第三次强调这个事情了),点云有天然分开的点。有了点之后,只要把点云中所有的点连起来就可以了。连接算法如下:
1.找到每个点最近的n个点
2.将这n个点和父点连接
3.找到距离最小的两个块(A块中某点与B块中某点距离最小),并连接
4.重复3,直至只剩一个块
现在已经有了“图”,只要给图附上合适的权值,就完成了所有任务。物体分割给人一个直观印象就是属于该物体的点,应该相互之间不会太远。也就是说,可以用点与点之间的欧式距离来构造权值。所有线的权值可映射为线长的函数。
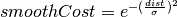
貌似我们现在已经搞定一切了,其实不然。分割总是有一个目标的,而这种精准打击的算法,显然你要告诉我打击对象是谁,打击范围多大——目标需要人为指定(center),尺寸需要提前给出(radius)。
OK,我们现在有了打击对象了(指定了目标物体上的一个点),接下来要做的,就是让除此对象之外的物体被保护起来,不受到打击。保护的方法就是认为加重目标范围之外的权值(罚函数)
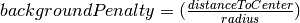
上述过程其实看起来还不够智能,如果有办法让我只需要点一下鼠标,选中要分割的物体,接下来电脑替我操心其他事情,那就太好了。这其实是可以实现的,称为AutoMatic Regime.但PCL并没有封装这个算法,忽略不表。
4.PCL对最小割算法的实现
//生成分割器 pcl::MinCutSegmentation<pcl::PointXYZ> seg; //分割输入分割目标 seg.setInputCloud (cloud); //指定打击目标(目标点) pcl::PointCloud<pcl::PointXYZ>::Ptr foreground_points(new pcl::PointCloud<pcl::PointXYZ> ()); pcl::PointXYZ point; point.x = 68.97; point.y = -18.55; point.z = 0.57; foreground_points->points.push_back(point); seg.setForegroundPoints (foreground_points); //指定权函数sigma seg.setSigma (0.25); //物体大概范围 seg.setRadius (3.0433856); //用多少生成图 seg.setNumberOfNeighbours (14); //和目标点相连点的权值(至少有14个) seg.setSourceWeight (0.8); //分割结果 std::vector <pcl::PointIndices> clusters; seg.extract (clusters);
显然,最小割算法更注重分割的精确性而不是分割自动进行。最小割算法用于半自动分割识别有着巨大的优势,适合用于计算机视觉,城市场景点云分析一类。但对机器人来说,或许和特征点检测算法联合起来能获得较好的效果

图中显示,最小割算法成功找到了靠的很近的汽车。显然欧式算法r取太大则无法区分左右汽车,r取太小则无法区分车头和车身(玻璃不反光,是没有点云的)。