回溯算法入门及经典案例剖析(初学者必备宝典)
Posted Angel_Kitty
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了回溯算法入门及经典案例剖析(初学者必备宝典)相关的知识，希望对你有一定的参考价值。
前言
基于有需必写的原则，并且当前这个目录下的文章数量为0(都是因为我懒QAQ)，作为开局第一篇文章，为初学者的入门文章，自然要把该说明的东西说明清楚，于是。。。我整理了如下这篇文章，作者水平有限，有不足之处还望大家多多指出~~~
概念
首先，回溯是什么意思？很多初学者都会问这样的一个问题。我们可以举这样一个例子：
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
我们看到了如图所示的一个4*4的迷宫了，我们假设数字1标记的位置为道路，数字0标记的位置为一堵墙，一个人由起点(0.0)走到终点(3,3)，我们有几种方式可以到达呢？这个是不是很简单的一个问题，由图我们可以推出有两种方式可以到达，并且每条路径的长度均为6(设单位长度为1)。
众曰：诶，樱姐姐，你说的这个问题和我们将要提的有关系嘛？似乎你并没有提到回溯这个概念啊！！！
樱姐姐：当然有关系啦！继续往下看，假如我们把终点由(3,3)换成(1,3)，结果是不是会有变化呢？
我们由图中可以看出有两条可以到达的路径：(0.0)->(0,1)->(0,2)->(0,3)->(1,3)，(0,0)->(0,1)->(1,1)->(2,1)->(3,1)->(3,2)->(3,3)->(2,3)->(1,3)
两条路径长度分别为4和8(设单位长度为1)，并且我们可以知道由起点到终点的最短的路径为(0.0)->(0,1)->(0,2)->(0,3)->(1,3)，长度为4
如果把这一过程交给计算机来处理，计算机该怎么办呢？
此时就要提到我们这个伟大的回溯算法啦！！！
首先回溯算法类似枚举的搜索尝试过程，何为枚举，可参考之前写过的一篇文章，我们需要在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。
比如，我们要从(1,1)这点出发，找到(3,3)这个位置，计算机所计算出的可能路径就不是简单的两条了，因为在我们所到达的每一个点，都有上下左右四个方向可以走，而计算机只能去执行我们所设定的参数变量去搜寻可以行走的路线，我们就需要去进行一个设计线路，让人能从这个迷宫里走出来，一旦发现这条路不通(遇到了墙)，就要退回上一步进行重新选择，这种走不通就退回再走的方法称为回溯法。
说到这里相信大家都差不多理解了回溯法的概念，个人理解，如果对DFS(Depth-First-Search)和BFS(Breadth-First-Search)有了解的同学对回溯这个概念应该是再熟悉不过了，因为实质就是在问题的解空间进行深度优先搜索。DFS是个图的算法，但是回溯算法的图在哪里呢？我们把解空间的一个状态当做一个节点，由于解空间非常庞大，这个图就大到无法想象了。
为了能够撤销当前的求解过程，必须保存上一步以来的求解路径，这一点相当重要。
对DFS和BFS不了解的同学，请转到传送门：这里哦！
解题步骤
- 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
- 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
- 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。
一般写法：
1 void search(){ 2 //回溯条件 3 if(满足条件){ 4 return; 5 } 6 //否则继续进行搜索 7 ...... 8 }
实例分析
1.八皇后问题
该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。
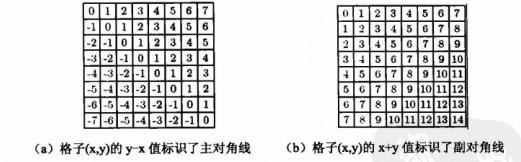
如果我们逐行放置皇后则肯定没有任意两个皇后位于同一行，只需要判断列和对角线即可。使用一个二维数组vis[3][]，其中vis[0][i]表示列，vis[1][i]和vis[2][i]表示对角线。因为(x,y)的y-x值标识了主对角线，x+y值标识了副对角线。由于y-x可能为负，所以存取时要加上n。
参考写法如下：
1 void search(int cur) 2 { 3 int i,j; 4 if(cur==8) tot++; 5 else 6 { 7 for(i=0;i<8;i++) 8 { 9 if(!vis[0][i]&&!vis[1][cur-i+8]&&!vis[2][cur+i]) 10 { 11 vis[0][i]=1; 12 vis[1][cur-i+8]=1; 13 vis[2][cur+i]=1; 14 search(cur+1); 15 //改回辅助的全局变量 16 vis[0][i]=0; 17 vis[1][cur-i+8]=0; 18 vis[2][cur+i]=0; 19 } 20 } 21 } 22 }
最终我们可以去得到答案：
1 int vis[3][15],tot; 2 int main() 3 { 4 search(0); 5 cout<<tot<<endl; 6 }
2.图的着色问题
给定无向连通图G=(V,E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。如果一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称m为该图的色数。地图着色问题可转换为图的着色问题：以地图中的区域作为图中顶点，2个区域如果邻接，则这2个区域对应的顶点间有一条边，即边表示了区域间的邻接关系。著名的四色定理就是指每个平面地图都可以只用四种颜色来染色，而且没有两个邻接的区域颜色相同。
给定图和颜色的数目求出着色方法的数目，可以使用回溯法。
参考函数如下：
1 bool ok(int k) 2 { 3 for(int j=1;j<=v;j++) 4 { 5 if(graph[k][j]&&(color[j]==color[k])) return false; 6 } 7 return true; 8 }
1 void backtrack(int t) 2 { 3 if(t>v) sum++; 4 else 5 { 6 for(int i=1;i<=c;i++) 7 { 8 color[t]=i; 9 if(ok(t)) backtrack(t+1); 10 //改回辅助的全局变量 11 color[t]=0; 12 } 13 } 14 }
最终我们可以去得到答案：
1 #define N 100 2 int v,e,c,graph[N][N],color[N]; 3 //顶点数,边数,颜色数 4 int sum; 5 int main() 6 { 7 int i,j; 8 cin>>v>>e>>c; 9 for(i=1;i<=v;i++) 10 { 11 for(j=1;j<=v;j++) 12 { 13 graph[i][j]=0; 14 } 15 } 16 for(int k=1;k<=e;k++) 17 { 18 cin>>i>>j; 19 graph[i][j]=1; 20 graph[j][i]=1; 21 } 22 for(i=0;i<=v;i++) color[i]=0; 23 backtrack(1); 24 cout<<sum<<endl; 25 }
3.装载问题
有一批共n个集装箱要装上2艘载重量分别为c1和c2的船，其中集装箱i的重量为wi，且
。装载问题要求确定是否有一个合理的装载方案可将这些集装箱装上这2艘船。如果有，找出一种装载方案。例如当n=3，c1=c2=50且w=[10,40,40]时，则可以将集装箱1和2装到第一艘轮船上，而将集装箱3装到第二艘轮船上；如果w=[20,40,40]，则无法将这3个集装箱都装上轮船。容易证明，如果一个给定装载问题有解，则首先将第一艘船尽可能装满再将剩余的集装箱装上第二艘船可得到最优装载方案。将第一艘船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近c1。用回溯法解装载问题, 时间复杂度O(2^n)，在某些情况下优于动态规划算法。剪枝方案是如果当前已经选择的全部物品载重量cw+剩余集装箱的重量r<=当前已知的最优载重量bestw，则删去该分支。
1 void backtrack(int i) 2 { 3 if(i>n) 4 { 5 if(ans>bestans) bestans=ans; 6 return; 7 } 8 r-=w[i]; 9 if(ans+w[i]<=c1) 10 { 11 ans+=w[i]; 12 backtrack(i+1); 13 //改回辅助的全局变量 14 ans-=w[i]; 15 } 16 if(ans+r>bestans) backtrack(i+1); 17 //改回辅助的全局变量 18 r+=w[i]; 19 }
1 int maxloading() 2 { 3 ans=0; 4 bestans=0; 5 backtrack(1); 6 return bestans; 7 }
最终我们可以去得到答案：
1 int n;//集装箱数 2 int w[40];//集装箱重量 3 int c1,c2;//两艘船的载重量 4 int ans;//当前载重量 5 int bestans;//当前最优载重量 6 int r;//剩余集装箱重量 7 int main() 8 { 9 cin>>n>>c1>>c2; 10 int i=1; 11 int sum=0; 12 //集装箱总重量 13 while(i<=n) 14 { 15 cin>>w[i]; 16 r+=w[i]; 17 sum+=w[i]; 18 i++; 19 } 20 maxloading(); 21 if(bestans>0&&((sum-bestans)<=c2)) cout<<bestans<<endl; 22 else if(sum<=c2) cout<<bestans<<endl; 23 else cout<<"No"<<endl; 24 }
4.批处理作业调度问题
给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需(1≤i≤n)要机器j(1≤j≤2)的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和：。要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。
| tji | 机器1 | 机器2 |
| 作业1 | 2 | 1 |
| 作业2 | 3 | 1 |
| 作业3 | 2 | 3 |
例如，对于这张表格所示的情况，3个作业有3!=6种可能调度方案，很显然最坏复杂度即为O(n!)。如果按照2,3,1的顺序,则作业2的完成时间为4，作业3的完成时间为8，作业1的完成时间为9，完成时间和为21。最优的作业调度顺序为最佳调度方案是1,3,2，其完成时间和为18。
1 void backtrack(int k) 2 { 3 if(k>number) 4 { 5 for(int i=1;i<=number;i++) bestorder[i]=xorder[i]; 6 bestvalue=xvalue; 7 } 8 else 9 { 10 for(int i=k;i<=number;i++) 11 { 12 f1+=x1[xorder[i]]; 13 f2[k]=(f2[k-1]>f1?f2[k-1]:f1)+x2[xorder[i]]; 14 xvalue+=f2[k]; 15 swap(xorder[i],xorder[k]); 16 if(xvalue<bestvalue) backtrack(k+1); 17 swap(xorder[i],xorder[k]); 18 xvalue-=f2[k]; 19 f1-=x1[xorder[i]]; 20 } 21 } 22 } 23
最终我们可以去得到答案：
1 #define MAX 200 2 int* x1;//作业Ji在机器1上的工作时间 3 int* x2;//作业Ji在机器2上的工作时间 4 int number=0;//作业的数目 5 int* xorder;//作业顺序 6 int* bestorder;//最优的作业顺序 7 int bestvalue=MAX;//最优的时间 8 int xvalue=0;//当前完成用的时间 9 int f1=0;//机器1完成的时间 10 int* f2;//机器2完成的时间 11 int main() 12 { 13 cout<<"请输入作业数目："; 14 cin>>number; 15 x1=new int[number+1]; 16 x2=new int[number+1]; 17 xorder=new int[number+1]; 18 bestorder=new int[number+1]; 19 f2=new int[number+1]; 20 x1[0]=0; 21 x2[0]=0; 22 xorder[0]=0; 23 bestorder[0]=0; 24 f2[0]=0; 25 cout<<"请输入每个作业在机器1上所用的时间："<<endl; 26 int i; 27 for(i=1;i<=number;i++) 28 { 29 cout<<"第"<<i<<"个作业="; 30 cin>>x1[i]; 31 } 32 cout<<"请输入每个作业在机器2上所用的时间："<<endl; 33 for(i=1;i<=number;i++) 34 { 35 cout<<"第"<<i<<"个作业="; 36 cin>>x2[i]; 37 } 38 for(i=1;i<=number;i++) xorder[i]=i; 39 backtrack(1); 40 cout<<"最节省的时间为："<<bestvalue<<endl; 41 cout<<"对应的方案为："; 42 for(i=1;i<=number;i++) cout<<bestorder[i]<<" "; 43 cout<<endl; 44 }
5.01背包问题
当然，回溯问题还可以用来解决01背包问题，对01背包不清楚的请移步至这里
下面贴下01背包的模板
1 void backtrack(int i,int cp,int cw) 2 { 3 if(i>n) 4 { 5 if(cp>bestp) 6 { 7 bestp=cp; 8 for(i=1;i<=n;i++) bestx[i]=x[i]; 9 } 10 } 11 else 12 { 13 for(int j=0;j<=1;j++) 14 { 15 x[i]=j; 16 if(cw+x[i]*w[i]<=c) 17 { 18 cw+=w[i]*x[i]; 19 cp+=p[i]*x[i]; 20 backtrack(i+1,cp,cw); 21 cw-=w[i]*x[i]; 22 cp-=p[i]*x[i]; 23 } 24 } 25 } 26 }
最终我们可以去得到答案：
1 int n,c,bestp;//物品个数,背包容量,最大价值 2 int p[10000],w[10000],x[10000],bestx[10000];//物品的价值,物品的重量,物品的选中情况 3 int main() 4 { 5 bestp=0; 6 cin>>c>>n; 7 for(int i=1;i<=n;i++) cin>>w[i]; 8 for(int i=1;i<=n;i++) cin>>p[i]; 9 backtrack(1,0,0); 10 cout<<bestp<<endl; 11 }
6.最大团问题
给定无向图G=(V, E)，U是V的子集。如果对任意u,v属于U有(u,v)属于E，则称U是G的完全子图。G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。如果对任意u,v属于U有(u, v)不属于E，则称U是G的空子图。G的空子图U是G的独立集当且仅当U不包含在G的更大的空子图中。G的最大独立集是G中所含顶点数最多的独立集。G的补图G\'=(V\',
E\')定义为V\'=V且(u, v)属于E\'当且仅当(u, v)不属于E。
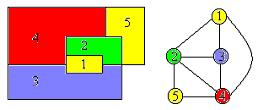
如图所示，给定无向图G={V, E}，其中V={1,2,3,4,5}，E={(1,2),(1,4),(1,5),(2,3),(2,5),(3,5),(4,5)}。根据最大团定义，子集{1,2}是图G的一个大小为2的完全子图，但不是一个团，因为它包含于G的更大的完全子图{1,2,5}之中。{1,2,5}是G的一个最大团。{1,4,5}和{2,3,5}也是G的最大团。右侧图是无向图G的补图G\'。根据最大独立集定义，{2,4}是G的一个空子图，同时也是G的一个最大独立集。虽然{1,2}也是G\'的空子图，但它不是G\'的独立集，因为它包含在G\'的空子图{1,2,5}中。{1,2,5}是G\'的最大独立集。{1,4,5}和{2,3,5}也是G\'的最大独立集。
最大团问题可以用回溯法在O(n2^n)的时间内解决。首先设最大团为一个空团，往其中加入一个顶点，然后依次考虑每个顶点，查看该顶点加入团之后仍然构成一个团。程序中采用了一个比较简单的剪枝策略，即如果剩余未考虑的顶点数加上团中顶点数不大于当前解的顶点数，可停止回溯。用邻接矩阵表示图G，n为G的顶点数，cn存储当前团的顶点数，bestn存储最大团的顶点数。当cn+n-i<bestn时，不能找到更大的团，利用剪枝函数剪去。
1 void backtrack(int i) 2 { 3 if(i>v) 4 { 5 if(cn>bestn) 6 { 7 bestn=cn; 8 for(int j=1;j<=v;j++) bestuse[j]=use[j]; 9 return; 10 } 11 } 12 bool flag=true; 13 for(int j=1;j<i;j++) 14 { 15 if(use[j]&&!graph[j][i]) 16 { 17 flag=false; 18 break; 19 } 20 } 21 if(flag) 22 { 23 cn++; 24 use[i]=true; 25 backtrack(i+1); 26 use[i]=false; 27 cn--; 28 } 29 if(cn+v-i>bestn) 30 { 31 use[i]=false; 32 backtrack(i+1); 33 } 34 }
最终我们可以去得到答案：
1 const int maxnum=101; 2 bool graph[maxnum][maxnum]; 3 bool use[maxnum],bestuse[maxnum]; 4 int cn,bestn,v,e; 5 int main() 6 { 7 cin>>v>>e; 8 for(int i=1;i<=e;i++) 9 { 10 int p1,p2; 11 cin>>p1>>p2; 12 graph[p1][p2]=true; 13 graph[p2][p1]=true; 14 } 15 backtrack(1); 16 cout<<bestn<<endl; 17 for(int i=1;i<=v;i++) 18 { 19 if(bestuse[i]) cout<<i<<" "; 20 } 21 cout<<endl; 22 }
7.圆排列问题
给定n个大小不等的圆c1,c2,…,cn，现要将这n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如，当n=3，且所给的3个圆的半径分别为1，1，2时，这3个圆的最小长度的圆排列如图所示。其最小长度为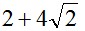
。
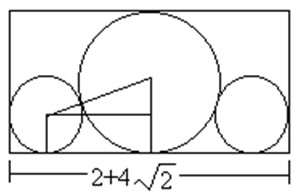
注意，下面代码中圆排列的圆心横坐标以第一个圆的圆心为原点。所以，总长度为第一个圆的半径+最后一个圆的半径+最后一个圆的横坐标。
1 //计算当前所选择圆的圆心横坐标 2 float center(int t) 3 { 4 float temp=0; 5 for(int j=1;j<t;j++) 6 { 7 //由x^2=sqrt((r1+r2)^2-(r1-r2)^2)推导而来 8 float valuex=x[j]+2.0*sqrt(r[t]*r[j]); 9 if(valuex>temp) temp=valuex; 10 } 11 return temp; 12 }
1 //计算当前圆排列的长度 2 void compute() 3 { 4 float low=0,high=0; 5以上是关于回溯算法入门及经典案例剖析(初学者必备宝典)的主要内容，如果未能解决你的问题，请参考以下文章