README回溯算法基本框架

Posted 2021-05-16 快乐江湖

前言

回溯算法是一个非常经典的算法，像图中的DFS（深度优先遍历）其核心思想就是回溯，但是初学者对于回溯总是感觉一头雾水，不知所措，但熟不知，回溯算法也是尤其“套路”的

原创声明

本人在学习回溯算法时也感觉比较困惑，但是有幸看到一本非常好的算法书籍，也算是解决了我很多疑惑，我发现有些东西不是我智商不够，而是缺乏训练，尤其是有目的，有逻辑的训练。
本文皆是我在阅读它的书后所做的一些整理，发表一下自己的看法。如果有兴趣的小伙伴可以移步

labuladong的算法小抄

题目

一：回溯算法的本质和框架（结合全排列）

（1）回溯算法的本质

回溯算法本质是一个暴力穷举的过程，你会发现涉及回溯算法的题目都有一个共同特点：列出所有满足的情况
而且做得多了，你也会有种感觉，就是每个能用回溯算法解决的题目总能画出一个二叉树来，比如LeetCode 46：全排列这就是一道打开回溯算法大门的经典题，而它对应的二叉树是这样的

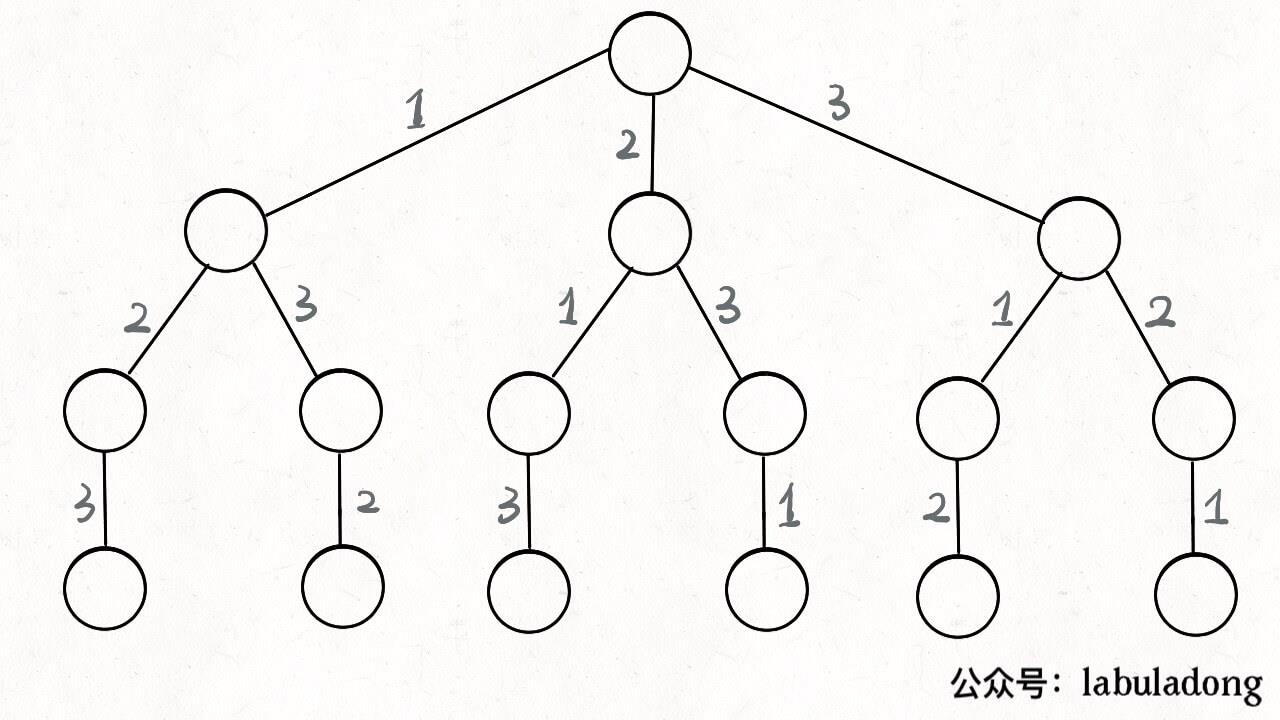
在回溯算法中，我们称这样的树为决策树，解决一个回溯问题，其实就是一个决策树的遍历过程

（2）回溯算法的框架

遍历整个决策树时，你只需要思考三个问题：

• 路径：你已经做出的选择
• 选择列表：也就是你当前可以做的选择
• 结束条件：到达决策树底层，无法再做选择的条件

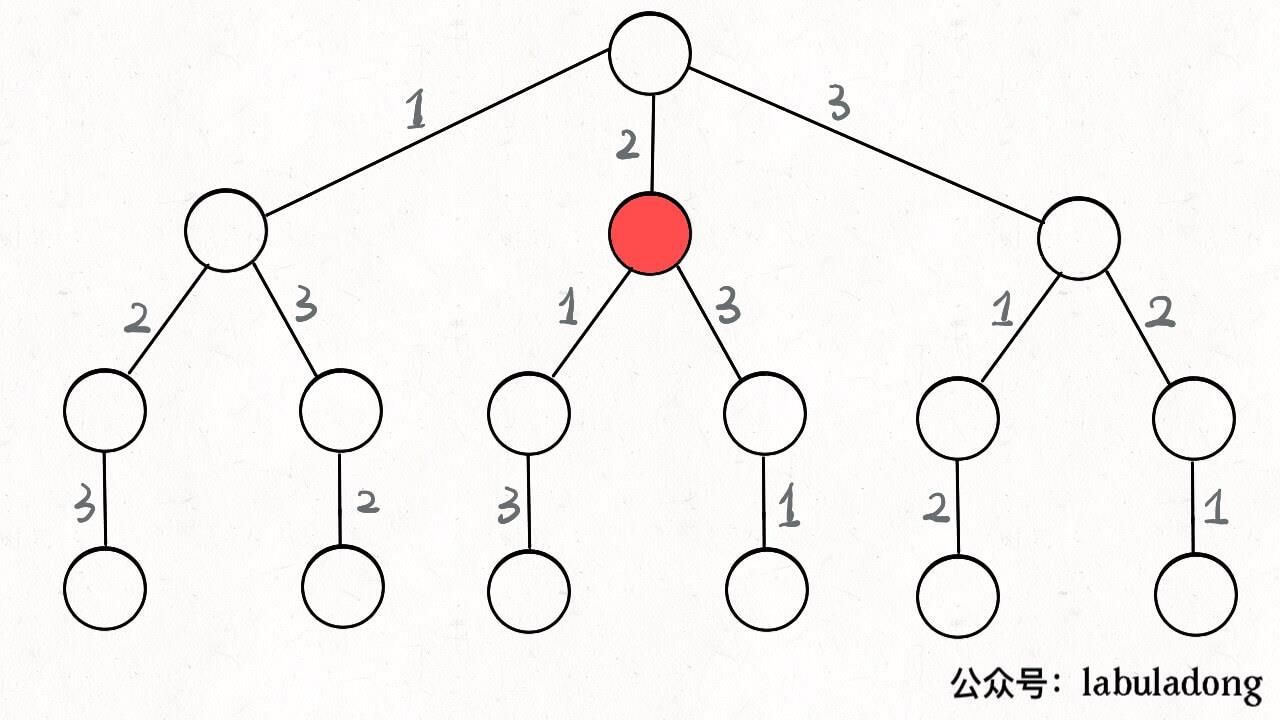
以全排列为例：说明上面的含义，全排列的决策树如下

完成全排列，这三个位置的数字是不能够重复的，所以假如你站到了根节点上，你就可以做出决策了，你现在可以选择1或2或3，为什么呢，因为刚开始你还没有做出选择；好的现在你做出了选择，选择了2，也就是到达了红色的结点，那么你现在的路径就是2，它记录了你已经做出的选择，现在你可以选择1或3，那么它就是你的选择列表；，然后当你走的树的最底层时你会发现你没得选择，于是你到达了结束条件，同时此时的选择列表为空

现在我们可以拿出回溯算法的框架了，解决回溯算法类的题目时，你只需要按照这种角度去思考，不能保证一定能解出来，但是至少能保证已经非常接近正确答案了。至少能保证，你看见某个题目，即使你想不出来，但是你知道应该怎么去靠近正确解法，因为能不能解出来，最重要的还是要靠你的理解能力。

下面result通常设为一个全局变量，用于返回结果，前面我们就说过，回溯算法本质就是在遍历决策树，所以那个backtrack其实就是在实现这样的需求，下面的for循环时在做出选择，然后再进行backtrack递归。需要注意的是做选择做出的是合理的选择，就拿全排列而言，做选择时一定要选择在选择列表中不属于路径的元素，通俗的讲就是你已经选择了2，然后再选择时候就不能选择2了，只能选择1或3了

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

上面的框架中，有一点我相信大家是肯定有疑惑的，那就是为什么要撤销选择
前面我们就说过，回溯算法本质就是在遍历决策树，那么新的问题又来了：如何遍历？如何遍历我就不用说了，我要特别强调的是它的本质，因为很多人老是按照“左中右”，“左右中”这种方式去记忆树的遍历，无法体会到其精髓。
就拿前序和后序来说，你能说出其本质是什么吗？本质就是它是进入某个结点之前就行执行操作还是离开某个结点之后再执行操作的问题

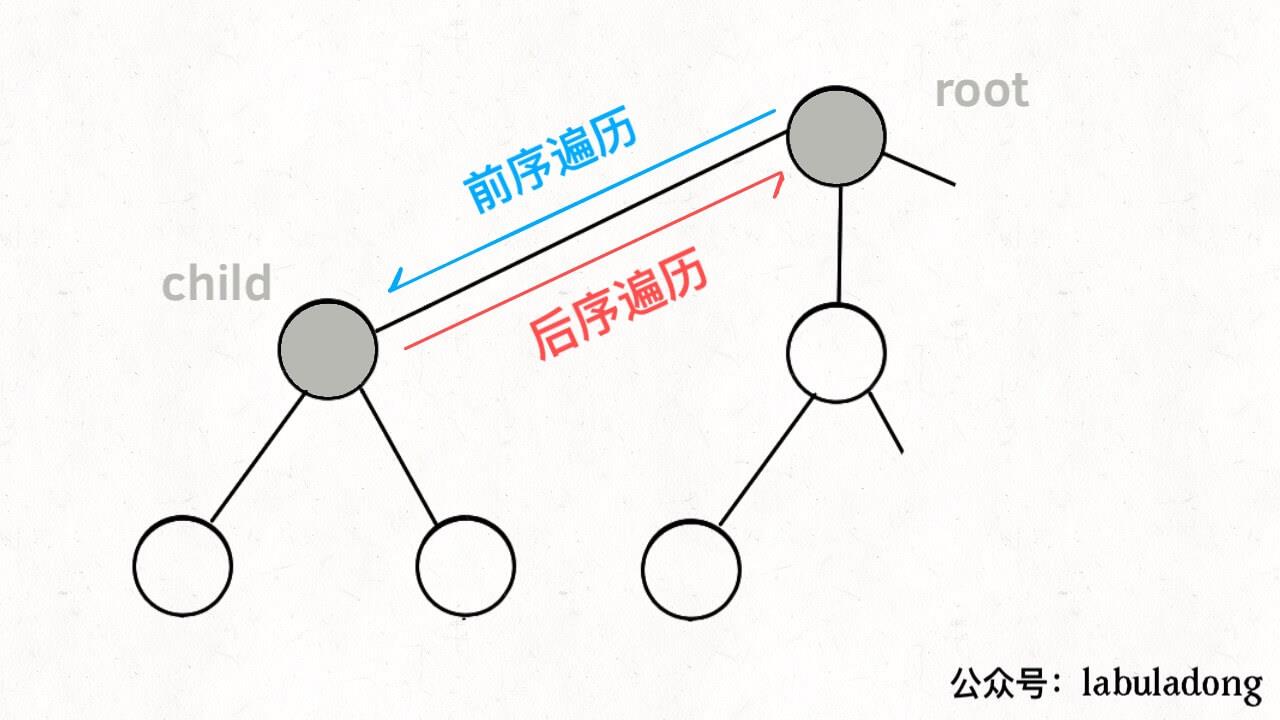
大家可以想一想，你的一次选择结束了，你肯定要返回当当时进入递归时的状态，然后进行另外的选择啊，不然你不返回状态，其他选择怎么办。如果不撤销，按照上图的角度，你只会得到一个结果，就是用于遍历的左子树。

好的至此，基本的问题就讲清楚了，我相信大家肯定还有诸多疑惑，但是没有关系，做完全排列你就会读回溯有了新的理解