洛谷T21776 子序列

Posted 2020-10-24 自为

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了洛谷T21776 子序列相关的知识，希望对你有一定的参考价值。

题目描述

你有一个长度为 nn 的数列 \\{a_n\\}{an​} ，这个数列由 0,10,1 组成，进行 mm 个的操作：

1~l~r1 l r ：把数列区间 [l, r][l,r] 内的所有数取反。即 00 变成 11 ，11 变成 00 。

2~l~r2 l r ：询问数列在区间 [l, r][l,r] 内共有多少个本质不同的子序列。

输入输出格式

输入格式：

 

第一行包含两个整数 n, mn,m ，意义如上所述。

接下来一行包含 nn 个数，表示数列 \\{a_n\\}{an​} 。

接下来 mm 行，每行包含三个数，表示一个操作，操作格式如上所述。

 

输出格式：

 

对于每个询问，输出答案模 10^9 + 7109+7 的结果。

 

输入输出样例

输入样例#1： 复制

4 4
1 0 1 0
2 1 4
2 2 4
1 2 3
2 1 4

输出样例#1： 复制

11
6
8

说明

对于 10 \\%10% 的数据，1 \\leq n, m \\leq 10^21≤n,m≤102 。

对于 30 \\%30% 的数据，1 \\leq n, m \\leq 10^31≤n,m≤103 。

对于 100 \\%100% 的数据，1 \\leq n, m \\leq 10^51≤n,m≤105 。

 

这道题同HDU6155（只不过我在HDU上T飞了）

首先我们考虑一下暴力怎么写

dp[i][1]表示到第$i$个位置，以$1$结尾，本质不同的子序列

dp[i][0]表示到第$i$个位置，以$0$结尾，本质不同的子序列

转移的时候，假设第$i$个字符是1

那么对它有贡献的是以前以$0$结尾的子序列，以及以前以$1$结尾的子序列，以及空串

那么此时

$dp[i][1]=dp[i-1][0]+dp[i-1][1]+1$

$dp[i][0]=dp[i-1][0]$

当第$i$个字符是$0$的时候同理，不难得到

$dp[i][1]=dp[i-1][1]$

$dp[i][0]=dp[i-1][0]+dp[i-1][1]+1$

大家有没有发现一件事情?

这个dp的转移是递推！也就是说我们可以用矩阵乘法来加速！

而矩阵乘法可以用线段树来维护！

它的矩阵为

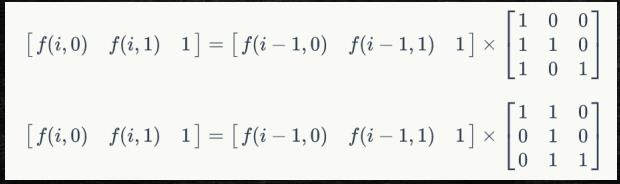
对于操作1的话，先交换要改变的矩阵的第一行和第二行，再交换要改变的矩阵的第一列和第二列

至于为什么？这个可以转移之间的关系入手，也可以直接找规律

这样就实现了两个矩阵的转换

另外还有一点、

对于结果矩阵，我们只会用到[3][1]和[3][2]这两项（分别代表dp[n][1],dp[n][0]）

// luogu-judger-enable-o2
// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cstring>
#define LL long long int 
#define ls k<<1
#define rs k<<1|1
using namespace std;
const int MAXN=1e6+10;
const int mod=1e9+7;
inline int read()
{
    char c=getchar();int x=0,f=1;
    while(c<\'0\'||c>\'9\'){if(c==\'-\')f=-1;c=getchar();}
    while(c>=\'0\'&&c<=\'9\'){x=x*10+c-\'0\';c=getchar();}
    return x*f;
}
char c[MAXN];
struct Matrix
{
    LL mat[4][4];
    Matrix(){memset(mat,0,sizeof(mat));}
};
struct node
{
    int l,r,w;
    bool f;
    Matrix m;    
}T[MAXN];
Matrix zero,one,HHHHH;
Matrix rev(Matrix &a)
{
    for(LL i=1;i<=3;i++) swap(a.mat[1][i],a.mat[2][i]);
    for(LL i=1;i<=3;i++) swap(a.mat[i][1],a.mat[i][2]);
}
Matrix MatrixMul(Matrix a,Matrix b)
{
    Matrix c;
    for(LL k=1;k<=3;k++)
        for(LL i=1;i<=3;i++)
            for(LL j=1;j<=3;j++)
                c.mat[i][j]=(c.mat[i][j]+(a.mat[i][k]*b.mat[k][j])%mod )%mod;
    return c;
}
void update(int k)
{
    T[k].m=MatrixMul(T[ls].m,T[rs].m);
}
void pushdown(int k)
{
    if(T[k].f)
    {
        T[ls].f^=1;T[rs].f^=1;
        rev(T[ls].m);rev(T[rs].m);
        T[k].f=0;
    }
}
void Build(int k,int ll,int rr)
{
    T[k].l=ll;T[k].r=rr;T[k].f=0;
    if(ll==rr)
    {
        if(c[ll]==\'0\') T[k].m=zero;
        else T[k].m=one;
        return ;
    }
    int mid=ll+rr>>1;
    Build(ls,ll,mid);
    Build(rs,mid+1,rr);
    update(k);
}
void IntervalChange(int k,int ll,int rr)
{
    if(ll<=T[k].l&&T[k].r<=rr)
    {
        T[k].f^=1;
        rev(T[k].m);
        return ;
    }
    pushdown(k);
    int mid=T[k].l+T[k].r>>1;
    if(ll<=mid) IntervalChange(ls,ll,rr);
    if(rr>mid)  IntervalChange(rs,ll,rr);
    update(k);
}
Matrix IntervalAsk(int k,int ll,int rr)
{
    Matrix ans=HHHHH;
    if(ll<=T[k].l&&T[k].r<=rr)
    {
        ans=T[k].m;
        return ans;
    }
    pushdown(k);
    LL mid=T[k].l+T[k].r>>1;
    if(ll<=mid) 
        ans=MatrixMul(IntervalAsk(ls,ll,rr),ans);
    if(rr>mid)  
        ans=MatrixMul(ans,IntervalAsk(rs,ll,rr));
    return ans;
}
int main()
{
    int N,M;
    zero.mat[1][1]=zero.mat[2][1]=zero.mat[3][1]=zero.mat[2][2]=zero.mat[3][3]=1;
    one.mat[1][1]=one.mat[1][2]=one.mat[2][2]=one.mat[3][2]=one.mat[3][3]=1;
    HHHHH.mat[1][1]=HHHHH.mat[2][2]=HHHHH.mat[3][3]=1;
    int T;
    T=1;
    while(T--)
    {
        N=read();M=read();
        scanf("%s",c+1);
        Build(1,1,N);
        while(M--)
        {
            int opt=read(),l=read(),r=read();
            if(opt==1)
            {
                IntervalChange(1,l,r);
            }
            else if(opt==2)
            {
                Matrix ans=IntervalAsk(1,l,r);
                printf("%lld\\n", (ans.mat[3][1]+ans.mat[3][2])%mod );
            }
        }        
    }
    return 0;
}