近在学习《机器学习实战》这本书，做了一些笔记，和大家分享下：
一 、K-近邻算法（KNN）概述
最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。
KNN是通过测量不同特征值之间的距离进行分类。它的的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
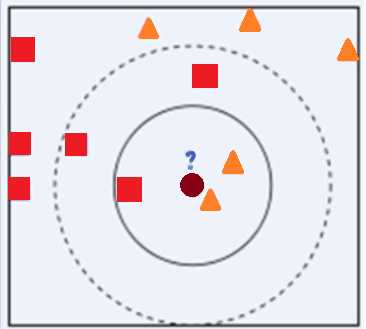
下面通过一个简单的例子说明一下：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。
二、算法伪代码：
搜索k个近邻的算法：kNN(A[n],k)
输入：A[n]为N个训练样本在空间中的坐标，k为近邻数
输出：x所属的类别
取A[1]~A[k]作为x的初始近邻，计算与测试样本x间的欧式距离d（x,A[i]）,i=1,2,.....,k；按d（x，A[i]）升序排序，计算最远样本与x间的距离D<-----max{d(x,a[j]) | j=1,2,.....,k};
for(i=k+1;i<=n;i++)
计算a[i]与x间的距离d(x,A[i]);
if(d(x,A[i]))<D
then 用A[i]代替最远样本
按照d(x,A[i])升序排序，计算最远样本与x间的距离D<---max{d(x,A[j]) | j=1,...,i };计算前k个样本A[i]),i=1,2,...,k所属类别的概率，具有最大概率的类别即为样本x的类
三、算法小结
k-近邻算法是分类数据最简单最有效的算法，它基于实例的学习，使用算法时必须有接近实际数据（能够反映实际数据）的训练样本集。使用K-近邻算法必须保存所有训练数据，如果数据很大，占用空间很大。而且，对一个样本分类，必须计算其与所有训练样本集中的样本的距离，这可能会非常耗时。k-近邻的改进算法为k决策树。