机器学习之k-近邻算法实践学习

Posted 2020-10-18 蓝色之旅

       关于本文说明，本人原博客地址位于http://blog.csdn.net/qq_37608890，本文来自笔者于2017年12月04日 22:54:26所撰写内容（http://blog.csdn.net/qq_37608890/article/details/78714664）。

   

    本文根据最*学*机器学*书籍 网络文章的情况,特将一些学*思路做了归纳整理,详情如下.如有不当之处,请各位大拿多多指点,在此谢过.

一、k-*邻算法(k-Nearest Neighbor，KNN)概述

1、简言之，k-*邻算法采用测量不同特征值之间的距离方法进行分类。

2、工作原理

     存在一个样本数据集合，也称为训练样本集，且样本集中每个数据都存在标签，也就是众所周知样本集中每一数据与所属分类的对应关系。输入没有标签的新数据以后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最*邻）的分类标签。一般情况下，我们只选择样本数据集中前k个最相似的数据，这就是k-*邻算法中k的出处，通常k是不大于20的整数。最终，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

3、k-*邻算法的一般流程

     （1） 收集数据：可以使用任何方法。
     （2） 准备数据： 距离计算所需要的数值，最好是结构化数据格式。
     （3） 分析数据： 可以使用任何方法。
     （4） 训练算法： 此步骤不适用K-*邻算法。
     （5） 测试算法： 计算错误率。
      （6） 使用算法： 首先需要输入样本数据和结构化的输出结果，然后运行k-*邻算法判定输入数据分别属于哪个分类，最后应用对计算出的分类执行后续的处理。

4、相关特性

    （1）优点： 精度高，对异常值不敏感、无输入假定。

     （2）缺点： 计算复杂度高、空间复杂度高。

     （3）适用数据范围： 数值型和标称型。

   kNN是non-parametric分类器（不做分布形式的假设，直接从数据估计概率密度），是memory-based learning，不适用于高维数据（curse of dimension)，算法复杂度高（可用KD树优化）。另外，k越小越容易过拟合，但是k很大会将分类精度（设想极限情况：k=1和k=N（样本数））。

    

二、k-*邻场景

     我们知道，电影可以按题材分类，但题材本身是如何定义的？由谁来判定某部电影属于哪个题材？即同一题材的电影会具有哪些公共特征？这些都是在做电影分类时一定要搞清楚的问题。这里以动作片和爱情片为例做简要说明。动作片具有哪些公共特征，使得动作片之间非常相似，却明显有别于爱情片？动作片中也可能有接吻镜头，爱情片中也可能存在打斗镜头，所以，不能简单地依靠是否存在打斗或者接吻来判断一部电影的类型。但很明显的是，动作片中的打斗镜头更多、爱情片中的接吻次数更频繁，基于此类场景在一部电影中出现的次数可用来进行电影分类。

   有人曾经统计过很多电影的打斗镜头和接吻镜头， 下方图1-1 给出了6部电影的打斗和接吻镜头。假如现在有一部从未看过的电影，你如何判断它属于动作片还是爱情片呢？

 

 

 

                 图1-1

 

     首先，我们弄清楚这部未知电影中存在多少打斗镜头、多少接吻镜头，图1-1中问号位置是该未知电影出现的镜头数图示，具体见下方表1-1。

 

表1-1每部电影的打斗镜头数、接吻镜头数及电影评估类型

    由图1-1和表1-1，可用将未知电影在图1-1的具体位置标出，利用欧式距离公式，计算出未知电影与样本集中其他电影之间的距离，相见下方表2-2所示。

表2-2 已知电影与未知电影之间的距离

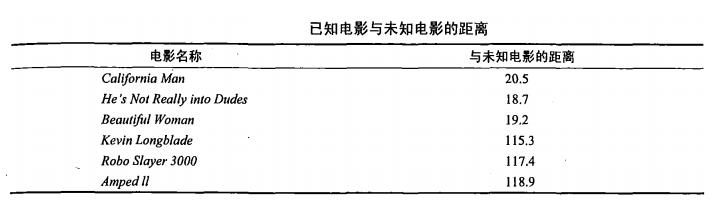
        由表2-2所示，显然，如果样本集中所有电影与未知电影之间的距离按照递增排序的话，可以得到k个距离最*的电影，这里假设k=2的话，则未知电影与电影He’s Not Really into Dudes，Beautiful Woman影片类型最为相似，判定未知电影属于爱情片。

 

三、示例：使用kNN算法优化约会网站的配对效果

    特别提醒：有些教材或博客，在代码实现过程中，由于python2.x和python3.x的不同，在实际执行过程中出现语法错误，这里特做提醒，print语句将输出内容一律加上();另外，python3.0版本后用input替换了raw_input，请读者注意。

1、项目概述

       海伦在使用约会网站寻找自己的约会对象。总结经验之后，她发现曾交往过的人分三种类型:

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

     她期待：

• 工作日与魅力一般的人约会
• 周末与极具魅力的人约会
• 不喜欢的人则直接排除掉

2、  k-*邻算法开发实现流程

• 收集数据：提供文本文件

•  准备数据：使用 Python 解析文本文件

•  分析数据：使用 Matplotlib 画二维散点图

•  训练算法：此步骤不适用于 k-*邻算法

•  测试算法：使用海伦提供的部分数据作为测试样本。         测试样本和非测试样本的区别在于：             测试样本是已经完成分类的数据，如果预测分类与实际类别不同，则标记为一个错误。

•  使用算法：产生简单的命令行程序，然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型。 

3、   准备数据:从文本文件中解析数据

         目前,海伦搜集来一些约会对象的数据,并把这些数据存放在文本文件 datingTestSet2.txt 中，每个样本数据占据一行,总共有 1000 行。这些样本数据主要包含以下 3 种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所耗时间百分比
• 每周消费的冰淇淋公升数

而文本文件datingTestSet2.txt的数据格式如下：


40999    9.161978      1.110180      3
15823    0.991725      0.730979      2
35432    7.398380      0.684218      3
53711    12.149747     1.389088      3
64371    9.149678      0.874905      1
9289    9.666576       1.370330      2

 

准备数据：使用 Python 解析文本文件

将文本记录转换为 NumPy 的解析程序

    def file2matrix(filename):  
       """ 
       Desc: 
           导入训练数据 
       parameters: 
           filename: 数据文件路径 
       return:  
           数据矩阵 returnMat 和对应的类别 classLabelVector 
       """  
       fr = open(filename)  
       
       numberOfLines = len(fr.readlines())  
     
      
       returnMat = zeros((numberOfLines, 3))  # prepare matrix to return  
       classLabelVector = []  # prepare labels return  
       fr = open(filename)  
       index = 0  
       for line in fr.readlines():  
           
           line = line.strip()  
        
           listFromLine = line.split(\'\\t\')  
    
           returnMat[index, :] = listFromLine[0:3]  
     
           classLabelVector.append(int(listFromLine[-1]))  
           index += 1  
   
       return returnMat, classLabelVector  

 

执行如下命令
 

    datingDataMat,datingLabels=file2matrix(\'datingTestSet2.txt\')  
    datingDataMat  

 

得到

array([[  4.09200000e+04,   8.32697600e+00,   9.53952000e-01],
       [  1.44880000e+04,   7.15346900e+00,   1.67390400e+00],
       [  2.60520000e+04,   1.44187100e+00,   8.05124000e-01],
       ..., 
       [  6.88460000e+04,   9.97471500e+00,   6.69787000e-01],
       [  2.65750000e+04,   1.06501020e+01,   8.66627000e-01],
       [  4.81110000e+04,   9.13452800e+00,   7.28045000e-01]])

 

执行 datingLabels[0:20],得到

[3, 2, 1, 1, 1, 1, 3, 3, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 2, 3]

 

4、       分析数据：使用 Matplotlib 画二维散点图

 

执行如下代码  

    import matplotlib  
    import matplotlib.pyplot as plt  
    fig = plt.figure()  
    ax = fig.add_subplot(111)  
    ax.scatter(datingDataMat[:, 1], datingDataMat[:, 2], 15.0*array(datingLabels), 15.0*array(datingLabels))  
    plt.show()  

 

  得到如下图

 

 

 

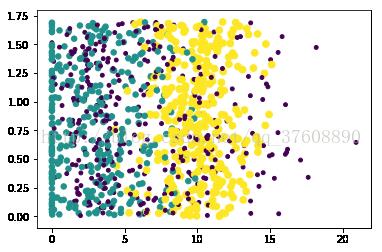
而下图中采用矩阵的第一和第三列属性得到很好的展示效果，清晰地标识了三个不同的样本分类区域，具有不同爱好的人其类别区域也不同。

5、     准备数据:归一化数值

       归一化数据 （归一化是一个让权重变为统一的过程)

序号	玩视频游戏所耗时间百分比	每年获得的飞行常客里程数	每周消费的冰淇淋公升数	样本分类
1	0.8	400	0.5	1
2	12	134 000	0.9	3
3	0	20 000	1.1	2
4	67	32 000	0.1	2

样本3和样本4的距离：

(0−67)2+(20000−32000)2+(1.1−0.1)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√

归一化特征值，消除特征之间量级不同导致的影响

归一化定义： 我是这样认为的，归一化就是要把你需要处理的数据经过处理后（通过某种算法）限制在你需要的一定范围内。首先归一化是为了后面数据处理的方便，其次是保正程序运行时收敛加快。 方法有如下：

• 线性函数转换，表达式如下：　　

  y=(x-MinValue)/(MaxValue-MinValue)　　

  说明：x、y分别为转换前、后的值，MaxValue、MinValue分别为样本的最大值和最小值。　　

• 对数函数转换，表达式如下：　　

  y=log10(x)　　

  说明：以10为底的对数函数转换。

  如图：

• 反余切函数转换，表达式如下：

  y=atan(x)*2/PI　

  如图：

• 式(1)将输入值换算为[-1,1]区间的值，在输出层用式(2)换算回初始值，其中和分别表示训练样本集中负荷的最大值和最小值。　　

在统计学中，归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布，归一化在-1--+1之间是统计的坐标分布。

    def autoNorm(dataSet):  
        """ 
        Desc: 
            归一化特征值，消除特征之间量级不同导致的影响 
        parameter: 
            dataSet: 数据集 
        return: 
            归一化后的数据集 normDataSet. ranges和minVals即最小值与范围，并没有用到 
     
        归一化公式： 
            Y = (X-Xmin)/(Xmax-Xmin) 
            其中的 min 和 max 分别是数据集中的最小特征值和最大特征值。该函数可以自动将数字特征值转化为0到1的区间。 
        """  
      
        minVals = dataSet.min(0)  
        maxVals = dataSet.max(0)  
     
        ranges = maxVals - minVals  
        normDataSet = zeros(shape(dataSet))  
        m = dataSet.shape[0]  
       
        normDataSet = dataSet - tile(minVals, (m, 1))  
     
        normDataSet = normDataSet / tile(ranges, (m, 1))  # element wise divide  
        return normDataSet, ranges, minVals  

 

训练算法：此步骤不适用于 k-*邻算法

     因为测试数据每一次都要与全量的训练数据进行比较，所以这个过程是没有必要的。

 

6 、   测试算法

           作为完整程序验证分类器

           使用海伦提供的部分数据作为测试样本。如果预测分类与实际类别不同，则标记为一个错误。

    kNN 分类器针对约会网站的测试代码

    def datingClassTest():  
        """ 
        Desc: 
            对约会网站的测试方法 
        parameters: 
            none 
        return: 
            错误数 
        """  
      
        hoRatio = 0.1  # 测试范围,一部分测试一部分作为样本  
     
        datingDataMat, datingLabels = file2matrix(\'datingTestSet2.txt\')  # load data setfrom file  
    
        normMat, ranges, minVals = autoNorm(datingDataMat)  

        m = normMat.shape[0]  
         
        numTestVecs = int(m * hoRatio)  
        print \'numTestVecs=\', numTestVecs  
        errorCount = 0.0  
        for i in range(numTestVecs):  
           
            classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)  
            print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))  
            if (classifierResult != datingLabels[i]): errorCount += 1.0  
        print ("the total error rate is: %f" % (errorCount / float(numTestVecs)))  
        print (errorCount)  

 

7、   使用算法:构建完整可用的系统

       上面已经在数据上对分类器进行了测试,现在则可以使用这个分类器帮助海伦对于约会对象进行分类,即海伦在网站上找到某人并输入他的信息,该程序会给出她对对方喜欢程度的预测值.

    def clasdifyPerson():  
        resultList = [\'not at all\', \'in small doses\', \'in large doses\']  
        percentTats = float(raw_input("percentage of time spent playing video games ?"))  
        ffMiles = float(raw_input("frequent filer miles earned per year?"))  
        iceCream = float(raw_input("liters of ice cream consumed per year?"))  
        datingDataMat, datingLabels = file2matrix(\'datingTestSet2.txt\')  
        normMat, ranges, minVals = autoNorm(datingDataMat)  
        inArr = array([ffMils, percentTats, iceCream])  
        classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels, 3)  
        print ("You will probably like this person: ", resultList[classifierResult - 1])  

 

实际运行效果如下:

>>> kNN.classifyPerson()
percentage of time spent playing video games?10
frequent flier miles earned per year?10000
liters of ice cream consumed per year?0.5
You will probably like this person: in small doses

 

四、   项目案例2: 手写数字识别系统

1、   项目概述

构造一个能识别数字 0 到 9 的基于 KNN 分类器的手写数字识别系统。

需要识别的数字是存储在文本文件中的具有相同的色彩和大小：宽高是 32 像素 * 32 像素的黑白图像。

2、   开发流程

收集数据：提供文本文件。 准备数据：编写函数 img2vector(), 将图像格式转换为分类器使用的向量格式 分析数据：在 Python 命令提示符中检查数据，确保它符合要求 训练算法：此步骤不适用于 KNN 测试算法：编写函数使用提供的部分数据集作为测试样本，测试样本与非测试样本的          区别在于测试样本是已经完成分类的数据，如果预测分类与实际类别不同，          则标记为一个错误 使用算法：本例没有完成此步骤，若你感兴趣可以构建完整的应用程序，从图像中提取          数字，并完成数字识别，美国的邮件分拣系统就是一个实际运行的类似系统 

收集数据: 提供文本文件

目录  trainingDigits中包含了大约 2000 个例子，每个例子内容如下图所示，每个数字大约有 200 个样本；目录 testDigits中包含了大约 900 个测试数据。

准备数据: 编写函数 img2vector(), 将图像文本数据转换为分类器使用的向量

将图像文本数据转换为向量

    def img2vector(filename):  
        returnVect = zeros((1,1024))  
        fr = open(filename)  
        for i in range(32):  
            lineStr = fr.readLine()  
            for j in range(32):  
                returnVect[0,32*i+j] = int(lineStr[j])  
        return returnVect  

 

分析数据：在 Python 命令提示符中检查数据，确保它符合要求

在 Python 命令行中输入下列命令测试 img2vector 函数，然后与文本编辑器打开的文件进行比较:

>>> testVector = kNN.img2vector(\'testDigits/0_13.txt\')
>>> testVector[0,0:31]
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
>>> testVector[0,31:63]
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

 

训练算法：此步骤不适用于 KNN

因为测试数据每一次都要与全量的训练数据进行比较，所以这个过程是没有必要的。

测试算法：编写函数使用提供的部分数据集作为测试样本，如果预测分类与实际类别不同，则标记为一个错误

def handwritingClassTest():  
   
    hwLabels = []  
    trainingFileList = listdir(\'trainingDigits\')  # load the training set  
    m = len(trainingFileList)  
    trainingMat = zeros((m, 1024))  

    for i in range(m):  
        fileNameStr = trainingFileList[i]  
        fileStr = fileNameStr.split(\'.\')[0]  # take off .txt  
        classNumStr = int(fileStr.split(\'_\')[0])  
        hwLabels.append(classNumStr)  
        # 将 32*32的矩阵->1*1024的矩阵  
        trainingMat[i, :] = img2vector(\'trainingDigits/%s\' % fileNameStr)  
  

    testFileList = listdir(\'testDigits\')  # iterate through the test set  
    errorCount = 0.0  
    mTest = len(testFileList)  
    for i in range(mTest):  
        fileNameStr = testFileList[i]  
        fileStr = fileNameStr.split(\'.\')[0]  # take off .txt  
        classNumStr = int(fileStr.split(\'_\')[0])  
        vectorUnderTest = img2vector(\'testDigits/%s\' % fileNameStr)  
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)  
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)  
        if (classifierResult != classNumStr): errorCount += 1.0  
    print ("\\nthe total number of errors is: %d" % errorCount)  
    print ("\\nthe total error rate is: %f" % (errorCount / float(mTest))) 

使用算法：本例没有完成此步骤，若你感兴趣可以构建完整的应用程序，从图像中提取数字，并完成数字识别，美国的邮件分拣系统就是一个实际运行的类似系统

五、   K-*邻算法小结

    截至目前,我们做一总结,k-*邻算法必须保存全部数据集,如果训练数据集很大,必须使用大量的存储空间.由于必须对数据集中的每个数据计算距离值,实际使用时可能非常耗时.此外,k-*邻还有以缺陷是它没办法给出任何数据的基础结构信息,也就无法得知平均实例样本和典型实例样本有哪些特征.而要解决这个问题,需要使用概率测量方法来处理.

k *邻算法有 三个基本的要素：

• k 值的选择

  • k 值的选择会对 k *邻算法的结果产生重大的影响。
  • 如果选择较小的 k 值，就相当于用较小的邻域中的训练实例进行预测，“学*”的*似误差（approximation error）会减小，只有与输入实例较*的（相似的）训练实例才会对预测结果起作用。但缺点是“学*”的估计误差（estimation error）会增大，预测结果会对*邻的实例点非常敏感。如果邻*的实例点恰巧是噪声，预测就会出错。换句话说，k 值的减小就意味着整体模型变得复杂，容易发生过拟合。
  • 如果选择较大的 k 值，就相当于用较大的邻域中的训练实例进行预测。其优点是可以减少学*的估计误差。但缺点是学*的*似误差会增大。这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误。 k 值的增大就意味着整体的模型变得简单。
  • *似误差和估计误差，请看这里：https://www.zhihu.com/question/60793482

• 距离度量

  • 特征空间中两个实例点的距离是两个实例点相似程度的反映。
  • k *邻模型的特征空间一般是 n 维实数向量空间 。使用的距离是欧氏距离，但也可以是其他距离，如更一般的 距离，或者 Minkowski 距离。

• 分类决策规则

  • k *邻算法中的分类决策规则往往是多数表决，即由输入实例的 k 个邻*的训练实例中的多数类决定输入实例的类。