机器学习基石笔记5——为什么机器可以学习
Posted tmortred
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习基石笔记5——为什么机器可以学习 相关的知识,希望对你有一定的参考价值。
Lecture 5. Training versus Testing
5.1 Recap and Preview
第四章介绍在假设空间有限的情况下, PAC 保证 Ein 和 Eout 足够的接近。 但是没有告诉我们如何让 Ein 足够的小。

图 5-1
如果 M 很小, PAC 保证 Ein 和 Eout 足够的接近。 但是 M 很小,不能保证存在一个 Ein 足够小的 h。
如果 M 很大,有可能存在 Ein 很小的 h。 但是 PAC 下, Eout 不一定是很小。显然M趋于无穷大时,表现非常不好,如何解决这个问题呢?
$$ \\mathbb{P}[| E_{in}(g) - E_{out}(g)| > \\epsilon ]\\leqslant 2M exp(-2\\epsilon^2N) $$ 公式 5-1
在第四节,我们得出公式 5-1。 现在看下是否能够找到一个较小的 m 来替代 M (很大或无穷)
$$ \\mathbb{P} [| E_{in}(g) - E_{out}(g) | > \\epsilon]\\leqslant 2m_\\mathcal{H} exp(-2\\epsilon^2N)$$ 公式 5-2
5.2 Effective Number of Lines

图 5-2
如图 5-2 所示, M 是 union bound ,也是上界但不是上确界。

图 5-3
如果有 2 个很接近的 hypothesis h1, h2 。 如图 5-3 所示 h1, h2 的 BAD DATA 集也基本上重合。 union bound over-estimating 上界。为了解决 overlap 问题,我们能不能尝试将相似的 hypothesis 分类?我们先举个例子,用一个点来看二元线性分类问题。如图 5-4 所示,一个点能把 hypothesis 从效果上分为2 类
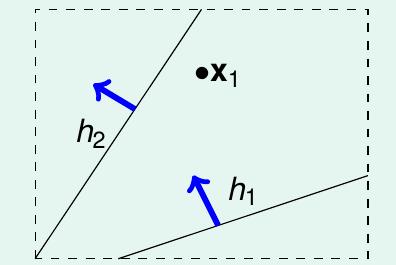
图 5-4
如图 5-5 所示, 2 个样本点可从效果上将 hypothesis 分为 4 类
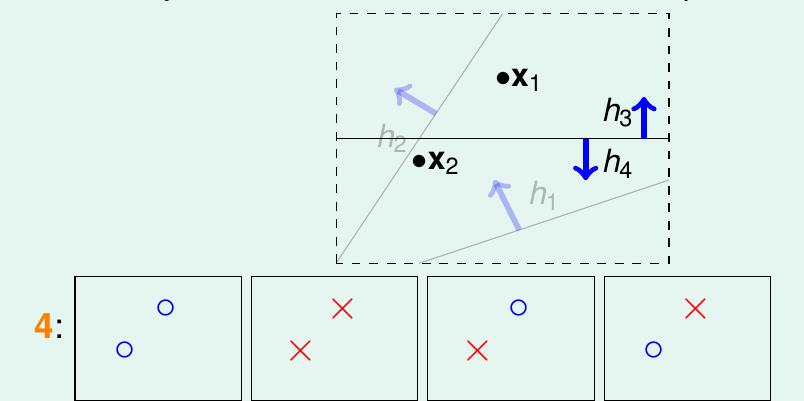
图 5-5
继续观察 3 个样本点的情况, 可以看出最多有个 8 种情况。
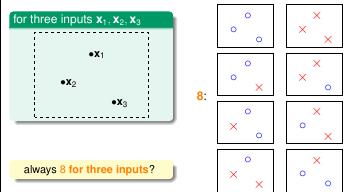
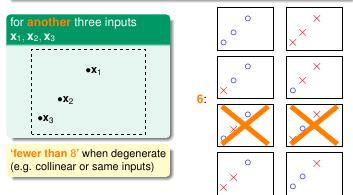
图 5-6 图 5-7
继续观察 4 个样本点的情况, 可以看出最多只有 14 种情况

图 5-8
我们可以看出 hypothesis 种类最多是 2N 。
5.3 Effective Number of Hypothesis
我们准备来用样本点来 group hypothesis, 但是存在一个问题。就好像 5.2 节所谈到的,3 个样本点既能把 hypothesis 分类 8 种,也能把 hypothesis 分类位为 6 种。碰到这种问题我们该怎么办? 为了方便后续的证明,我们取所有情况下最大的值。将样本点数 group H (x1, x2, ... xN ) 的最大值定义为 groupth function。
我们先看 3 个简单的 hypothesis 的 groupth function

图 5-9
从图 5-9 中可以看出, effective(H) 要远小于 2N (除了 convex sets)
$$ \\mathbb{P} [| E_{in}(g) - E_{out}(g) | > \\epsilon]\\leqslant 2 effective(\\mathcal{H}) exp(-2\\epsilon^2N)$$
5.4 Break Point

图 5-10
对平面上的二元分类或者其它问题。if no K inputs can be shattered by H, call K a beakpoint of H. also K+1, K+2 ... breakpoints too. 我们将 breakpoint 称之为一线曙光, 因为这意味 effectvie hypothesis is represented by a polynomial !
题外话:
1. 第 5 节课程名为 Training and Testing, 但是没看到 Training 和 Testing 相关的~~
2. 5.2 节许多知识,没有写到本笔记中来了。那些内容不是很复杂,很容易看出来不需要写进来备忘。其它同学还是看杜少的笔记,不要被我误导了
3. 5.3 将例子相关的全部跳过
以上是关于机器学习基石笔记5——为什么机器可以学习 的主要内容,如果未能解决你的问题,请参考以下文章