机器学习基石笔记6——为什么机器可以学习
Posted tmortred
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习基石笔记6——为什么机器可以学习相关的知识,希望对你有一定的参考价值。
Lecture 6: Theory of Generalization
6.1 Restriction of Break Point
$$ \\mathbb{P}[| E_{in}(g) - E_{out}(g)| > \\epsilon ]\\leqslant 2M exp(-2\\epsilon^2N) $$ 公式 6-1
$$ \\mathbb{P} [| E_{in}(g) - E_{out}(g) | > \\epsilon]\\leqslant 2m_\\mathcal{H} exp(-2\\epsilon^2N)$$ 公式 6-2
在学习第 4 节课时,我们知道对于 finite hypothesis, 即 M 有限。只要学习样本 N 足够大,就能保证 Ein 和 Eout PAC 近似相等。在学习第 5 节课时根据样本 inputs 的分类效果将 inifinite hypothesis 中 similar hypothesis group 起来。
对于 infinite hypothesis , 公式 6-1 中 M(一个无穷大的数) 可以替换为一个有限的 mH。用有限的 mH 来替换无限 M, 算是解决一个问题。同时也引入了一个新问题即 mH 也有点大, 粗略的分析对于任意的 K inputs 有 mH ≤ 2K 。 图 6-1 展示了指数增长的速度
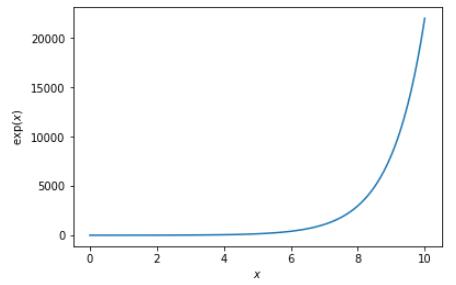
图 6-1 指数函数
用 2N 来代换公式 6-2 中 mH,Ein 和 Eout 还是有可能相差很大。 机器学习基本通过获取一个在 in-sample 上最小的 Ein 的 g , 并保证 Ein 和 Eout 在整个 hypothesis(要能选择算法) 足够PAC 相似。 如果用 2N 来代换公式 6-2 中的 mH, 那还是不能保证 Ein 和 Eout 足够地接近。
Breakpoint to The Rescue!对于某些 infinite hypothesis 存在 breakpoint K (K+1, K+2.... 也是 breakpoint), mH 要小于 2K。如图 6-2 所示,对于某些 infinite hypothesis 而言,它的 mH 是一个 polynomial 。这样的话,对于其它复杂的 infinite hypothesis, 能否找到一个 polynomial 上界呢?
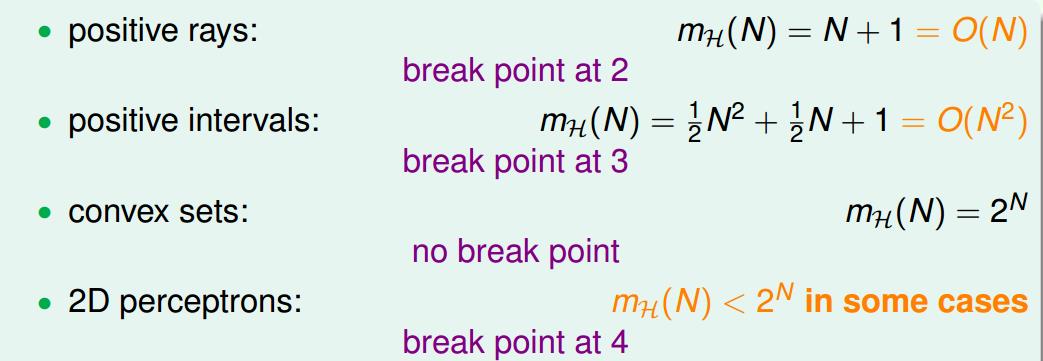
图 6-2
6.2 Bounding Function: Basic Cases
先定义一个新名词 bound function B(N, K): maximum possible mH(N) when break point = K。我们先用列表的方式来看下 B(N, K) 的关系。

图 6-3
先看一下 N = K 时, 因为 B(N,K) 肯定要小于 2K, 所以我们将 2K - 1 填上去(应该都能理解吧)。对于 K = 1 的情况,因为一个 hypothesis 所有的 h 将某一个 inputs 分类成一个。对于 N inputs 还是一样的, 所以 B(N,1)= 1。
6.3 Bounding Function:Inductive Cases
接着上一节,开始填充其它空白的地方。
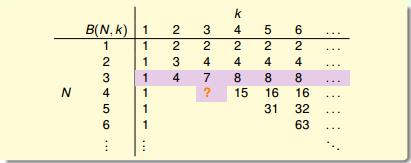
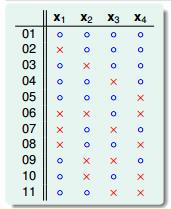
图 6-4 图 6-5
B(4,3)是多少? 写个程序枚举出 B(4,3) 是 11。可以看出 B(4,3) = B(3,3) + B(3,2) ,这不能说明什么。B(4,3) 和 B(3,?) 到底有什么关系?将图 6-5 重新排列一下得到图 6-6
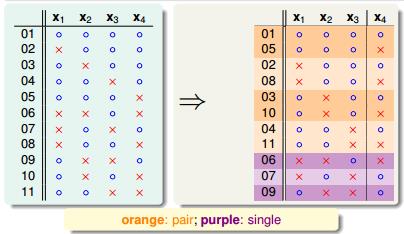
图 6-6
B(4,3) 有一部分是对称的, B(4,3) = 2α + β 。
去除 x4 , 只看 x1, x2, x3 这三点。因为 breakpoint 是 3, 所以 α + β ≤ B(3,3)。在已知 α + β 的上限情况下, 只要知道 α 的上限,我们就能知道 2α + β 的上限。
在 B(4,3) 中, break point 是 3。 所以 α 中任选 2 列都是可以完全可分的,那我们就从 α 中任选 2 列 plus 刚才去除的 x4 组成 3 列数据 γ。 因为 x4 是完全可以分,如果 γ 是完全可分的, 那么就会有问题, breakpoint 就不能是 3 了。 所以 3 个点的样本 α 肯定是不可分的,所以 α ≤ B(3,2)。 最终我们得出 B(4,3) ≤ B(3,3) + B(3,2)。
现在,我们可以填表了
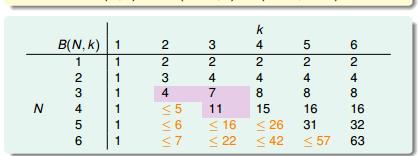
图 6-7
最终我们可以得出公式
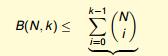
图 6-8
6.4 A Pictorial Proof
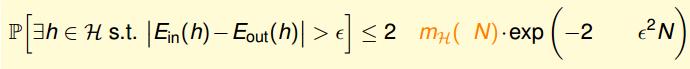
图 6-9
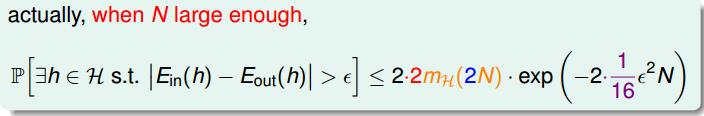
图 6-10
其实,我们还能得到一个更精确的 upper bound, 如 图 6-10 所示。 略过证明~
题外话
1. 感觉 6.1 讨论的话题在第 5 节就可以讨论了。没有按照 ppt 上来记笔记,有兴趣的同学可以去看杜少写的笔记
2. 以后不要截那么大的图
以上是关于机器学习基石笔记6——为什么机器可以学习的主要内容,如果未能解决你的问题,请参考以下文章