机器学习基石笔记15——机器可以怎样学得更好
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习基石笔记15——机器可以怎样学得更好相关的知识,希望对你有一定的参考价值。
转载请注明出处:http://www.cnblogs.com/ymingjingr/p/4271742.html
目录
机器学习基石笔记3——在何时可以使用机器学习(3)(修改版)
机器学习基石笔记16——机器可以怎样学得更好(4)
十五、Validation
验证。
15.1 Model Selection Problem
模型选择问题。
到目前为止,已经学过了许多算法模型,但一个模型需要很多参数的选择,这是本章讨论的重点。
以二元分类为例,在学过的算法有PLA、pocket、线性回归、logistic回归;算法中需要用到迭代方法,就需要选择迭代步骤T;同理也需要选择学习步长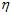 ;处理非线性问题时,需要用到不同的转换函数,可能是线性的,二次式,10次多项式或者10次勒让德多项式;如果加上正则化项,则可以选择L2正则化项,L1正则化项;有了正则化项,则参数
;处理非线性问题时,需要用到不同的转换函数,可能是线性的,二次式,10次多项式或者10次勒让德多项式;如果加上正则化项,则可以选择L2正则化项,L1正则化项;有了正则化项,则参数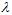 值也需要选择。
值也需要选择。
在如此多的选项中设计一个适用于各种情况各个数据集的模型显然是不可能的,因此针对不同的情况,对各个参数的选择是必须的。
选择的依据当然是在各种假设空间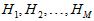 及各种算法
及各种算法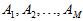 组成的模型中通过算法
组成的模型中通过算法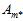 寻找到一个使得
寻找到一个使得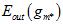 最小的
最小的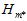 。但问题是不知道
。但问题是不知道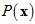 与
与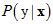 的情况下,即不知道
的情况下,即不知道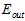 。
。
显然通过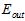 方式寻找最佳模型的方式行不通,通过寻找最小
方式寻找最佳模型的方式行不通,通过寻找最小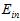 是否可行呢?如公式15-1所示。
是否可行呢?如公式15-1所示。
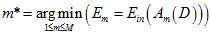 (公式15-1)
(公式15-1)
但是此举扔不合理,显然高次转换函数比低次转换函数得到的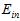 更小,加上正则化的比不加正则化的
更小,加上正则化的比不加正则化的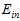 可能更大。
可能更大。
此种方式很容易产生过拟合现象,因此不好。
此外不同的算法A在不同的假设空间H中寻找各假设空间中使得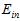 最小的假设函数g,将各假设函数g作对比,选择其中
最小的假设函数g,将各假设函数g作对比,选择其中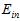 最小的作为
最小的作为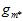 ,本质上是在各假设空间的联合空间中寻找
,本质上是在各假设空间的联合空间中寻找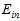 最小的
最小的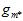 ,其VC维
,其VC维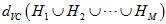 ,将有不好的泛化性能。
,将有不好的泛化性能。
训练数据集不行,那么使用测试数据集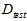 ,选择
,选择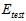 最小的假设函数,公式如15-2所示。
最小的假设函数,公式如15-2所示。
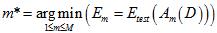 (公式15-2)
(公式15-2)
不同于使用训练数据,此种情况有霍夫丁不等式保证了泛化,如公式15-3所示。
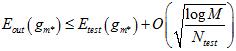 (公式15-3)
(公式15-3)
该霍夫丁不等式在7.4节给出了解释,其中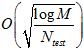 表示模型复杂度。但是这样做就正确了?实际上使用测试数据来选择模型参数是一种作弊的行为。
表示模型复杂度。但是这样做就正确了?实际上使用测试数据来选择模型参数是一种作弊的行为。
将以上两种方式进行对比,如表15-1所示。
表15-1 在选择参数时,使用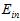 和
和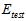 的对比
的对比
|
训练数据错误 |
测试错误 |
|
数据来自于训练数据D |
测试来自于测试数据 |
|
可行的(拥有该数据) |
不可行(没有该数据) |
|
被污染过了(训练数据决定了假设空间,不可再用来做参数选择) |
干净的 |
两种方式(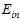 和
和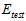 )都不好,因此设计一种中间的方法
)都不好,因此设计一种中间的方法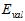 。将训练数据预留出一部分作为选择参数的验证(validation)数据,使用
。将训练数据预留出一部分作为选择参数的验证(validation)数据,使用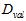 表示。此种数据是本身具有的,同时也是没受过污染的,使用确认数据寻找最小的
表示。此种数据是本身具有的,同时也是没受过污染的,使用确认数据寻找最小的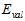 。
。
15.2 Validation
验证。
接着上一节提到的验证数据继续讲,为了达到数据既可用又不出现污染的情况,将原本的样本数据D分为两个部分:训练数据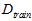 和验证数据
和验证数据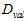 ,如公式15-4所示。
,如公式15-4所示。
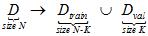 (公式15-4)
(公式15-4)
从原大样本数据集D得到的最佳函数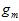 如公式15-5所示。
如公式15-5所示。
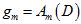 (公式15-5)
(公式15-5)
而从训练样本数据集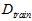 得到的最佳函数
得到的最佳函数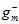 如公式15-6所示。
如公式15-6所示。
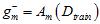 (公式15-6)
(公式15-6)
注意验证数据集是以联合概率分布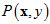 概率,独立同分布的从数据集D中抽取的K个样本。类似于上一节公式15-3,此处使用
概率,独立同分布的从数据集D中抽取的K个样本。类似于上一节公式15-3,此处使用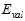 取代
取代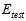 做测试,通过公式15-7做泛化保证。注意其中根号中分母的部分也换成了验证数据的数据量。
做测试,通过公式15-7做泛化保证。注意其中根号中分母的部分也换成了验证数据的数据量。
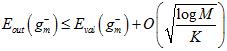 (公式15-7)
(公式15-7)
再总结下,使用此种方式的算法流程,如图15-1所示。
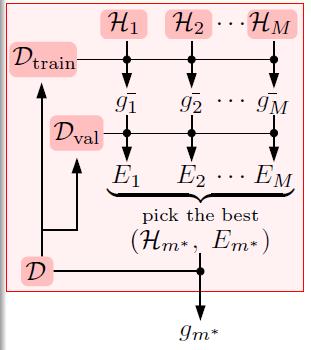
图15-1 使用训练数据集和验证数据集的算法流程
首先将原数据集D分为两部分:训练数据集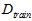 和验证数据集
和验证数据集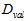 。不同的模型(不同的假设空间H和不同的算法A,算法中包括不同参数)用训练数据集
。不同的模型(不同的假设空间H和不同的算法A,算法中包括不同参数)用训练数据集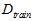 得到不同的最佳函数
得到不同的最佳函数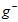 ,如图中各假设空间H得到的各最佳函数
,如图中各假设空间H得到的各最佳函数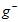 。再使用验证数据集
。再使用验证数据集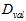 ,选择验证错误
,选择验证错误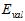 最小的,得出最佳模型,该过程可以写成公式15-8的形式。
最小的,得出最佳模型,该过程可以写成公式15-8的形式。
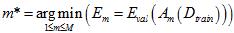 (公式15-8)
(公式15-8)
通过该模型训练整个数据集D,得到最终的假设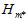 以及最小的
以及最小的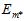 。注意最后是使用整个数据集D重新做的训练,而不是直接使用原本训练数据集
。注意最后是使用整个数据集D重新做的训练,而不是直接使用原本训练数据集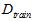 原本训练得到的结果,因为理论上数据量越大越接近最终的
原本训练得到的结果,因为理论上数据量越大越接近最终的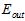 ,如公式15-9所示。
,如公式15-9所示。
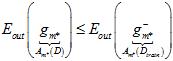 (公式15-9)
(公式15-9)
将公式15-7与公式15-9连接起来得公式15-10。
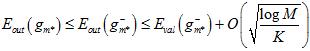 (公式15-10)
(公式15-10)
上述只是理论,甚至是直觉上得到的结论,以下是通过实验得到的数据绘制成图表,以表明不等式确实成立,如图15-2所示。图中横轴表示验证数据集的大小K,纵轴表示错误率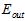 ,黑色虚线表示使用测试数据集
,黑色虚线表示使用测试数据集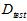 得到的最佳情况(现实中是不可能办到的);蓝色表示通过验证数据集算得的最佳模型号,再用整个样本集重新训练得到的最佳函数
得到的最佳情况(现实中是不可能办到的);蓝色表示通过验证数据集算得的最佳模型号,再用整个样本集重新训练得到的最佳函数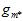 ;黑色直线表示使用整个样本集得到的最佳函数
;黑色直线表示使用整个样本集得到的最佳函数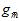 ;红色线表示直接通过训练样本得到的最佳函数
;红色线表示直接通过训练样本得到的最佳函数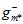 。从该图也可以得到
。从该图也可以得到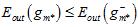 的结论。
的结论。
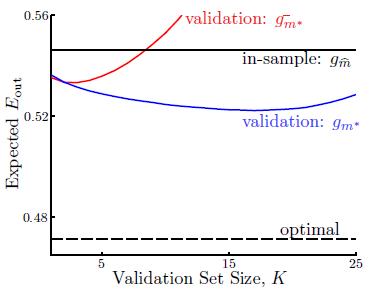
图15-2 验证数据集的可行性
解释下为何红色线在验证样本大于一定数量时变得越来越差,,原因是样本总是是固定的,当验证样本增加时,训练样本变得越来越小,因此得到的假设函数越来越差。
注意公式15-10有两个近似关系,其中当K足够大时,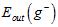 与
与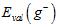 越接近,但是因为N-K在变小,导致
越接近,但是因为N-K在变小,导致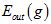 与
与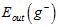 相差更大;同理当K足够小时,
相差更大;同理当K足够小时, 与
与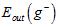 足够接近,但是
足够接近,但是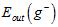 与
与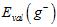 相差很大。K的选择成为了一个新的问题,林老师推荐K的选择为
相差很大。K的选择成为了一个新的问题,林老师推荐K的选择为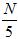 。
。
15.3 Leave-One-Out Cross Validation
留一法交叉验证。
上一节中提到K的取值很重要,假设一种极端的情况K=1,即验证数据集为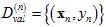 ,则验证错误率为
,则验证错误率为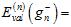
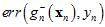
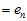 。如何使得
。如何使得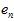 更接近
更接近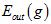 ,使用留一法交叉验证(Leave-One-Out Cross Validatio),其公式如15-11。
,使用留一法交叉验证(Leave-One-Out Cross Validatio),其公式如15-11。
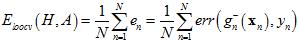 (公式15-11)
(公式15-11)
看公式可能会觉得复杂,接着说明如何使用留一法交叉验证。假设有三个样本点和两种模型:线性模型和常数模型,其结果如图15-3和图15-4所示。
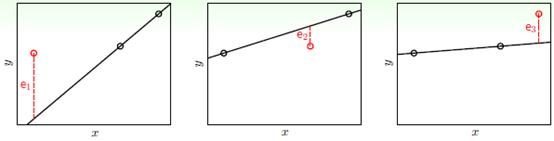
图15-3 线性模型留一法交叉验证
线性模型留一法交叉验证的求解公式如公式15-12所示。
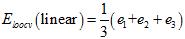 (公式15-12)
(公式15-12)
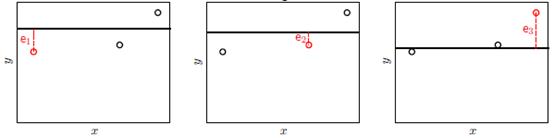
图15-4常数模型留一法交叉验证
常数模型留一法交叉验证的求解公式如公式15-13所示。
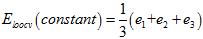 (公式15-13)
(公式15-13)
通过公式15-14选择最佳的模型。
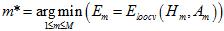 (公式15-14)
(公式15-14)
从公式15-12到公式15-14可得常数模型比线性模型错误率更小,这个结果体现降低复杂度的思想。
最重要的问题是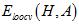 是否接近
是否接近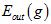 ?以下从理论的角度推导在样本数量为N-1时,平均
?以下从理论的角度推导在样本数量为N-1时,平均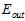 与
与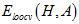 的关系。
的关系。
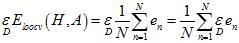
(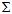 与
与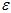 都是线性函数,因此可以调换位置。)
都是线性函数,因此可以调换位置。)
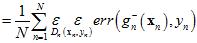
(可以将样本数据集拆为去除验证样本后的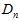 和单一验证样本
和单一验证样本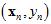 ,而
,而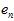 也写成其真正的形式
也写成其真正的形式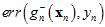 )
)
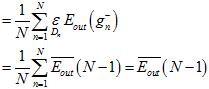 (公式15-14)
(公式15-14)
因此证明了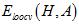 与
与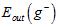 (就是
(就是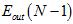 )接近,而
)接近,而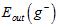 与
与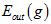 又几乎一致,因为只差了一个样本。
又几乎一致,因为只差了一个样本。
理论上证明留一法交叉验证有效可能还是比较抽象,以下从实验角度,以手写数字集为例,如图15-5所示,蓝色表示为"1"的样本,红色表示非"1"样本,以对称性(symmetry)和密度(intensity)为样本的特征值,中间的一幅图为以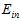 作为依据得到的最优函数划分,明显很不平滑,右图为以
作为依据得到的最优函数划分,明显很不平滑,右图为以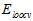 为依据得到的最优函数划分,平滑很多。
为依据得到的最优函数划分,平滑很多。
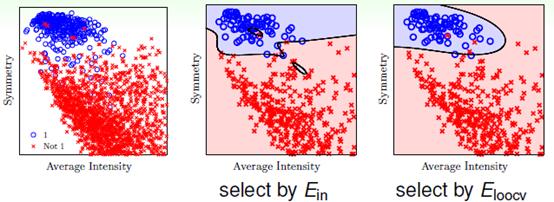
图 15-5 手写数据集表明留一法交叉验证的效果
而通过实验绘制了特征数量(即模型的复杂度,特征越多模型越复杂)与各错误率(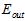 、
、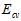 及
及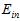 )之间的关系图。如图15-6所示。
)之间的关系图。如图15-6所示。
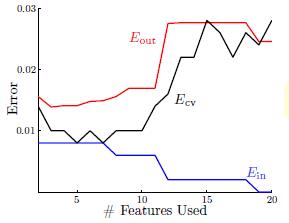
图15-6 特征数量与各错误率之间的关系图
从图中不难得出,随着模型复杂度提高,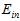 不断降低(因为更高次的函数拟合样本点),与实际的
不断降低(因为更高次的函数拟合样本点),与实际的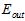 相差越来越大;同时
相差越来越大;同时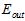 则在不断增加;而
则在不断增加;而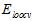 和
和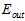 的曲线非常接近。因此
的曲线非常接近。因此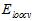 比
比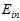 好得多。
好得多。
15.4 V-Fold Cross Validation
K-折交叉验证。
上一节中介绍的留一法交叉验证存在两个问题,一是当数据量稍大时选择模型的成本多大,比如样本为1000个,则每个模型要使用999个样本运行1000次,因此在实际运用中可用性不高;二是稳定性不好,因为总是单一样本做验证,导致如图15-6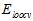 曲线的曲线波动性过大,很不稳定。实际应用中很少使用留一法交叉验证。
曲线的曲线波动性过大,很不稳定。实际应用中很少使用留一法交叉验证。
为了解决留一法交叉验证的两个问题,提出了一种交叉验证方式,将样本数据集分成V个大小相等的部分,选择其中V-1个部分做训练,其中一部分做验证。交叉错误如公式15-15所示。
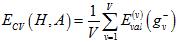 (公式15-15)
(公式15-15)
选择最优模型的公式如公式15-16所示。
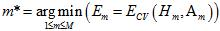 (公式15-16)
(公式15-16)
林老师推荐V的选择为10。
以上是关于机器学习基石笔记15——机器可以怎样学得更好的主要内容,如果未能解决你的问题,请参考以下文章