BZOJ 2179: FFT快速傅立叶

Posted 2020-10-17 ZlycerQan

二次联通门 : BZOJ 2179: FFT快速傅立叶

 

权限题放题面

 

 

 

 

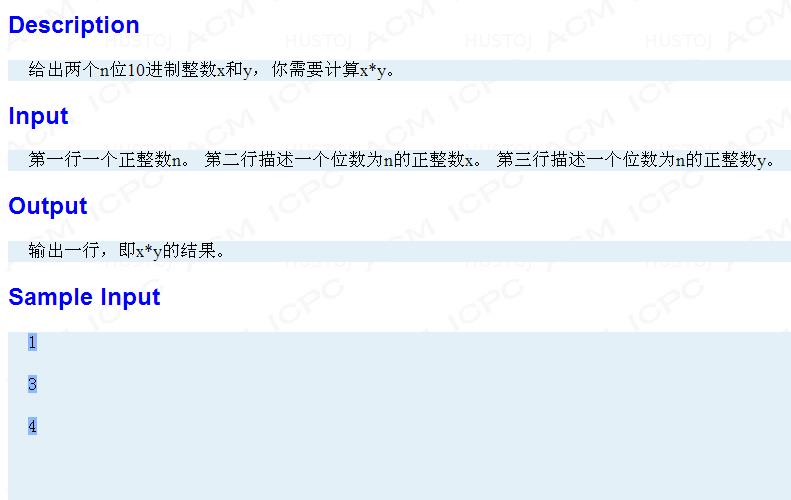
#include <cstdio>
#include <iostream>
#include <cmath>

#define Max 1000005
#define rg register
typedef double flo;
struct vec 
{
    flo x, y; vec (flo a = 0, flo b = 0) : x (a), y (b) { }

    vec operator + (const vec &rhs)
    { return vec (x + rhs.x, y + rhs.y); }

    vec operator - (const vec &rhs)
    { return vec (x - rhs.x, y - rhs.y); }

    vec &operator /= (const flo &k)
    { return x /= k, y /= k, *this; }

    vec operator * (const vec &rhs)
    { return vec (x * rhs.x - y * rhs.y, x * rhs.y + y * rhs.x); }

} a[Max], b[Max];
int rd[Max];
char s[Max];
const flo PI = acos (-1.0);
void DFT (vec *a, int N, int f = 1)
{
    rg int i, j, k; vec wn, w, x, y;
    for (i = 0; i < N; ++ i) if (rd[i] > i) std :: swap (a[i], a[rd[i]]);

    for (k = 1; k < N; k <<= 1)
    {
        wn = vec (cos (PI / k), f * sin (PI / k));
        for (j = 0; j < N; j += k << 1)
            for (i = 0, w = vec (1, 0); i < k; ++ i, w = w * wn)
                x = a[j + i], y = w * a[i + j + k], a[i + j] = x + y, a[i + j + k] = x - y;
    }    
    if (f == -1) for (i = 0; i < N; ++ i) a[i] /= N;
}
void FFT (vec *a, vec *b, int N)
{
    int p = N << 1, L = 0; rg int i;
    for (N = 1; N <= p; N <<= 1) ++ L;
    for (i = 0; i < N; ++ i)
        rd[i] = (rd[i >> 1] >> 1) | ((i & 1) << (L - 1));
    DFT (a, N), DFT (b, N);
    for (i = 0; i <= N; ++ i) a[i] = a[i] * b[i];
    DFT (a, N, -1);
}
int c[Max];
int main (int argc, char *argv[])
{
    int N; scanf ("%d", &N); -- N; rg int i;
    scanf ("%s", s);
    for (i = 0; i <= N; ++ i) a[i].x = s[N - i] - \'0\';
    scanf ("%s", s);
    for (i = 0; i <= N; ++ i) b[i].x = s[N - i] - \'0\';
    FFT (a, b, N);
    int p = N * 2;
    for (i = 0; i <= p; ++ i) c[i] = (int) (a[i].x + 0.5);
    for (i = 0; i <= p; ++ i)
        if (c[i] >= 10)
        {
            c[i + 1] += c[i] / 10, c[i] %= 10;
            if (i == p) ++ p;
        }
    for (; c[p] == 0; -- p);
    for (i = p; i >= 0; -- i) printf ("%d", c[i]);
    putchar (\'\\n\');
    return 0;
}