二分图匹配

Posted 2020-10-17 H

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二分图匹配相关的知识，希望对你有一定的参考价值。

　　这两个星期一直没什么时间上机，最近学了学二分图，这里就来记录一下。

------------------------------------------------------------分割线

　　先讲讲一些基本概念：

　　二分图：在一个图中，如果图中的点可以被分为两个部分，两部分之间有若干条边相连，且每个部分的点之间无边相连，则该图是一个二分图。由此可以很容易知道，二分图绝对是一个无环图。

　　匹配：图论中，一个“匹配”是一个边的集合，其中任意两条都没有公共定点。由此衍生出一些其他的概念，匹配点，匹配边，未匹配点，未匹配边，定义显而易见就不多赘述了。

　　最大匹配：一个二分图中包含的边数最大的一个匹配就是这个二分图的最大匹配。一般二分图的问题经常会涉及到最大匹配，所以这也是学习二分图的一个重点。

　　完美匹配：如果在一个二分图中，存在一个匹配使得所有点都是匹配点，则这个匹配称为这个二分图的完美匹配。可知，一个二分图的完美匹配一定也是这个二分图的一个最大匹配。

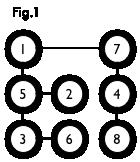
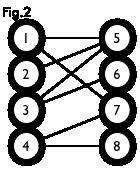
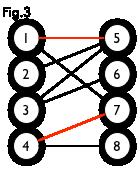
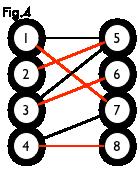
　　 Bipartite Graph(1) Bipartite Graph(2) Matching Maximum Matching

　　如上图，图一是一个二分图，但从外表并不明显，可以转换成图二的样式。图三是这个二分图的一个匹配（红线部分），图四则是它的最大匹配，也是完美匹配。

　　讲完基本概念，来说说解决二分图最大匹配的常用算法——匈牙利算法。

　　首先讲讲两个概念，交替路和增广路。

　　如右图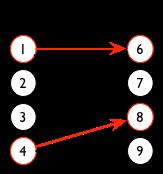

　　交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

　　增广路：从一个未匹配点出法，走交替路，如果途径一个未匹配点（非出发点），则该条交替路称为一个增广路。如下图是上图的一个增广路展开后的情况

　　由这两个概念可以知道，如果一个二分图中存在增广路则最大匹配一定比当前找到的匹配大。如上图，找到的增广路中有两条匹配边4-8和1-6，则现在可以增加为三条9-4和8-1和6-2。匈牙利算法的主体思想大致就是这样，不停地寻找增广路，如果可以找到，则当前答案ans++，直到找不到增广路为止，正确性很容易证明。

　　一般匈牙利算法有BFS和DFS两种方法。下面放上洛谷模板题的dfs算法：

#include<bits/stdc++.h>
using namespace std;

const int N=2019;
const int M=2e6+7;
int n,m,E,head[N],cnte,mc[N],ans;
bool vis[N];
struct Edge { int to,nxt; }e[M];

inline int read()
{
    int x=0; char ch=getchar();
    while( ch<\'0\' || ch>\'9\' ) ch=getchar();
    while( ch>=\'0\' && ch<=\'9\' ) {
        x=x*10+ch-\'0\'; ch=getchar();
    }
    return x;
}

inline void add(int x,int y)
{
    e[++cnte].to=y;
    e[cnte].nxt=head[x];
    head[x]=cnte;
}

bool dfs(int x)
{
    int y;
    for(int i=head[x]; i!=-1; i=e[i].nxt) {
        y=e[i].to;
        if( vis[y] ) continue;
        vis[y]=1;
        if( mc[y]==-1 || dfs(mc[y]) ) {
            mc[x]=y, mc[y]=x;
            return 1;    
        }
    }
    return 0;
}

int main()
{
    n=read(), m=read(), E=read();
    memset(head,-1,sizeof(head));
    int x,y;
    for(int i=1; i<=E; ++i) {
        x=read(), y=read();
        if( x>n || y>m ) continue;
        add(x,y+n), add(y+n,x);
    }
    memset(mc,-1,sizeof(mc));
    for(int i=1; i<=n; ++i) {
        if( mc[i]!=-1 ) continue;
        memset(vis,0,sizeof(vis));
        if( dfs(i) ) ans++;
    }
    return printf("%d\\n",ans),0;
}