别被看似简单的羊车门问题绕进去

Posted 2020-10-11 张鹏yu

首先看一下问题：

 

有3扇关闭的门，一扇门后面停着汽车，其余门后是山羊，只有主持人知道每扇门后面是什么。参赛者可以选择一扇门，在开启它之前，主持人会开启另外一扇门，露出门后的山羊，然后允许参赛者更换自己的选择。

 

第一眼看到觉得并没有那么简单，但是说实话，第一选择是换不换都一样，因为我认为主持人又不是随机开的，换不换都一样。而且最好别换，因为用玄学解释，最好不要随意更换自己最初的选择。

经过讨论和百度，我们开始认为换比较好，但是大家也没有得出统一的概率值，网上也各种说法都有，所以我谈谈我的理解，不换概率永远是1/3，换了选择车的概率可能更大。但我觉得是1/2，同伴不同意，我们就决定用Python验证一下。

思路如下：

不换：选完以后不再管了。

换：选完之后改变自己的选择。

因为不换的话，第一次需要选中车，概率就是1/3.这个就不用验证了，主要验证一下换了之后是车的概率。

我们直接进行1000次试验。如果一开始选择的是车，那么就完了，如果一开始选择的是羊，那就中了。这里面比较迷惑的是主持人开了个门，把这个弄明白就可以了，首先他开的肯定不是你选择的门，而且他开的是羊。就是说，这是一个干扰项，没什么意义，因为他不会对选择造成干预。所以代码只需要看他第一次选择的是车还是羊就行了，其实理解之后也用不到代码了，不过还是验证一下。

代码如下，用了循环和条件。

import random
x=1000
zhong=0
buzhong=0
i=0
car=random.randint(1,3)
for i in range(x):
    choice=random.randint(1,3)
    if choice==car:
        buzhong=buzhong+1
    else:
        zhong=zhong+1
print(\'换了之后不中的概率:{}\'.format(buzhong/x))
print(\'换了之后中的概率:{}\'.format(zhong/x))

得出的结果如下

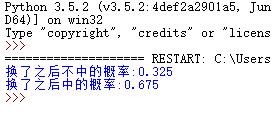
所以还是换比较好。

结组成员：张鹏宇，刘冰倩