数据结构与算法(周鹏-未出版)-第六章 树-6.2 二叉树

Posted 2020-10-10 crazyYong

6.2 二叉树

在进一步讨论树的存储结构及其操作之前，先讨论一种简单而极其重要的树结构—二叉树。因为任何树都可以转化为二叉树进行处理，并且二叉树适合计算机的存储和处理，因此在本章中二叉树是研究的重点。

 

6.2.1 二叉树的定义

 

每个结点的度均不超过 2 的有序树，称为二叉树（ binary tree）。

与树的递归定义类似，二叉树的递归定义如下：二叉树或者是一棵空树，或者是一棵由一个根结点和两棵互不相交

的分别称为根的左子树和右子树的子树所组成的非空树。

由以上定义可以看出，二叉树中每个结点的孩子数只能是 0、 1 或 2 个，并且每个孩子都有左右之分。位于左边的孩子称为左孩子，位于右边的孩子称为右孩子；以左孩子为根的子树称为左子树，以右孩子为根的子树称为右子树。

 

与树的基本操作类似，二叉树有如下基本操作：

 

6.2.2 二叉树的性质

 

在二叉树中具有以下重要性质。

 

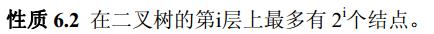
该性质易由数学归纳法证明。证明略。由性质 6.2 可以得到如下的进一步结论：

下面介绍两种特殊的二叉树，然后讨论其有关性质。

 

 

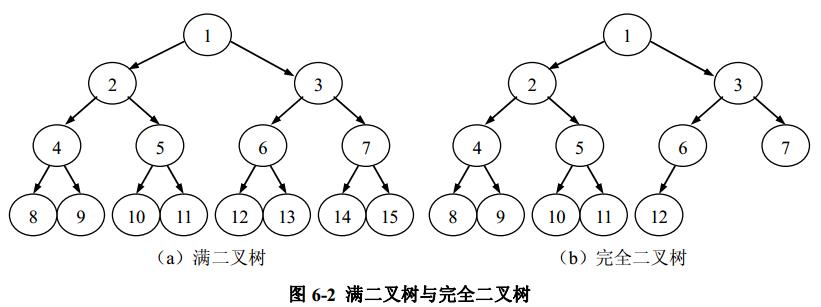
　　可以对满二叉树的结点进行编号，约定编号从根结点起，层间自上而下，层内自左而右，逐层由 1 到 n 进行标号。

如果按照上述对满二叉树结点编号的方法，对具有 n 个结点的完全二叉树中结点进行编号，那么完全二叉树中 1~ n 号结点的位置与满二叉树中 1~ n 号结点的位置是一致的。图 6-2（ b）所示的二叉树就是一棵完全二叉树。

 

可见，满二叉树必为完全二叉树，而完全二叉树不一定是满二叉树。

 

 

6.2.3 二叉树的存储结构

二叉树的存储结构有两种：顺序存储结构和链式存储结构。

 

@顺序存储结构

对于满二叉树和完全二叉树来说，可以将其数据元素逐层存放到一组连续的存储单元中，如图 6-3 所示。用一维数组来实现顺序存储结构时，将二叉树中编号为 i 的结点存放到

数组中的第 i 个分量中。如此根据性质 6.7，可以得到结点 i 的父结点、左右孩子结点分别存放在[2/i] 、2i 以及 2i+1 分量中。

 

这种存储方式对于满二叉树和完全二叉树是非常合适也是高效方便的。因为满二叉树和完全二叉树采用顺序存储结构既不浪费空间，也可以根据公式很快的确定结点之间的关系。但是对于一般的二叉树而言，必须用“虚结点”将一棵二叉树补成一棵完全二叉树来存储，否则无法确定结点之间的前驱后续关系，但是这样一来就会造成空间的浪费。一种极端的情

况是，为了存储k个结点，需要 个存储单元，图 6- 4 说明了这一情况。此时存储空间浪费巨大，这是顺序存储结构的一个缺点。

@链式存储结构

设计不同的结点结构可构成不同的链式存储结构。在二叉树中每个结点都有两个孩子，则可以设计每个结点至少包括 3 个域： 数据域、左孩子域和右孩子域。数据域存放数据元素，左孩子域存放指向左孩子结点的指针，右孩子域存放指向右孩子结点的指针。如图 6-5（ a）所示。利用此结点结构得到的二叉树存储结构称为二叉链表。容易证明在具有 n 个结点的二

叉链表中有 n+1 个空链域。

 

为了方便找到父结点，可以在上述结点结构中增加一个指针域，指向结点的父结点。如图 6-5（ b）所示。采用此结点结构得到的二叉树存储结构称为三叉链表。在具有 n 个结点的三叉链表中也有 n+1 个空链域。

不同的存储结构实现二叉树操作的方法也不同。例如要找某个结点的父结点，在三叉链表中很容易实现；在二叉链表中则需从根结点出发一一查找。在实际应用中，要根据二叉树的主要操作来选择存储结构。为了方便的找到父结点，我们以三叉链表作为二叉树的存储结构，并且在 6.3 节中，二叉树的基本操作的实现也是基于三叉链表来实现的。下面我们首先给出具有四个域的结点结构的定义。

 

代码 6-1 二叉树存储结构结点定义

public class BinTreeNode implements Node {
private Object data; //数据域
private BinTreeNode parent; //父结点
private BinTreeNode lChild; //左孩子
private BinTreeNode rChild; //右孩子
private int height; //以该结点为根的子树的高度
private int size; //该结点子孙数（包括结点本身）
102
public BinTreeNode() { this(null); }
public BinTreeNode(Object e) {
data = e; height = 0; size = 1;
parent = lChild = rChild = null;
}
/******Node 接口方法******/
public Object getData() { return data; }
public void setData(Object obj) { data = obj;}
/******辅助方法,判断当前结点位置情况******/
//判断是否有父亲
public boolean hasParent(){ return parent!=null;}
//判断是否有左孩子
public boolean hasLChild(){ return lChild!=null;}
//判断是否有右孩子
public boolean hasRChild(){ return rChild!=null;}
//判断是否为叶子结点
public boolean isLeaf(){ return !hasLChild()&&!hasRChild();}
//判断是否为某结点的左孩子
public boolean isLChild(){ return (hasParent()&&this==parent.lChild);}
//判断是否为某结点的右孩子
public boolean isRChild(){ return (hasParent()&&this==parent.rChild);}
/******与 height 相关的方法******/
//取结点的高度,即以该结点为根的树的高度
public int getHeight() { return height; }
//更新当前结点及其祖先的高度
public void updateHeight(){
int newH = 0;//新高度初始化为 0,高度等于左右子树高度加 1 中的大者
if (hasLChild()) newH = Math.max(newH,1+getLChild().getHeight());
if (hasRChild()) newH = Math.max(newH,1+getRChild().getHeight());
if (newH==height) return; //高度没有发生变化则直接返回
height = newH; //否则更新高度
if (hasParent()) getParent().updateHeight(); //递归更新祖先的高度
}
/******与 size 相关的方法******/
//取以该结点为根的树的结点数
public int getSize() { return size; }
//更新当前结点及其祖先的子孙数
public void updateSize(){
size = 1; //初始化为 1,结点本身
if (hasLChild()) size += getLChild().getSize(); //加上左子树规模
103
if (hasRChild()) size += getRChild().getSize(); //加上右子树规模
if (hasParent()) getParent().updateSize(); //递归更新祖先的规模
}
/******与 parent 相关的方法******/
//取父结点
public BinTreeNode getParent() { return parent; }
//断开与父亲的关系
public void sever(){
if (!hasParent()) return;
if (isLChild()) parent.lChild = null;
else parent.rChild = null;
parent.updateHeight(); //更新父结点及其祖先高度
parent.updateSize(); //更新父结点及其祖先规模
parent = null;
}
/******与 lChild 相关的方法******/
//取左孩子
public BinTreeNode getLChild() { return lChild; }
//设置当前结点的左孩子,返回原左孩子
public BinTreeNode setLChild(BinTreeNode lc){
BinTreeNode oldLC = this.lChild;
if (hasLChild()) { lChild.sever();} //断开当前左孩子与结点的关系
if (lc!=null){
lc.sever(); //断开 lc 与其父结点的关系
this.lChild = lc; //确定父子关系
lc.parent = this;
this.updateHeight(); //更新当前结点及其祖先高度
this.updateSize(); //更新当前结点及其祖先规模
}
return oldLC; //返回原左孩子
}
/******与 rChild 相关的方法******/
//取右孩子
public BinTreeNode getRChild() { return rChild; }
//设置当前结点的右孩子,返回原右孩子
public BinTreeNode setRChild(BinTreeNode rc){
BinTreeNode oldRC = this.rChild;
if (hasRChild()) { rChild.sever();} //断开当前右孩子与结点的关系
if (rc!=null){
rc.sever(); //断开 lc 与其父结点的关系
this.rChild = rc; //确定父子关系
104
rc.parent = this;
this.updateHeight(); //更新当前结点及其祖先高度
this.updateSize(); //更新当前结点及其祖先规模
}
return oldRC; //返回原右孩子
}
}

 

代码 6-1 说明：代码中判断当前结点位置情况的辅助方法以及简单的 get 方法都在常数时间内可以完成，实现也相应非常简单。下面主要讨论 updateHeight ()、 updateSize ()、 sever()、setLChild(lc)、 getRChild(rc)的实现与时间复杂度。

 

⑴ updateHeight ()：若当前结点 v 的孩子发生变化，就需要使用 updateHeight ()方法更新当前结点及其祖先结点的高度。请注意，由于一个结点的高度发生变化，会影响到其祖先结点的高度，在这里我们允许直接对任何结点执行这一操作。

因为在二叉树中任何一个结点的高度，都等于其左右子树的高度中大者加 1，而左右子树的高度只需要获取该结点左右孩子的高度即可获得，只需要Θ (1)时间。续而从 v 出发沿parent 引用逆行向上，依次更新各祖先结点的高度即可。如果在上述过程中，发现某个结点的高度没有发生变化，算法可以直接终止。综上所述，当对一个结点 v 调用 updateHeight ()

方法时，若 v 的层数为 level(v)，则最多只需要更新 level(v)+1 个结点的高度，因此算法的时间复杂度 T(n) = Ο (level(v))。

 

⑵ updateSize ()：同样如果结点 v 的孩子发生变化，应该更新当前结点以及其祖先的规模。因为在二叉树中任何一个结点的规模，都等于其左右子树的规模之和加上结点自身，而左右子树的规模只需要获取该结点左右孩子的规模即可获得，只需要Θ (1)时间。因此算法的时间复杂度 T(n) = Ο (level(v))。

 

⑶ sever()：切断结点 v 与父结点 p 之间的关系。该算法需要修改 v 与 p 的指针域，需要常数时间。除此之外由于 p 结点的孩子发生了变化，因此需要调用 updateHeight ()和updateSize ()来更新父结点 p 及其祖先的高度与规模。其时间复杂度 T(n) = Ο (level(v))。

 

⑷ setLChild(lc)、 getRChild(rc)：两个算法的功能相对，一个是设置结点 v 的左孩子，一个是设置结点 v 的右孩子。两个算法的实现是类似的，以 setLChild()为例说明。首先，如果 v 有左孩子 oldLC，则应当调用 oldLC. sever()断开 v 与其左孩子的关系。 其次， 调用 lc. sever()断开其与父结点的关系。最后，建立 v 与 lc 之间的父子关系，并调用 v. updateSize ()与 v.updateHeight ()更新 v 及其祖先的规模与高度。