数据结构与算法(周鹏-未出版)-第六章 树-6.4 树森林

Posted 2020-10-10 crazyYong

6.4 树、森林

在介绍二叉树之后，我们回到树的存储及其操作的实现中来。

6.4.1 树的存储结构

树的存储结构主要有以下三种。

„@双亲表示法
设 T 是一棵树，表示 T 的一种最简单的方法是用一个一维数组存储每个结点，数组的下标就是结点的位置指针，每个结点中有一个指向各自的父亲结点的数组下标的域。由于树中每个结点的父亲是唯一的，所以上述的父亲数组表示法可以唯一地表示任何一棵树。图6-8 说明了这种存储结构。对于树的这种存储结构的结点结构定义，请读者自行给出。

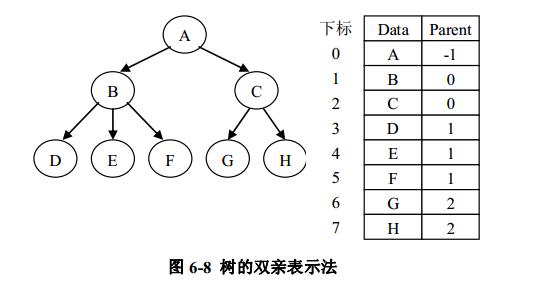
　　在这种表示法下，寻找一个结点的父结点只需要 O(1)时间。在树中可以从一个结点出发找出一条向上延伸到达其祖先的路径，即从一个结点到其父亲，再到其祖父等等。求这样的路径所需的时间正比于路径上结点的个数。在树的父亲数组表示法中，对于涉及查询儿子和兄弟信息的树操作，可能要遍历整个数组。为了节省查询时间，可以规定指示儿子的数组下标值大于父亲的数组下标值，而指示兄弟结点的数组下标值随着兄弟的从左到右是递增的，即如图 6-8

 

@孩子链表表示法

　　树的另一种常用的表示方法就是孩子链表表示法。这种表示法用一个线性表来存储树的所有结点信息，称为结点表。对每个结点建立一个孩子表。孩子表中只存储孩子结点的地址信息，可以是指针，数组下标甚至内存地址。由于每个结点的孩子数目不定，因此孩子表常用单链表来实现，因此这种表示法称为孩子链表表示法。图 6-9 是一个孩子链表表示法的示意图。

　　图 6-9（ b）中孩子链表结构表示的树如图 6-9（ a）所示，树中各结点存放于一个数组实现的表中，数组下标作为各结点的指针。每一个数组元素（即每一个结点）含有一个孩子表，在图 6-9（ b）中孩子表是用单链表来实现的，当然也可以用其他表的实现方式来实现孩子表。但由于每个结点的孩子数目不确定，所以一般不用数组来实现孩子表，但可以用数组来实现结点表，就如图 6-9（ b）所示。在图 6-9（ b）中可以看到，位于结点表第一个位置的结点有两个孩子结点，从左到右的两个孩子结点分别位于结点表的第 2 和第 3 个位置。因为图 6-9（ b）中的结点表用数组实现，所以结点的标号就是结点在结点表中的数组下标，即1和2

 

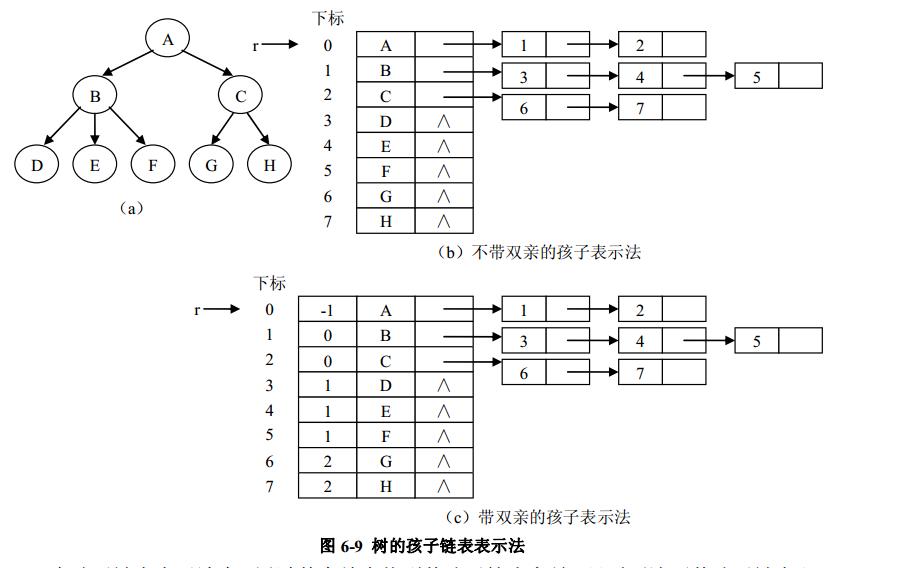
　　在孩子链表表示法中，通过某个结点找到其孩子较为容易，只需要遍历其孩子链表即可找到其所有孩子结点，然而要找到某个结点的父结点却需要对每个结点的孩子链表进行遍历，比较麻烦。因此可以在孩子链表表示法的基础上结合双亲表示法，在每个结点中再附设一个指示双亲结点的域，这样就可以在 O(1)时间内找到父结点。如图 6-9（ c）所示。

 

@孩子兄弟表示法
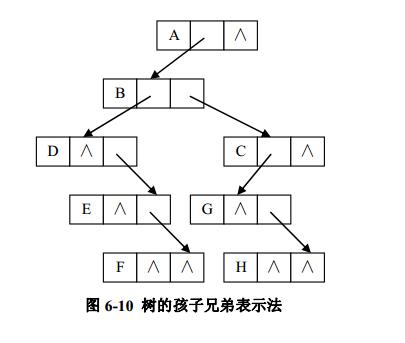
　　树的孩子兄弟表示法又称为二叉树表示法。每个结点除了 data 域外，还含有两个域，分别指向该结点的第一个孩子和右邻兄弟。图6-10 是图 6-9（ a）中所示树的孩子兄弟表示法。在图 6-10 中是使用二叉链表进行存储，这种结构便于实现树的各种操作。如果在二叉链表的每个结点中多增设一个 parent 域，则同样可以方便地实现查找父结点的操作。

 

 

6.4.2 树、森林与二叉树的相互转换

　　在上一小节介绍了树的存储结构，通过树的孩子兄弟表示法可以看到，树和二叉树都可以使用二叉链表作为存储结构。则以二叉链表可以导出树与二叉树之间的一个对应关系。也就是说给出一棵树可以将其唯一地对应到一棵二叉树，从实际的存储结构来看，它们的二叉链表是相同的，只是解释不同而已。图 6-11 展示了一个树与二叉树对应关系的例子。

 

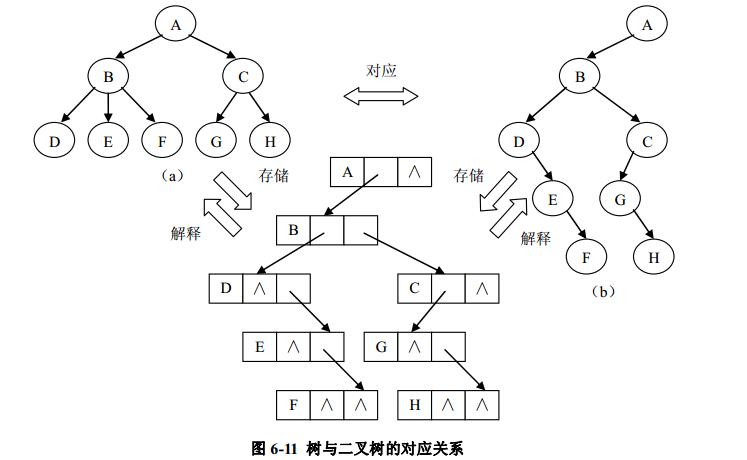
　　从树的孩子兄弟表示法的定义知道，任何一棵和某个树相对应的二叉树，其右子树必为空。

　　下面我们给出将一棵树转换为二叉树的方法：

　　将树中每个结点的第一个孩子转化为二叉树中对应结点的左孩子，将该结点右边的第一个兄弟转化为二叉树中该结点的右孩子。这实际上就是树的孩子兄弟表示法。
森林是若干棵树的集合。树可以转换为二叉树，森林同样也可以转换为二叉树。因此，森林也可以方便的使用孩子兄弟链表表示。森林转换为二叉树的方法是：

① 将森林中的每一棵树转换为相应的二叉树。

② 将所得的第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子。由以上两个步骤得到的二叉树就是森林转换得到的二叉树。例如图 6-12 展示了森林与二叉树之间的对应关系。

 

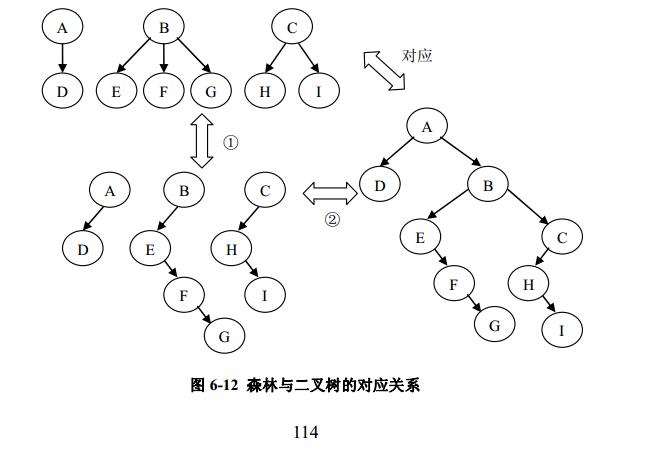
　　森林和树都可以转换为二叉树，二者的不同是：树转换为二叉树，其根结点的右子树必然为空；而森林转换为二叉树后，其根结点有右孩子（不考虑森林退化为树和森林与树为空的情况）。

将一棵二叉树还原为树或森林，具体方法如下：按层次序列对二叉树中每个结点做如下操作

① 如果是根结点或者是左孩子结点，那么不做任何改动；

② 如果是右孩子将其父结点设置为其当前父亲的父亲，若其当前父亲的父亲为空，则改动后其父亲为空。

 

 

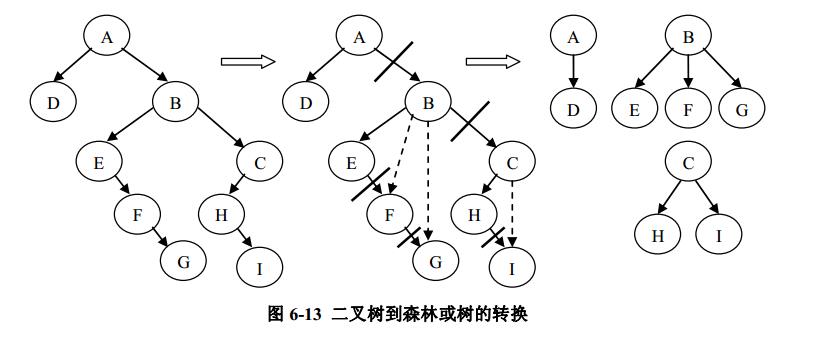
　　这种对应关系导致森林或树与二叉树之间可以相互转换，这种相互转换可以进行递归的形式定义。

 

6.4.3 树与森林的遍历

树的遍历
由树的定义可以得到两种次序遍历树的方法：

⑴ 先根遍历
若树非空，则遍历方法为：
① 访问树的根结点，
② 从左到右，依次先根遍历根的每棵子树。

例如图 6-11（ a）中树的先根遍历序列为： ABDEFCGH

⑵ 后根遍历
若树非空，则遍历方法为：
① 从左到右，依次后根遍历根的每棵子树，
② 访问树的根结点。
例如图 6-11（ a）中树的后根遍历序列为： DEFBGHCA

 

 森林的遍历
森林的遍历可以有以下三种方法：

⑴ 先序遍历
若森林非空，则：
① 访问森林中第一棵树的根结点；
② 先序遍历第一棵树中根结点的子树森林；
③ 先序遍历除去第一棵树后剩余的树构成的森林。
例如图 6-13 中森林的先序遍历序列为： ADBEFGCHI

⑵ 中序遍历
若森林非空，则：
① 中序遍历第一棵树中根结点的子树森林；
② 访问森林中第一棵树的根结点；
③ 中序遍历除去第一棵树后剩余的树构成的森林。

例如图 6-13 中森林的中序遍历序列为： DAEFGBHIC

⑶ 后序遍历
若森林非空，则：
① 后序遍历第一棵树中根结点的子树森林；
② 后序遍历除去第一棵树后剩余的树构成的森林；
③ 访问森林中第一棵树的根结点。

　　例如图 6-13 中森林的后序遍历序列为： DGFEIHCBA对照二叉树与森林之间的转换方法可以发现，森林的先序、中序、后序遍历与其相对应的二叉树的先序、中序、后序遍历的结果是相同的，因此可以用相应二叉树的遍历来验证森林的遍历结果。另外树可以看成只有一棵树的森林，所以树的先根遍历和后根遍历可以分别与森林的先序遍历和中序遍历对应，因此也就可以对应为相应二叉树的先序和中序遍历。
　　由此可见，当以二叉链表作为存储结构时，树的先根遍历和后根遍历可以借助相应二叉树的先序遍历和中序遍历的算法实现。

 

 6.4.4 由遍历序列还原树结构

 

　　前面我们介绍了由二叉树、树、森林等逻辑结构按照不同的次序得到相应结构的遍历序列。那么通过遍历序列是否可以还原相应的逻辑结构呢？

　　我们只分析二叉树的遍历序列还原为二叉树的问题。由于森林（包括树）的各种遍历可以对应为相应二叉树的遍历，如果通过遍历序列能还原为二叉树，也就可以相应的还原为森林。

　　首先通过二叉树的一种遍历序列是无法还原二叉树的。如果在二叉树的三种遍历序列中给出其中的两种，是否可以唯一确定一棵二叉树呢？
由先序和中序遍历序列还原二叉树：由二叉树的先序与中序序列可以唯一确定一棵二叉树。因为，二叉树的先序遍历先访问根结点 D，其次遍历左子树 L，然后遍历右子树 R。即在先序遍历序列中，第一个结点必为根结点；而在中序遍历时，先遍历左子树 L，然后访问根结点 D，最后遍历右子树 R，因此中序遍历序列被根结点分为两部分：根结点之前的部分为左子树结点中序序列，根结点之后的为右子树结点中序序列。通过这两部分再到先序序列中找到左右子树的根结点，如此类推，便可唯一得到一棵二叉树。
　　如：已知一棵二叉树的先序序列为 EBADCFHG，其中序序列为 ABCDEFGH。图 6-14说明了还原二叉树的过程。

 

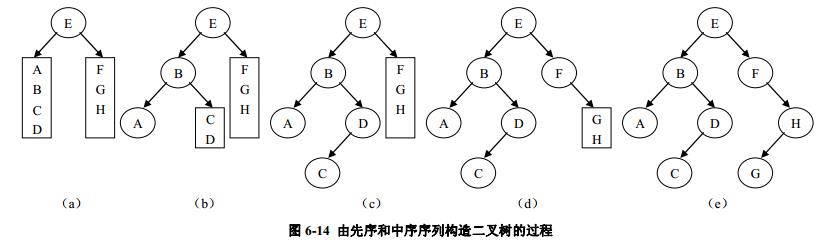
　　首先由先序序列知道二叉树的根结点为 E，则其左子树的中序序列为（ ABCD），右子树的中序序列为（ FGH）。反过来知道二叉树左子树的先序序列为（ BADC），右子树先序序列为（ FHG）。然后对二叉树的左右子树分别用先序和中序序列分析其根结点及其左右子树，直到得到整个二叉树结构。由后序和中序遍历序列还原二叉树：同样，同过二叉树的后序和中序序列也可以唯一确定一棵二叉树。其方法与上述方法类似，只不过此时根结点是出现在后序序列的最后面。由先序和后序序列不能唯一确定一棵二叉树。例如：先序序列为 AB，后序序列为 BA。此时就无法确定二叉树的结构，因为 B 既可以是根 A 的左子树，也可以是根的右子树。