机器学习基石：04 Feasibility of Learning

Posted 2020-10-09

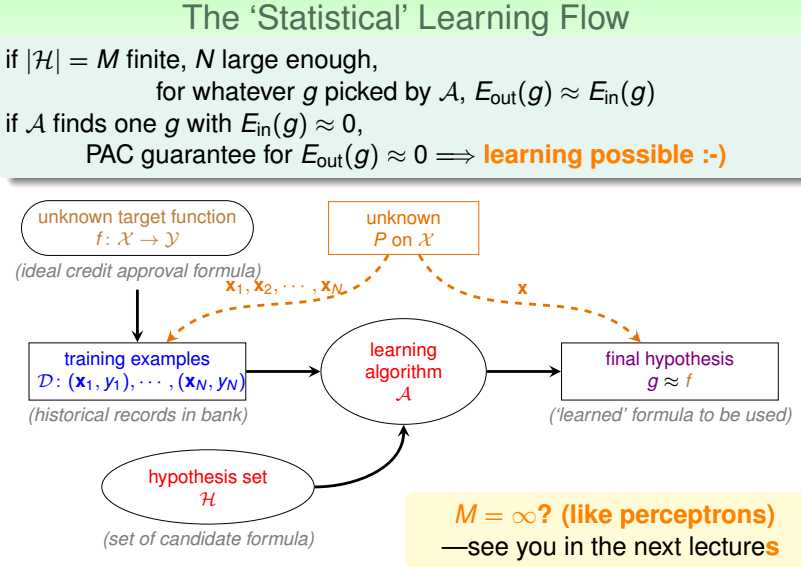
机器学习是设计算法A，在假设集合H里，根据给定数据集D，选出与实际模式f最为相近的假设g（g可能与f相同，也可能不同）。

那什么情况下学习是可行的？即保证g和f是相似的。

1.数据集内的表现g约等于f;

2.g在数据集外的表现约等于g在数据集内的表现。

结合1,2可保证，由算法在给定数据集上学习到的g（即数据集内的表现g约等于f）在数据集外的表现也约等于f。即g与f相似。

 

如何保证2？

数据集内表现相同的多个假设在数据集外的部分数据上表现相差极大，即学习效果极差。

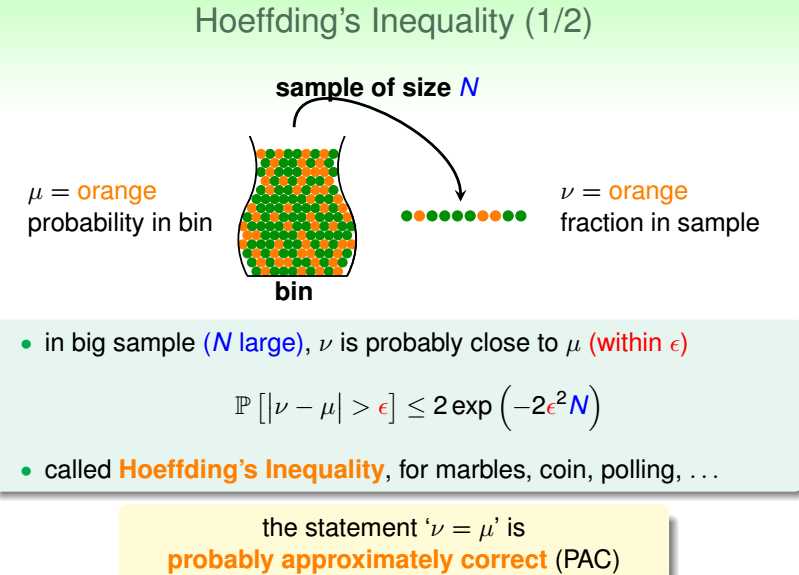
霍夫丁不等式，

有一个装有绿色小球和橘色小球的罐子（假设球数无限），从中进行N次有放回的取球实验，在这N次实验中取出橘色小球的频率为v，

只要N足够大，就可以用v来估计mu即罐子中橘色小球的实际概率。

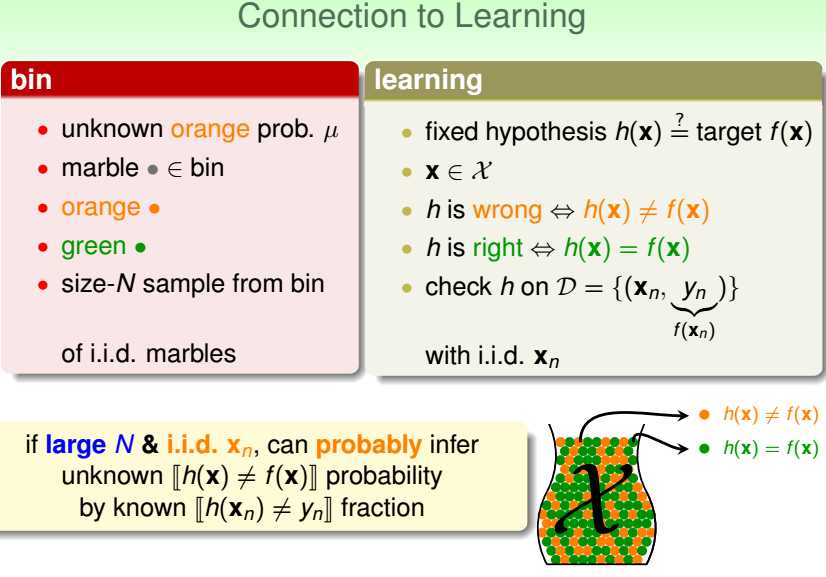
与学习相联系，

当h选定时，只要D里样本数N足够大且样本点独立同分布，

就能保证h在整个输入空间里的表现（异常点的概率）与数据集内的表现（D里异常点的频率）在一定的概率范围内近似相等。

注意，E_out(h)实际是面向整个输入空间的，即数据集D内+数据集D外。

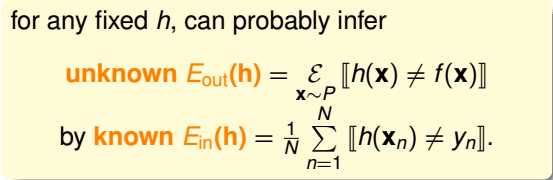
如何保证1？

A根据D在H中选出使得E_in(h)小的h。

注意，2的保证是在给定h的情况下，即h的选择只有1个。

但是，1的保证需要在H中进行选择，如果H的size>1，即h有很多个，可能有限，可能无限，那么2的保证是否受到影响？

坏数据：对于一个h，使得h在该数据内外表现差异很大的数据为坏数据。

可以理解为霍夫丁不等式的左式中概率衡量的事件：E_in(h)和E_out(h)的差异大于容忍度epsilon，

即对于一个h，存在坏数据的概率小于等于霍夫丁的右式。对于一个输入空间X，能够产生的用于训练的数据D有很多个，若对于一个h，给定的数据刚好就是坏数据的概率是小于等于霍夫丁的右式的。

若有M个h，给定的数据是其中某个h的坏数据的概率是小于等于数据为h₁的坏数据的概率+数据为h₂的坏数据的概率+数据为h₃的坏数据的概率+......+数据为h_M的坏数据的概率。

本质是求并集（小于等于的原因是有可能存在交集）。

这里的M实际是|H|。

只要M是有限值，只要N足够大，不等式的右式就能足够小。

所以，只要假设集大小有限、N足够大------保证E_in和E_out的差异在容忍度内，

A根据D在H中挑选出g------保证E_in小，

就能说学习是PAC可能的。

但是，

如果输入空间X是无限的，那理论上对应的H的数量也是无限的，

那|H|无限时，怎么办？