HDU 5690 All X (快速幂）

Posted 2020-10-09 hinata_hajime

All X

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2469    Accepted Submission(s): 1022

Problem Description

F(x,m) 代表一个全是由数字x 组成的m 位数字。请计算，以下式子是否成立：

F(x,m) mod k ≡ c

 

 

Input

第一行一个整数T ，表示T 组数据。
每组测试数据占一行，包含四个数字x,m,k,c

1≤x≤9

1≤m≤10的10次方

0≤c<k≤10,000

 

 

Output

对于每组数据，输出两行：
第一行输出："Case #i:"。i 代表第i 组测试数据。
第二行输出“Yes” 或者 “No”，代表四个数字，是否能够满足题目中给的公式。

 

 

Sample Input

3 1 3 5 2 1 3 5 1 3 5 99 69

 

 

Sample Output

Case #1: No Case #2: Yes Case #3: Yes

Hint

对于第一组测试数据：111 mod 5 = 1，公式不成立，所以答案是”No”，而第二组测试数据中满足如上公式，所以答案是 “Yes”。

 

分析：由于题目中的m的范围很大，所以直接一步一步取模肯定是不行的，

但是我们可以观察到题目中这些数的特点就是每位的数字都一样，每位的数字都一样的话我们可以表示成

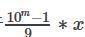这样的化就转化为了快速幂的问题

 

 

进一步转化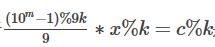

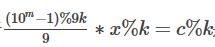
代码如下：

#include <map>
#include <stack>
#include <queue>
#include <cmath>
#include <vector>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
ll MOD;
ll mi(ll a,ll b)
{
ll   ans=1;
   a=a%MOD;
   while(b>0)
   {
    if(b&1)ans=(ans*a)%MOD;
    b=(b>>1);
    a=(a*a)%MOD;
   }
   return ans;
}
int main()
{
     ll t,x,m,k,c,r,Case=0;
     scanf("%lld",&t);
     while(t--)
     {
         Case++;
       scanf("%lld%lld%lld%lld",&x,&m,&k,&c);
       MOD=9*k;
       r=(mi(10,m)-1)/9*x%k;
       printf("Case #%lld:\\n",Case);
       if(r==c)puts("Yes");
       else puts("No");
     }
    return 0;
}

 

 

 

i