51nod 1296 有限制的排列（DP）

Posted 2020-10-08 Sakits

　　对于一个i，如果要比邻居大，那么i比i-1大，i+1比i小，比邻居小同理。设v[i]=0表示i与i-1的关系无限制，v[i]=1表示a[i-1]>a[i]，v[i]=2表示a[i-1]<a[i]

　　则有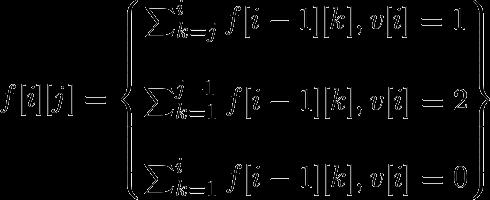

 　　显然这个是可以用前缀和优化成O(N^2)的

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define MOD(x) (x>=mod?x-mod:x)
using namespace std;
const int maxn=5010,mod=1e9+7;
int n,m1,m2,x,y;
int f[maxn][maxn],v[maxn];
void read(int &k)
{
    int f=1;k=0;char c=getchar();
    while(c<\'0\'||c>\'9\')c==\'-\'&&(f=-1),c=getchar();
    while(c<=\'9\'&&c>=\'0\')k=k*10+c-\'0\',c=getchar();
    k*=f;
}
int main()
{
    read(n);read(m1);read(m2);
    for(int i=1;i<=m1;i++)read(x),v[x+1]=1,v[x+2]=2;
    for(int i=1;i<=m2;i++)read(x),v[x+1]=2,v[x+2]=1;
    f[1][1]=1;
    for(int i=2;i<=n;i++)
    {
        if(v[i]==1||!v[i])for(int j=i,sum=0;j;j--)sum=MOD(sum+f[i-1][j]),f[i][j]+=sum;
        if(v[i]==2||!v[i])for(int j=1,sum=0;j<=i;j++)f[i][j]=MOD(f[i][j]+sum),sum=MOD(sum+f[i-1][j]);
    }
    int ans=0;
    for(int i=1;i<=n;i++)ans=MOD(ans+f[n][i]);
    printf("%d\\n",ans);
}

View Code