多项式曲线拟合
Posted 哈哈哈
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多项式曲线拟合相关的知识,希望对你有一定的参考价值。
给定数据点pi(xi,yi),其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y,i=1,2,...,m。
损失计算:
1.使偏差绝对值之和最小
![]()
2.使偏差绝对值最大的最小
3.使偏差平方和最小
![]()
推导:
拟合多项式: 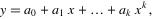
计算误差: 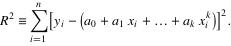
求参数,求偏导:
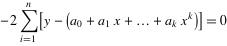
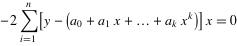
。。。。
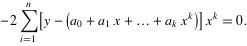
得到:
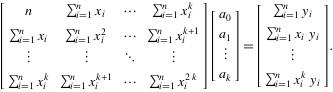
#include <cv.h> #include <highgui.h> using namespace std; bool polynomialCurveFit(vector<cv::Point> & training, int n, cv::Mat& A) { int N = training.size(); cv::Mat x = cv::Mat::zeros(n + 1, n + 1, CV_64FC1); for (int i = 0; i < n + 1; i++) { for (int j = 0; j < n + 1; j++) { for (int k = 0; k < N; k++) { x.at<double>(i, j) = x.at<double>(i, j) + pow(training[k].x, i + j); } } } cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1); for (int i = 0; i < n + 1; i++) { for (int k = 0; k < N; k++) { Y.at<double>(i, 0) = Y.at<double>(i, 0) + pow(training[k].x, i)*training[k].y; } } A = cv::Mat::zeros(n + 1, 1, CV_64FC1); cv::solve(x, Y, A, cv::DECOMP_LU);
//solve 是OpenCV中专用于求解线性方程的函数。。 x左矩阵,y右矩阵,A系数矩阵, method 估算方法。。 参数少于点数,LU分解 return true; } int main() { cv::Mat image = cv::Mat::zeros(480, 640, CV_8UC3); image.setTo(cv::Scalar(0, 0, 0)); vector<cv::Point> points; points.push_back(cv::Point(100., 58.)); points.push_back(cv::Point(150., 70.)); points.push_back(cv::Point(200., 90.)); points.push_back(cv::Point(252., 140.)); points.push_back(cv::Point(300., 220.)); points.push_back(cv::Point(350., 400.)); for (int i = 0; i < points.size(); i++) cv::circle(image, points[i], 5, cv::Scalar(0, 0, 255), 2, 8, 0); cv::polylines(image, points, false, cv::Scalar(0, 255, 0), 1, 8, 0); cv::Mat A; polynomialCurveFit(points, 3, A); cout << A << endl; vector<cv::Point>points_fitted; for (int x = 0; x < 400; x++) { double y = A.at<double>(0, 0) + A.at<double>(1, 0)*x + A.at<double>(2, 0)*pow(x, 2) + A.at<double>(3, 0)*pow(x, 3); points_fitted.push_back(cv::Point(x, y)); } cv::polylines(image, points_fitted, false, cv::Scalar(0, 255, 255), 1, 8, 0); cv::imshow("image", image); cv::waitKey(0); return 0; }
拟合结果
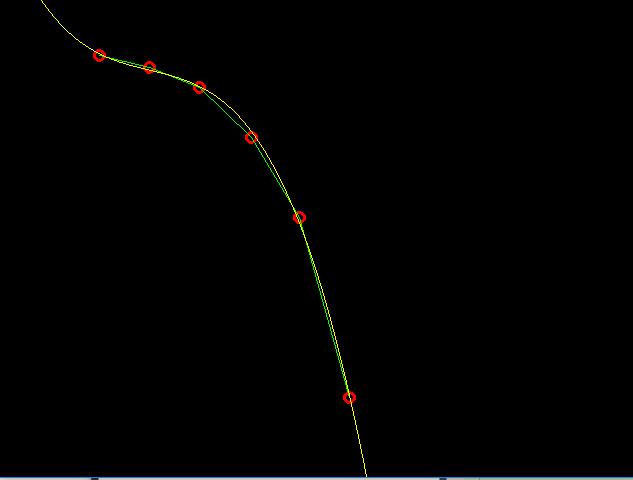
以上是关于多项式曲线拟合的主要内容,如果未能解决你的问题,请参考以下文章
Apache Commons Math3学习笔记 - 多项式曲线拟合(转)