MATLAB点云处理（十六）：多项式曲线拟合（RANSAC | MSAC）

Posted 2021-08-30 没事就要敲代码

文章目录

• • 1 多项式拟合函数 fitPolynomialRANSAC
  • 2 代码实现

1 多项式拟合函数 fitPolynomialRANSAC

fitPolynomialRANSAC — 使用RANSAC算法从点云中进行多项式拟合

该函数使用M-估计量样本一致性（MSAC）算法，即随机样本一致性（RANSAC）算法的改进算法来拟合数据。

主要有 2 种重载方式

NO.1 给定数据点xyPoints、拟合阶数N、内点到模型的最大距离maxDistance，返回多项式系数P

P = fitPolynomialRANSAC(xyPoints,N,maxDistance)

通过对xyPoints中给定的 $m$ 个二维平面点进行多项式拟合，找到多项式系数P（按将幂排列）。

对于多项式 $p(x)=p_1{x}^n+p_2{x}^{n-1}+...+p_{n}x+p_{n+1}$，对应的多项式系数为 $P=[p_1,p_2,...,p_n,p_{n+1}]$

其中，

• xyPoints ：即[x y]， 为二维平面坐标点，为m×2阶矩阵
• N ：多项式拟合阶数，为大于 0 的整数
• maxDistance ：内点到模型的最大距离，为正数
• P：多项式系数，作为数值向量返回。每个元素对应于N次多项式方程中的一个系数数。例如，对于二次多项式，$A{x}^2+Bx+C=0$ 对应 $P[A,B,C]$

NO.2 给定数据点xyPoints、拟合阶数N、内点到模型的最大距离maxDistance，返回多项式系数P和内点的线性索引inlierIdx

[P,inlierIdx] = fitPolynomialRANSAC(xyPoints,N,maxDistance)

2 代码实现

示例1： 对空间种一组曲线点，投影到xoy平面进行RANSAC多项式拟合（直线拟合）

代码：

clc;
clear;

% 加载点云
ptCloud = pcread('line.pcd');

figure;
pcshow(ptCloud);
title('原始点云');
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');

% 提取xoy平面坐标点
x = ptCloud.Location(:,1);
y = ptCloud.Location(:,2);

figure;
plot(x,y,'.');
title('xoy平面投影点云');
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');

% 设置多项式拟合阶数 N
N = 1;

% 设置内点到模型的最大距离
maxDistance = 0.1;

% 执行MSAC多项式拟合
[P, inlierIdx] = fitPolynomialRANSAC([x,y],N,maxDistance);

% 输出多项式系数
P

% 使用polyval计算多项式，用红色圆圈标记异常值
x1 = linspace(min(x),max(x));	% 在区间[min.x,max.x]内生成100个等间距的x，用与计算多项式的值
yRecoveredCurve = polyval(p,x1);
figure;
plot(x1,yRecoveredCurve,'-g','LineWidth',2);
hold on;
plot(x(inlierIdx),y(inlierIdx),'.',x(~inlierIdx),y(~inlierIdx),'ro');
legend('多项式拟合曲线','内点','外点','Location','SouthEast');
title('拟合结果展示')
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');
hold off;

结果展示：

P =

  1×2 single 行向量

    0.6178    1.0817

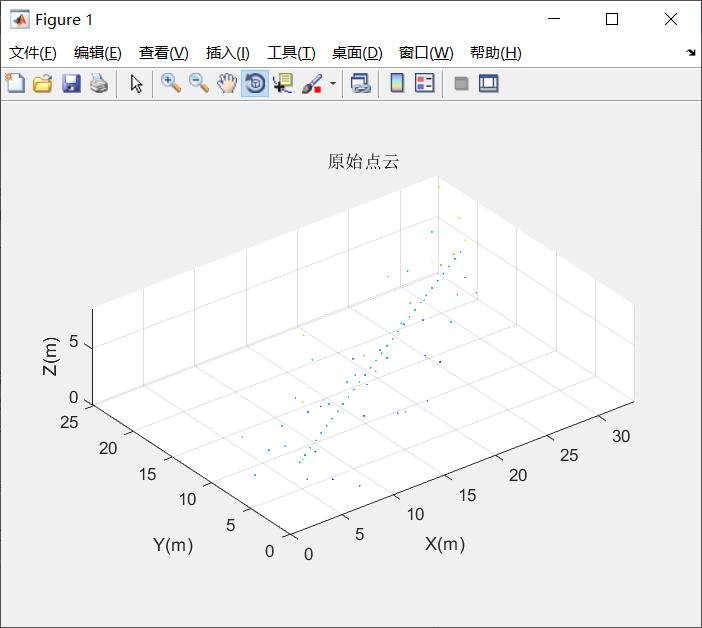
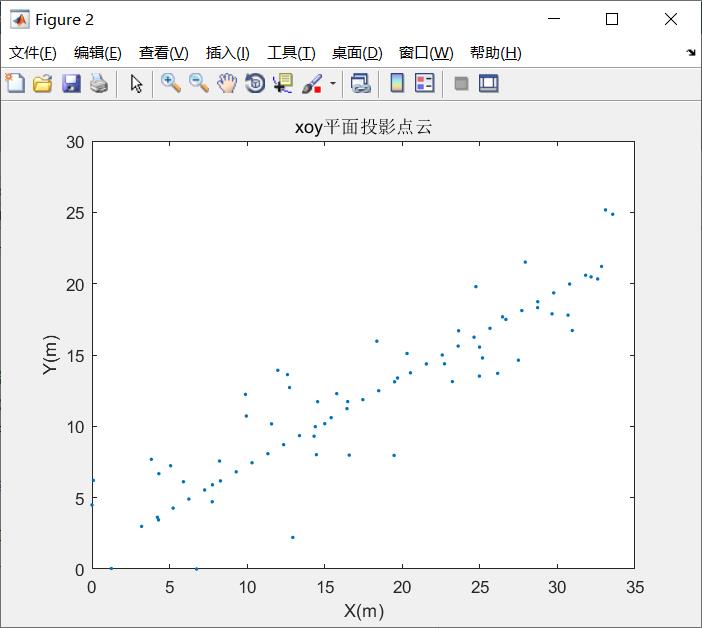
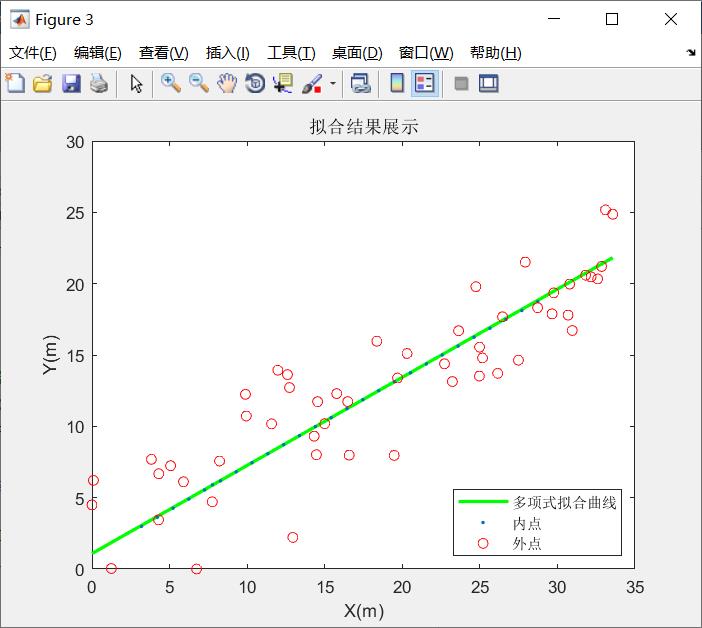
示例2： 对空间种一组曲线点，投影到xoy平面进行RANSAC多项式拟合（二次曲线拟合）

代码：

clc;
clear;

% 加载点云
 ptCloud = pcread('test2.pcd');

% 提取xoy平面坐标点
x = ptCloud.Location(:,1);
y = ptCloud.Location(:,2);

figure;
plot(x,y,'.');
title('xoy平面投影点云');
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');

% 设置多项式拟合阶数 N
N = 2;

% 设置内点到模型的最大距离
maxDistance = 0.1;

% 执行MSAC多项式拟合
[P, inlierIdx] = fitPolynomialRANSAC([x,y],N,maxDistance);

% 输出多项式系数
P

% 使用polyval计算多项式，用红色圆圈标记异常值。
x1 = linspace(min(x),max(x));	% 在区间[min.x,max.x]内生成100个等间距的x，用与计算多项式的值
yRecoveredCurve = polyval(P,x1);
figure;
plot(x1,yRecoveredCurve,'-g','LineWidth',2);
hold on;
plot(x(inlierIdx),y(inlierIdx),'.',x(~inlierIdx),y(~inlierIdx),'ro');
legend('多项式拟合曲线','内点','外点','Location','SouthEast');
title('拟合结果展示')
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');
hold off;

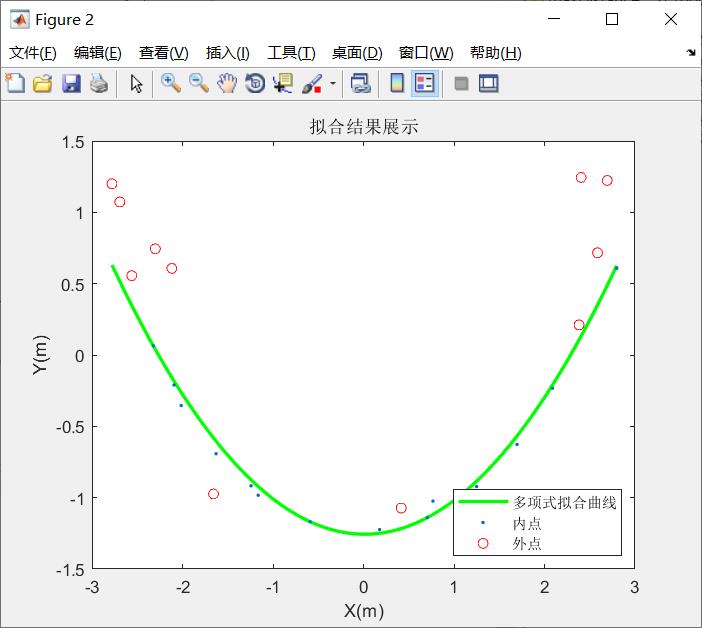
结果展示：

P =

  1×3 single 行向量

    0.2424   -0.0054   -1.2563

---

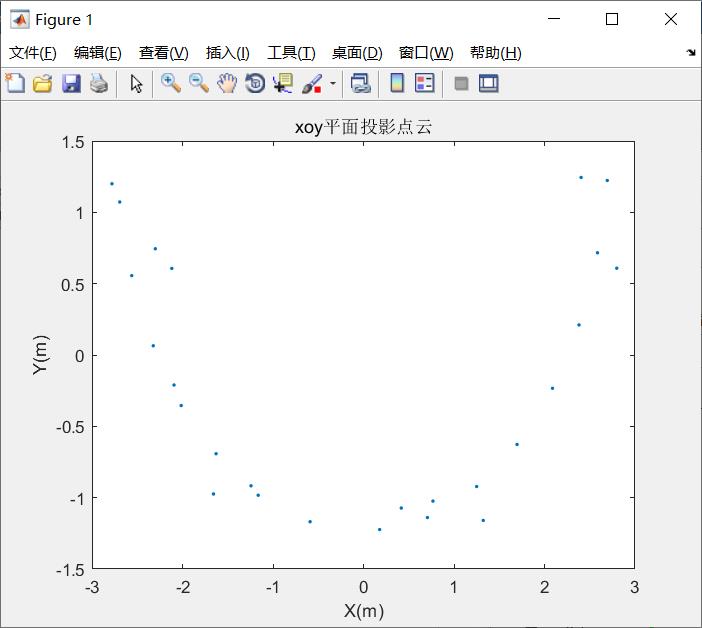
参考链接

https://ww2.mathworks.cn/help/vision/ref/fitpolynomialransac.html#bvhql22-2