PRML 1.1 多项式曲线拟合

Posted 2021-08-08 Real&Love

PRML 1.1 多项式曲线拟合

---

• 输入 训练集

  $$x\equiv (x_1,...,x_N{)}^T$$
  $$t\equiv (t_1,...,t_N{)}^T$$

• 输出 拟合曲线

1.1.1 代码

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1)
X = np.linspace(0, 1, 10)
y = np.sin(2*np.pi*X) + np.random.normal(0.1, 0.1, 10)  # 加入噪声
X_true = np.linspace(0, 1, 256, endpoint=True)
y_true = np.sin(2*np.pi*X_true)

plt.scatter(X, y, c="b", alpha=0.6)
plt.plot(X_true, y_true, c="g")
plt.show()

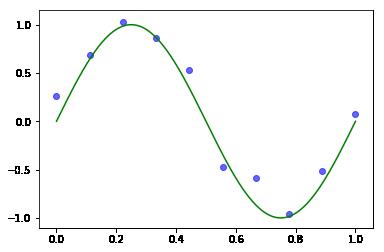
可以看到绿色的是潜在的待发现的函数$\sin (2\pi x)$，也就是我们最终想预测到对拟合曲线，但是现在根据输入【10个点的数据集】来进行拟合的。

1.1.2 多项式推导

我们需要用一个公式来拟合这些点，假设这是一个关于x的多项式

$$y(x,\omega )={\omega }_0+{\omega }_{1}x+{\omega }_2{x}^2+...+{\omega }_M{x}^M=\sum _{j=0}^M{\omega }_j{x}^j$$

• 上面公式中$M$表示多项式的阶数
• 当$M=1$时，为简单的线性回归方程

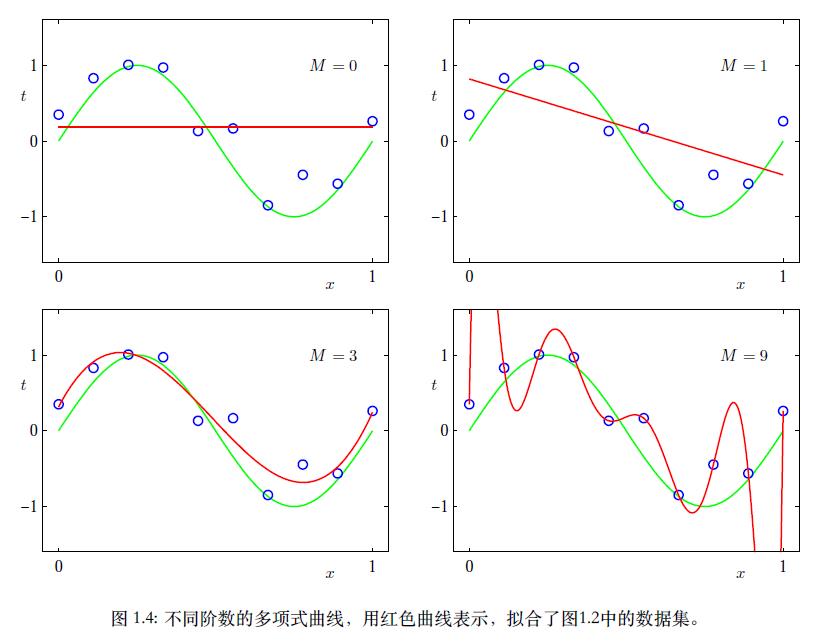
当𝑀=0M=0或𝑀=1M=1时，拟合曲线如下图上部分的红线所示

我们肉眼可以看到，拟合效果是非常差的。我们怎么量化这种训练时的误差呢？故引出下面常见的一种度量方法。
每个数据点的预测值$y(x_n,\omega )$和真实值$t_n$之间的平方和，这个$E(\omega )$很明显越小越好
$$E(\omega )=\frac{1}{2}\sum _{n=1}^N[y(x_n,\omega )-t_n{]}^2$$

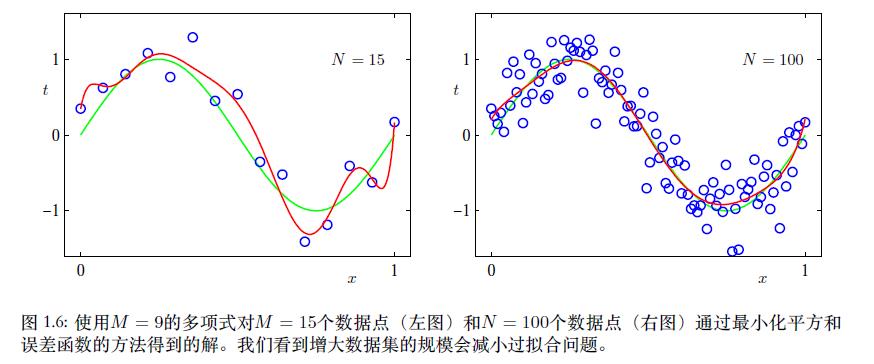
1.1.3 过拟合

解决过拟合的方法较多，如调节模型参数数量，让模型变得简单；加入正则项惩罚模型的复杂度，增加训练集的个数

1.1.4 正则化

我们给误差函数增加一个惩罚项。如下所示：
$$E(\omega )=\frac{1}{2}\sum _{n=1}^N[y(x_n,\omega )-t_n{]}^2+\frac{\lambda }{2}{\Vert \omega \Vert }^2$$

其中
$${\Vert \omega \Vert }^2={\omega }^T\omega ={\omega }_0^2+{\omega }_1^2+...+{\omega }_M^2$$

• 统计学 : 收缩法(shrinkage)【xgboost也会用到此方法】
• 神经网络: 权值衰减(weight decay)