深度解读最流行的优化算法：梯度下降（精简版）

Posted 2020-10-07

前言

本文仅对一些常见的优化方法进行直观介绍和简单的比较，各种优化方法的详细内容及公式只好去认真啃论文了，在此不赘述。

SGD

此处的SGD指mini-batch gradient descent，关于batch gradient descent, stochastic gradient descent, 以及 mini-batch gradient descent的具体区别就不细说了。现在的SGD一般都指mini-batch gradient descent。

SGD就是每一次迭代计算mini-batch的梯度，然后对参数进行更新，是最常见的优化方法了。即：

其中，是学习率，是梯度 SGD完全依赖于当前batch的梯度，所以可理解为允许当前batch的梯度多大程度影响参数更新

缺点：（正因为有这些缺点才让这么多大神发展出了后续的各种算法）

• 选择合适的learning rate比较困难 - 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征，有时我们可能想更新快一些对于不经常出现的特征，对于常出现的特征更新慢一些，这时候SGD就不太能满足要求了

• SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点【原来写的是“容易困于鞍点”，经查阅论文发现，其实在合适的初始化和step size的情况下，鞍点的影响并没这么大。感谢@冰橙的指正】

Momentum

momentum是模拟物理里动量的概念，积累之前的动量来替代真正的梯度。公式如下：

其中，是动量因子

特点：

• 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的能够进行很好的加速
• 下降中后期时，在局部最小值来回震荡的时候，，使得更新幅度增大，跳出陷阱
• 在梯度改变方向的时候，能够减少更新 总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛

Nesterov

nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度。 将上一节中的公式展开可得：

可以看出，并没有直接改变当前梯度，所以Nesterov的改进就是让之前的动量直接影响当前的动量。即：

所以，加上nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。如下图：

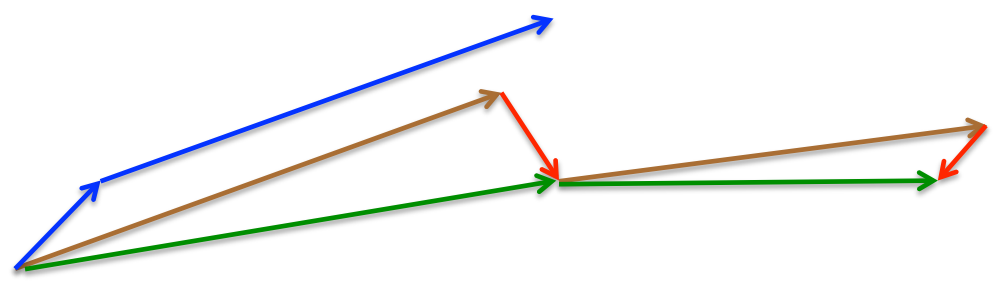
momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

其实，momentum项和nesterov项都是为了使梯度更新更加灵活，对不同情况有针对性。但是，人工设置一些学习率总还是有些生硬，接下来介绍几种自适应学习率的方法

Adagrad

Adagrad其实是对学习率进行了一个约束。即：

此处，对从1到进行一个递推形成一个约束项regularizer，，用来保证分母非0

特点：

• 前期较小的时候， regularizer较大，能够放大梯度
• 后期较大的时候，regularizer较小，能够约束梯度
• 适合处理稀疏梯度

缺点：

• 由公式可以看出，仍依赖于人工设置一个全局学习率
• 设置过大的话，会使regularizer过于敏感，对梯度的调节太大
• 中后期，分母上梯度平方的累加将会越来越大，使，使得训练提前结束

Adadelta

Adadelta是对Adagrad的扩展，最初方案依然是对学习率进行自适应约束，但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值。即：

在此处Adadelta其实还是依赖于全局学习率的，但是作者做了一定处理，经过近似牛顿迭代法之后：

其中，代表求期望。

此时，可以看出Adadelta已经不用依赖于全局学习率了。

特点：

• 训练初中期，加速效果不错，很快
• 训练后期，反复在局部最小值附近抖动

RMSprop

RMSprop可以算作Adadelta的一个特例：

当时，就变为了求梯度平方和的平均数。

如果再求根的话，就变成了RMS(均方根)：

此时，这个RMS就可以作为学习率的一个约束：

特点：

• 其实RMSprop依然依赖于全局学习率
• RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
• 适合处理非平稳目标 - 对于RNN效果很好

Adam

Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。公式如下：

其中，，分别是对梯度的一阶矩估计和二阶矩估计，可以看作对期望，的估计；，是对，的校正，这样可以近似为对期望的无偏估计。 可以看出，直接对梯度的矩估计对内存没有额外的要求，而且可以根据梯度进行动态调整，而对学习率形成一个动态约束，而且有明确的范围。

特点：

• 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
• 对内存需求较小
• 为不同的参数计算不同的自适应学习率
• 也适用于大多非凸优化 - 适用于大数据集和高维空间

Adamax

Adamax是Adam的一种变体，此方法对学习率的上限提供了一个更简单的范围。公式上的变化如下：

可以看出，Adamax学习率的边界范围更简单

Nadam

Nadam类似于带有Nesterov动量项的Adam。公式如下：

可以看出，Nadam对学习率有了更强的约束，同时对梯度的更新也有更直接的影响。一般而言，在想使用带动量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果。

经验之谈

• 对于稀疏数据，尽量使用学习率可自适应的优化方法，不用手动调节，而且最好采用默认值
• SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠
• 如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用学习率自适应的优化方法。
• Adadelta，RMSprop，Adam是比较相近的算法，在相似的情况下表现差不多。
• 在想使用带动量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果

最后展示两张可厉害的图，一切尽在图中啊，上面的都没啥用了... ...

图5：SGD optimization on loss surface contours

 

图6：SGD optimization on saddle point

 

转载：https://zhuanlan.zhihu.com/p/22252270?utm_source=qq&utm_medium=social