算法设计与分析基础22最优二叉查找树

Posted 2020-10-02 cutter_point

package cn.xf.algorithm.ch08DynamicProgramming;

import java.util.Arrays;

import org.junit.Test;

import cn.xf.algorithm.ch08DynamicProgramming.vo.ResultVo;

/**
 * 最优二叉树问题
 * 
 * 思路：根据最优二叉树的问题就是查找对应的节点的比较次数的期望值保持最小
 * 最优二叉查找树的期望搜索代价保持最小
 * 例如：一颗树有节点{k0,k1,k2,k3....kn} 对应搜索概率是:{p0,p1,p2....pn}
 * 那么根据二叉的深度设定对应的代价，那么就是
 * depth(ki) * pi + ..... 所有的都加起来，那么就是期望搜索代价
 * .
 * 
 * @版权：福富软件 版权所有 (c) 2017
 * @author xiaof
 * @version Revision 1.0.0
 * @see:
 * @创建日期：2017年8月9日
 * @功能说明：
 *
 */
public class BinaryTreeBest {
    
    /**
     * 对于这个概率求最优二叉查找树
     * 这里的关键是C[1，0] = 0  C[1，1] = Pi  前者作为空树存在，后者作为单节点树
     * @param probabilities
     */
    public ResultVo optimalBST(double probabilitiesT[]) {
        if(probabilitiesT == null || probabilitiesT.length <= 0) {
            return null;
        }
        
        //初始化，最优二叉查找树的期望搜索代价数组，以及主键最优二叉树的数组
        //数组后置一位，并把开头设置为空
        double probabilities[] = new double[probabilitiesT.length + 1]; 
        for(int i = 1; i < probabilities.length; ++i) {
            probabilities[i] = probabilitiesT[i - 1];
        }
        
        double C[][] = new double[probabilities.length + 1][probabilities.length + 1];
        int R[][] = new int[probabilities.length + 1][probabilities.length + 1];
        for(int i = 0; i < probabilities.length; ++i) {
            C[i][i] = probabilities[i]; //这个是单节点情况，
            R[i][i] = i;
        }
        
        //遍历所有的节点数量海数据,遵循公式 C[i,j] = (i->j)p + min{(i->k-1)depth(ki)pi + (k+1->j)depth(ki)pi }
        //根据对角线的差距数据获取值，因为递归求出的值得顺序是
        //C[1,2], C[2,3], C[3,4],C[4,5],C[5,6]....
        //C[1,3], C[2,4], C[3,5],C[4,6],C[5,7]....
        //C[1,4], C[2,5], C[3,6],C[4,7],C[5,8]....
        //这些数据以对角线的模式递增,数据之间的差距在慢慢变大，在C[1，N]之前的差额数据还是n-1，那么就是比如5个节点，就是4
        for(int d = 0; d < probabilitiesT.length; ++d) {
        	//这个是循环i与j的差距大小
        	//接下来循环开始位置，个数是实际的节点个数
        	for(int start = 1; start < probabilitiesT.length; ++start) {
        		//起始位置，然后根据当前差距，判定后面的位置j
        		int endj = start + d;
        		//超出当前循环最大长度
        		if(endj >= C[0].length - 1) {
        		    continue;
        		}
        		double min = Integer.MAX_VALUE; //设定当前最小值，作为一个起始判断对象
        		int kmin = start;
        		//设定中间划分点,只有两个不等，或者后面endj比start大的时候才可以进入递推队列
        		if(start != endj) {
        		    for(int midk = start; midk <= endj; ++midk) {
                        //判断当前分区的位置是否是最小的
                        if(midk + 1 < C.length && C[start][midk - 1] + C[midk + 1][endj] < min) {
                            //如果是这个选中的k的中间断点的最优二叉查找树
                            min = C[start][midk - 1] + C[midk + 1][endj];
                            kmin = midk;
                        }
                    }
        		    
        		    //统计start到endj的概率和
                    double sum = 0;
                    for(int i = start; i <= endj; ++i) {
                        sum += probabilities[i];
                    }
                    C[start][endj] = sum + min;
                    R[start][endj] = kmin;
        		}
        	}
        }
        ResultVo resultVo = new ResultVo();
        resultVo.setC(C);
        resultVo.setR(R);
        return resultVo;
    }
    
    @Test
    public void test1() {
    	double probabilities[] = {0.15, 0.10, 0.05, 0.10, 0.20};
//    	double probabilities[] = {0.1, 0.2, 0.4, 0.3};
    	BinaryTreeBest btb = new BinaryTreeBest();
    	ResultVo resultVo = btb.optimalBST(probabilities);
    	System.out.println();
    	//输出最优查找期望阵列
    	System.out.println("最优查找期望阵列");
    	double C[][] = resultVo.getC();
    	for(int i = 0; i < C.length; ++i) {
    	    for(int j = 0; j < C[0].length; ++j) {
    	        System.out.print(C[i][j] + "\\t");
    	    }
    	    System.out.println();
    	}
    	
    	//二叉树构建矩阵
    	System.out.println("二叉树构建矩阵");
    	int R[][] = resultVo.getR();
    	for(int i = 0; i < R.length; ++i) {
            for(int j = 0; j < R[0].length; ++j) {
                System.out.print(R[i][j] + "\\t");
            }
            System.out.println();
        }
    }
}

　　

截图：

 

 

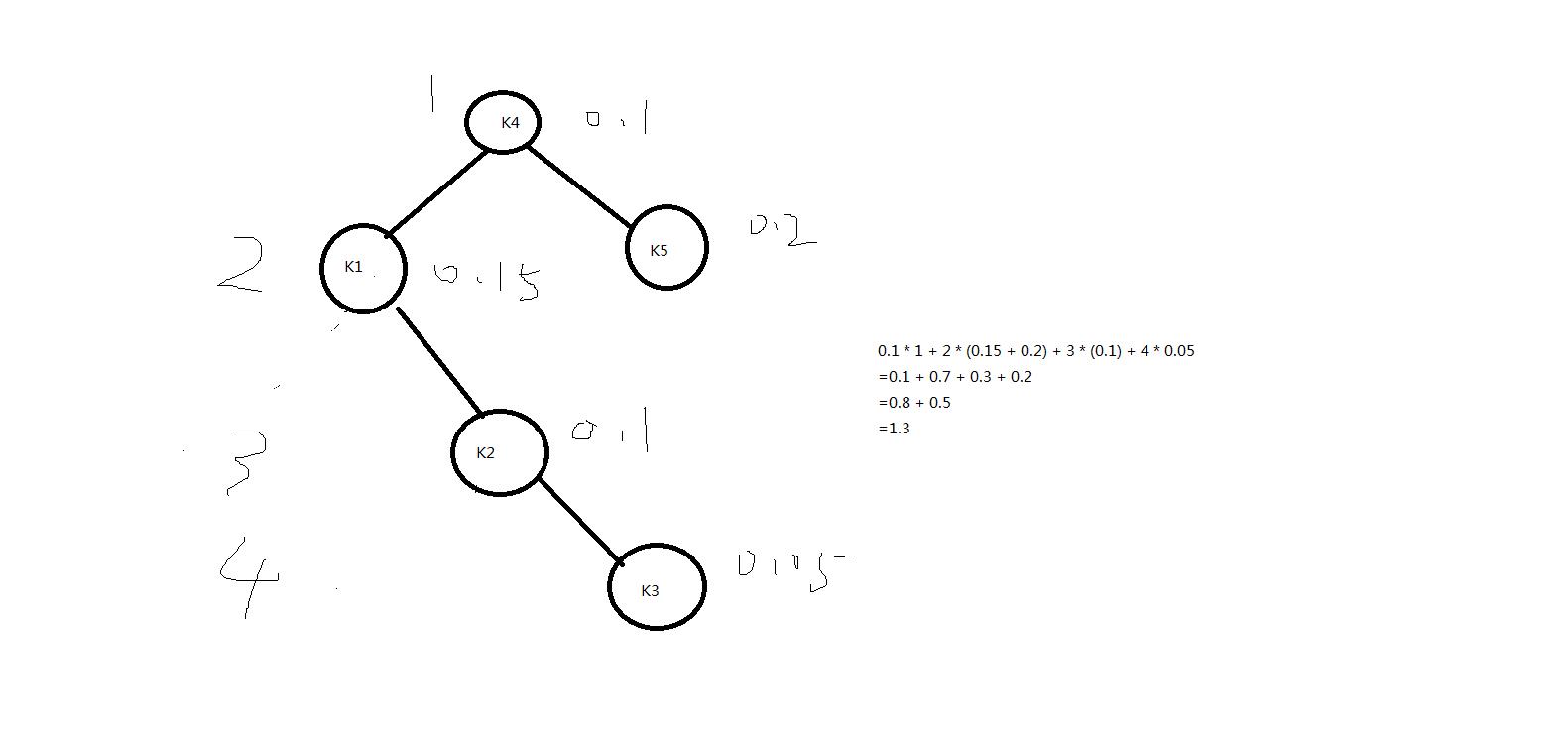
结果：