二叉搜索树和最优二叉搜索树的时间复杂度各是多少？

Posted 2023-03-29

最优二叉搜索树不是用了三重循环么？那样不应该是O（n的三次方）么？

二叉查找树（BST，Binary Search Tree） ，又名二叉搜索树或二叉检索树，是一颗满足如下条件的树：
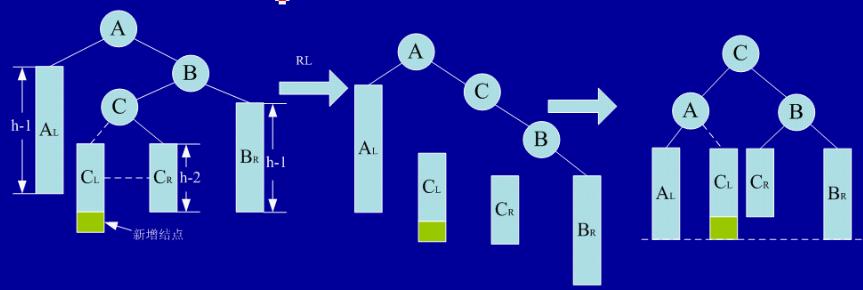
1、每个节点包含一个键值
2、每个节点有最多两个孩子
3、对于任意两个节点x和y，它们满足下述搜索性质:
a、如果y在x的左子树里，则key[y] <= key[x]
b、如果y在x的右子树里，则key[y] >= key[x]

最优二叉查找树（Optimal BST，Optimal Binary Search Tree）
最优二叉查找树是使查找各节点平均代价最低的二叉查找树。具体来说就是：给定键值序列 K = <k1 , k2 , . . . , kn >，k1 < k2 <· · · < kn ，其中键值ki ,被查找的概率为pi ，要求以这些键值构建一颗二叉查找树T，使得查找的期望代价最低（查找代价为检查的节点数）。
下面是对于查找期望代价的解释：
对于键值ki , 如果其在构造的二叉查找树里的深度（离开树根的分支数）为depthT(ki )，则搜索该键值的代价= depthT(ki ) +1（需要加上深度为0的树根节点）。由于每个键值被查找的概率分别为pi ，i=1,2,3…,n。所以查找期望代价为：
E[T的查找代价] = ∑i=1~n (depthT(ki ) +1) · pi
时间复杂度
1、穷举
穷举构造最优二叉查找树，其实就是这样的一个问题：
给一个拥有n个数的已排序的节点，可以将其构造成多少种不同的BST（用来找到一个最优的二叉查找树）？
设可以构造成T(n)个，那么枚举每一个元素作为根节点的情况，当第一个元素作为根节点时，其余n-1个构成右子树，无左子树，是n-1情况时的子问题， 共T(n-1)种；当第二个元素作为根节点时，左子树有1个元素，右子树有n-2个元素，根据乘法原理共有T(1)T(n-2)种情况……依此类推得 到：T(n) = T(0)T(n-1) + T(1)T(n-2) + T(2)T(n-3) + ...... + T(n-2)T(1) + T(n-1)T(0)；此外，有T(0)=T(1)=1。
下面来求解T(n)：
定义函数 f(x) = T(0) + T(1) · x + T(2) · x2 + ......
那么有：
f(x)2 = (T(0)2 ) + (T(0)T(1) + T(1)T(0)) · x + (T(0)T(2) + T(1)T(1) + T(2)T(0)) · x2 + ......
= T(1) + T(2) · x + T(3) · x2 + ......
= (f(x) - T(0)) / x
= (f(x) - 1) / x
这样解方程得到 f(x) = [1 - (1 - 4x)1/2 ] / 2x
右边进行泰勒展开，再与定义式比较最终得到： T(n) = (2n)! / (n!(n+1)!)
然后根据Stirling公式：n! ～ (2πn)1/2 · (n/e)n
于是有(2n)! / n!(n+1)! ～ (4n1/2 · 2n2n ) / (2n1/2 · nn · (2(n+1))1/2 · (n+1)n )
～ 4n · (n+1)-3/2 · (n/(n+1))n
～ 4n · n-3/2
因此最后得到穷举方法构造最优二叉查找树的时间复杂度： T(n) = O(4n · n-3/2 )

2、递归
实际上左右子树是互不影响的，不需要穷举所有左右子树的组合，所以不需要用乘法原理，加法原理就可以了，这样式子变为：
T(n) = T(0) + T(n-1) + T(1) + T(n-2) + T(2) + T(n-3) + ...... + T(n-2) + T(1) + T(n-1) + T(0)
= 2(T(0) + T(1) + T(2) + ...... + T(n-1))
= 3T(n-1)
所以得到T(n) = O(3n ) ，还是指数级的一个算法

3、动态规划
上面得到指数级算法的原因在于，计算了很多重复的子树情况，一些子树的查找代价被计算了很多遍；而一棵树如果是最优二叉搜索树，那么要么它是空树，要么它 的左、右子树也是最优二叉搜索树，因此只需要将子树的查找代价记录下来，采用记忆化搜索或者是自底向上的动态规划的方法，虽然需要消耗一定的空间，但可以 把时间复杂度从指数级降到多项式级，这些空间消耗也是可以接受的。
以下是采用自底向上的解法：
输入：键值序列 K = <k1 , k2 , . . . , kn >，概率序列 P = <p1 , p2 , . . . , pn >
输出：两个二维数组，Price[i][j]表示ki 到kj 构成的最优子树的查找代价，Root[i][j]表示表示ki 到kj 构成的最优子树的根节点位置（用于重构最优二叉查找树）
算法1 ：
For 子树大小size = 1 to n
For 子树的起点start = 1 to (n - size + 1) //这样子树的终点即为 end = start + size - 1，长度为size
For 该子树的所有节点作为根节点root = start to end
对于每个root，根据之前计算过的Price数组得到左右最优子树的代价，可直接得到该子树的代价price为：
左右子树的最优子树代价之和 + 所有节点的访问概率之和（因为所有节点都下降了一层）
在内层循环中找到代价最小的price和root分别记录在Price[start][end]和Root[start][end]中

下面分析这个算法的时间复杂度：
由于除了计算出我们最后需要得到的Price和Root二维数组，还产生了部分冗余的子树，因此不能简单的将算法归结为O(n2 )的算法。
对于子树大小为1时，我们考察了n个子树；
对于子树大小为2时，一共产生了(n - 1)个最优子树，但是在我们的每次考察中，都将子树的所有节点作为根节点考虑过一次，因此每得到1个大小为2的子树，我们需要考察2个不同的子树来找到一 个代价最小的，因此最后我们实际上考察了2(n - 1)个子树；
对于子树大小为3时，类似的，我们考察了3(n - 2)个子树；
……
对于子树大小为n时，我们考察了n个子树。
最后，我们一共考察了T(n) = n + 2(n - 1) + 3(n - 2) + ...... + n个子树。
求解这个公式依然可以借用之前的方法，定义函数 f(x) = 1 + 2x + 3x2 + ...... = (1 - x)-2
这样一来 f(x)2 = T(1) + T(2) · x + T(3) · x2 + ......
再借用泰勒展开得到 T(n) = (n + 2)(n + 1)n/6 = O(n3 )
或者把所有项视为n2，则有 T(n) ≤ n2 + n2 + n2 + n2 + ...... = (n+1)n2 ≤ 2n3
把中间n/2项都视为n/4 · 3n/4的话，则有 T(n) ≥ n/2 · n/4 · 3n/4 = (3/32)n3
根据时间复杂度的定义有 T(n) = O(n3 )

下面介绍一个定理，可以借此把动态规划算法的时间复杂度进一步降到O(n2 )，详细的证明参见参考文献：
定理1 ：Root[i][j-1] ≤ Root[i][j] ≤ Root[i+1][j] （Root数组定义见算法1）

也就是说，算法1的第3个For就可以不用循环子树中的所有节点了，只要循环另两个子树的根节点之间的范围就可以了。算法如下，红色的为修改的部分：
算法2 ：
For 子树大小size = 1 to n
For 子树的起点start = 1 to (n - size + 1) //这样子树的终点即为 end = start + size - 1，长度为size
For 该子树的所有节点作为根节点root = Root[start][end-1] to Root[start+1][end]
对于每个root，根据之前计算过的Price数组得到左右最优子树的代价，可直接得到该子树的代价price为：
左右子树的最优子树代价之和 + 所有节点的访问概率之和（因为所有节点都下降了一层）
在内层循环中找到代价最小的price和root分别记录在Price[start][end]和Root[start][end]中
在分析该算法的时间复杂度时应注意，考察的子树是与考察的内层循环中root数量一一对应的，而当start递进时，前一个root的终点正好等于后一个root的起点（算法中的红色部分），也就是说对于固定的size来说，考察的root的范围加起来应当首位相接 而且至多刚好覆盖 所有节点，因此对于每个size，最多只考察2n个root（这里缩放了一下），因此总共最多考察了2n · n = 2n2 个子树；另一方面，Root数组中每一个值对应得到的一个最优二叉查找树，也即至少需要考察n2 个子树。因此根据定义得到 T(n) = O(n2 ) 参考技术A 二叉搜索树
最好：以2为底n的对数
最坏：n
最优二叉搜索树
最好/最坏：以2为底n的对数本回答被提问者采纳

动态规划习题之最优二叉搜索树

题目

问题描述：
        给定一个n元素的中序序列，它可以有卡特兰数个不同形状的二叉排序树。（卡特兰数的定义及证明参见组合数学）：

，如果我们知道每个键的查找概率，怎么来构造一个平均查找代价最小（查找成功）的最优二叉查找树呢？
-----------------------------------------------------------------------------------------------------------
      用动态规划来求解，首先要找到它的最优子结构性质，然后根据这个最优子结构来描述和刻画问题，得到状态转移的方程：
1）最优子结构性质：
        看看一颗最优二叉查找树是怎么得到的？逆向思维，如果现在有一棵最优二叉查找树，root是ak，很容易得出：ak的左右子树也是最优二叉查找树（如果它的子树不是最优的，那就说明这个子树还可以继续调整，那么ak那颗树就也不是最优的了）。

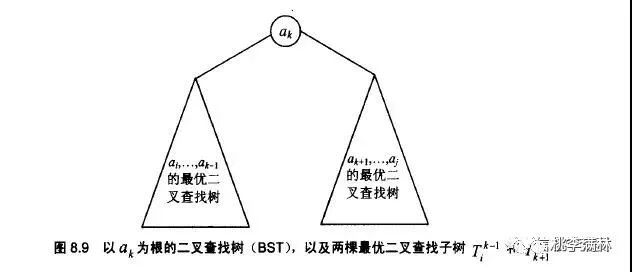
2）根据最优子结构性质来描述和刻画问题
        用C[i , j]表示从 i 到 j 的最优二叉查找树的代价，那么问题就被划分为了n^2个子问题了（顶点号从0计数），假设有n个顶点，那么我们的目标是要求C[0 , n-1]。（编号从0还是1开始无所谓，在编程的时候注意下标范围就行了）。
      现在根据它的最优子结构来找状态转移方程：从 i 到 j的一个最优二叉查找树是怎么得到的？（即一个C[i , j]是怎么来的），它是从 i 到 j 之间的顶点中选出一个顶点来做root，假设选出的这个做root的顶点是 k （i <= k <= j ）,那么显然有：

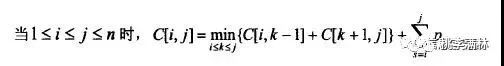
        这个式子其实可以直接想到，不用那么复杂的推导，它就是要找一个能使得C[i , j]代价最小的 k （这个k的范围在 i 到 j之间），而后面为什么要加一个从i到j的概率呢？因为挑出了k后，它作root，每个点的查找长度都增加了1。当然，也有更严格
的推导，可以参考下：

3）有了状态转移方程，就可以画个矩阵看看初始条件，以及每个C[i , j]依赖那些值（填表顺序）。
初始条件有：C[i , i] = Pi，C[i , i-1] = 0
试探一下一个C[i , j]是怎么来的，就可以看出，应该沿对角线来填。

注意状态转移方程里当 k = i 或者 k = j 时，C[i , i - 1] 或者 C[j+1 , j]是没有定义的，在编程中只需要特殊处理下就行：对于这种没有定义的取0，其他的取矩阵中的值。

最后一点，至于具体的实现，tmd书上总喜欢画一个不是从0开始的表，有时候甚至还横坐标从0开始，纵坐标从1开始，虽说

是为了填矩阵的方便，但看起来很狗。我一般n规模的问题，就开n * n的矩阵，下表从0到n-1，对超出边界的做一些特殊处

理就行了，就像上面的C[i , i-1]。看看书上的表（理解意思，具体实现我开的矩阵不一样，下标控制不一样）：

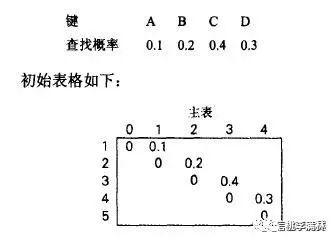
        它这样来画表其实就是为了解决C[i , i-1]不在定义范围内，为了能直接从矩阵中取值才这么做的。
-------------------------------------------------------------------------------------------------------------
        上面就构造出了最优二叉查找树的最优代价的动态规划过程，利用上述状态转移方程可以填出所有的C[i , j]。
        还有一个问题，怎么去不仅仅得到C[i , j]这个代价，更要知道对应于这个代价的二叉树的形状？
        仍然是构造一个矩阵 A[0...n-1，0...n-1] 来记录动态规划的过程，每次选出一个 k 作root时，就把 k 记录下来，即用A[i , j] = k 表示从 i 到 j 的最优二叉查找树的root是 k。（它还蕴含从 i 到 k - 1是左子树，k+1到 j 是右子树，注意我们给定的从0到n-1顶点是一个中序序列！）
    初始值 A[i , i] = i，表示只有自己的最优二叉查找树的root就是它自己。最后将得到一个矩阵A。它表达了二叉查找树的形状，当然，还得根据A的含义，从A中获取从 i 到 j的最优二叉查找树的形状。

        可以有下列算法，从A中输出从 i 到 j 的最优二叉查找树的形状（输出它的前序序列，因为中序序列是已知的）：

已知前序序列和中序序列，一个二叉树的形状就确定了：

也是用递归（最优子结构）
-------------------------------------------------------------------------------------------------------------
实现：

public class test {

/**

* @param args

*/

public static void main(String[] args) {

// TODO Auto-generated method stub

float[] P = {(float) 0.1,(float) 0.2,(float) 0.4,(float) 0.3};

//若返回值是最小代价，测试最小代价是否正确

//System.out.println("输出最优二叉排序树的最小代价： ");

//float result = OptBST(P);

//System.out.println(result);

//若返回值是表达最优二叉排序树形状的矩阵，测试矩阵是否正确

System.out.println("输出表达最优二叉排序树形状的矩阵： ");

int[][] R = OptBST(P);

for(int i = 0;i < R.length;i++)

{

for(int j = 0;j < R.length;j++)

System.out.print(R[i][j] + "　　");

System.out.println();

}

}

public static int[][] OptBST(float[] P){

//接受一个中序序列的点的查找概率数组，返回最优的二叉查找树的代价（注意P中的概率按顺序对应于点的中序序列）

int n = P.length; //结点个数

float[][] result = new float[n][n];

int[][] R = new int[n][n]; //表达二叉查找树形状的矩阵

for(int i = 0;i < n;i++)

{

result[i][i] = P[i]; //填充主对角线C[i,i] = P[i]

R[i][i] = i; //R[i][j]表示若只构造从i到j的树，那么root是R[i][j]

}

for(int d = 1;d <= n - 1;d++) //共n-1条对角线需要填充

{

for(int i = 0;i <= n - d - 1;i++) //横坐标的范围与对角线编号d的关系

{

int j = i + d; //一旦横坐标确定后，纵坐标可以用横坐标与对角线编号表示出来

float min = 1000000;

int root = 0;

for(int k = i;k <= j;k++)

{

float C1 = 0,C2 = 0; //用C1，C2表示result[i,k-1]和result[k+1,j]

if(k > i)

C1 = result[i][k - 1];

if(k < j)

C2 = result[k + 1][j];

if(C1 + C2 < min)

{

min = C1 + C2;

root = k;

}

}

R[i][j] = root; //R[i][j]的值代表从i到j的最优二叉查找树的根

float sum = 0;

for(int s = i;s <= j;s++)

//sum = sum + P[i]; 

sum = sum + P[s];

result[i][j] = sum + min;

}

}

//return result[0][n-1]; //返回C[1,n],最小代价

return R; //返回表达最优二叉排序树形状的矩阵

}

}

最优代价的矩阵和表达形状的矩阵在一起求的，需要哪个就返回哪个值，见代码。

很容易看出时间复杂度是 n^3（k的选择需要一个循环） 的，空间复杂度是 n^2的。

运行结果（返回表达二叉查找树形状的矩阵R）：

输出表达最优二叉排序树形状的矩阵：

0　　1　　2　　2　　

0　　1　　2　　2　　

0　　0　　2　　2　　

0　　0　　0　　3