数据结构：树 || 最优二叉树(赫夫曼树)

Posted 2021-04-09 赵同学的代码时间

同一组数据可以表示为不唯一的树，今天讲解的最优二叉树，通过合理安排结点顺序，在实际使用中，可以将访问次数尽可能减少，从而提高了算法的效率。

在设计赫夫曼树之前，我们需要知道每个结点访问的频率，从而能够计算他们加权路径的长度，由于访问次数可以用路径长度表示，通过加权路径长度可以计算出加权平均值，加权平均值最小的树即是最优二叉树。

---

原理：设计使加权路径长度平均值最小的树

WPL=wk*lk

（权重*路径长度）

赫夫曼算法：

（1）给定n个权值w1:wn,构成n棵二叉树的集合F=T1：Tn，其中每棵二叉树Ti只有一个带权为wi的根结点，左右子树均为空。

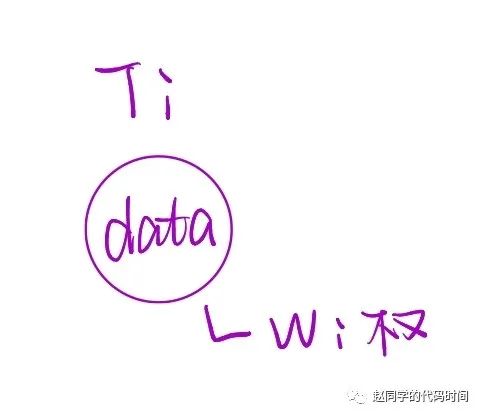
（2）从F中选权最小的两个作为左右子树构造一棵二叉树，把这棵树再加入到F中，w更新为原来两w之和，把原来两棵树弹出。
（3）重复（2）到只剩一棵树，便是赫夫曼树。

赫夫曼编码 || 赫夫曼树的应用

进行快速远距离传输时，为了提高传输速度，一种途径是，在保证不引起歧义的前提下，使得传输的字节数尽可能的少。赫夫曼树可以做到这一点，将赫夫曼树进行前缀编码，我们可以唯一的表示每个结点的位置。

下面看一个案例：

设8个字母为ABCDEFGH

字母	赫夫曼编码	二进制编码
E	0	100
G	10	110
B	110	001
H	1110	111
A	11110	000
D	111110	011
F	1111110	101
C	11111110	010

平均单个字符赫夫曼发送字数（加权平均数）

1×0.32+2×0.21+3×0.19+4×0.10+5×0.07+6×0.06+7×0.03+8×0.02=2.79

由于2.79<3

赫夫曼编码有着略微的优势

---

代码时间

Ⅰ存储结构，赫夫曼树和赫夫曼编码的存储表示

typedef struct{ unsigned int weight;//权重 unsigned int parent,lchild,rchild;//三格型二叉树}HTNode;//采用顺序存储结构parent用来存储是否有双亲（是否使用过）

//采用顺序存储结构parent用来存储是否有双亲（是否使用过）

Ⅱ建赫夫曼树

//假设已经给出或传入w[n]数组用于按顺序存放权重void createHuffmanTree(HTNode *&T, int *w, int n){ if (n <= 1) return; int m = 2 * n - 1; //按照顺序结构存储，我们需要多构建n-1个结点 HTNode *HT = (HTNode *)malloc((m + 1) * sizeof(sizeof(HTNode))); //弃用0号结点 HTNode *p = HT; int *m = w; int i; for (i = 1; i <= n; i++, p++, w++) *p = {*w, 0, 0, 0}; //初始化 for (; i < m; i++, p++) *p = {0, 0, 0, 0}; //继续初始化 for (i = n + 1; i <= m; i++) { //在1-（i-1）选择parent为0且weight和最小的两个结点，将他们贴到i结点上 int s1, s2, min = -1; for (int k = 1; k < i; k++) if (min > *(w + k)) { min = *(w + k); s1 = k; } //找最小 min = -1; for (int k = 1; k < i; k++) if (min > *(w + k) && k != s1) { min = *(w + k); s2 = k; }//找除s1最小 HT[s1].parent = i; HT[s2].parent = i; HT[i].lchild = s1; HT[i].rchild = s2; HT[i].weight = HT[s1].weight + HT[s2].weight; }}

Ⅲ 求赫夫曼编码（由叶子到根）

huffmancode *HC = (huffmancode*)malloc((n+1)*sizeof(char*));//指针空间char *cd = (char*)malloc(n*sizeof(char))//求编码工作空间//灵活使用数组等可以代替前两步cd[n-1]='';for(i=1;i<n;i++)//逐个字符求赫夫曼编码{ int start=n-1; for(int c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent){ if(HT[f].lchild==c) cd[--start]='0'; else cd[--start]='1'; } strcpy(HC[i],&cd[start]);//cd起到暂存作用，每一个编码都保存在字符串数组对应位置}free(cd);//释放空间