康托展开-全排列应用

Posted 2020-09-28 博客就叫Molex好了

我排第几个

时间限制：1000 ms  |  内存限制：65535 KB

难度：3

 

描述

现在有"abcdefghijkl”12个字符，将其所有的排列中按字典序排列，给出任意一种排列，说出这个排列在所有的排列中是第几小的？

 

输入

第一行有一个整数n（0<n<=10000）;
随后有n行，每行是一个排列；

输出

输出一个整数m，占一行，m表示排列是第几位；

样例输入

3
abcdefghijkl
hgebkflacdji
gfkedhjblcia

样例输出

1
302715242
260726926

普及一下数学知识

康托展开

　　康托展开的公式是 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中，ai为当前未出现的元素中是排在第几个（从0开始）。
　　这个公式可能看着让人头大，最好举个例子来说明一下。例如，有一个数组 s = ["A", "B", "C", "D"]，它的一个排列 s1 = ["D", "B", "A", "C"]，现在要把 s1 映射成 X。n 指的是数组的长度，也就是4，所以
X(s1) = a4*3! + a3*2! + a2*1! + a1*0!
关键问题是 a4、a3、a2 和 a1 等于啥？
a4 = "D" 这个元素在子数组 ["D", "B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，"D"是第3大的元素，所以 a4 = 3。
a3 = "B" 这个元素在子数组 ["B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，所以 a3 = 1。
a2 = "A" 这个元素在子数组 ["A", "C"] 中是第几大的元素。"A"是第0大的元素，"C"是第1大的元素，所以 a2 = 0。
a1 = "C" 这个元素在子数组 ["C"] 中是第几大的元素。"C" 是第0大的元素，所以 a1 = 0。（因为子数组只有1个元素，所以a1总是为0）
所以，X(s1) = 3*3! + 1*2! + 0*1! + 0*0! = 20

A B C | 0
A C B | 1
B A C | 2
B C A | 3
C A B | 4
C B A | 5

通过康托逆展开生成全排列

　　如果已知 s = ["A", "B", "C", "D"]，X(s1) = 20，能否推出 s1 = ["D", "B", "A", "C"] 呢？
　　因为已知 X(s1) = a4*3! + a3*2! + a2*1! + a1*0! = 20，所以问题变成由 20 能否唯一地映射出一组 a4、a3、a2、a1？如果不考虑 ai 的取值范围，有
3*3! + 1*2! + 0*1! + 0*0! = 20
2*3! + 4*2! + 0*1! + 0*0! = 20
1*3! + 7*2! + 0*1! + 0*0! = 20
0*3! + 10*2! + 0*1! + 0*0! = 20
0*3! + 0*2! + 20*1! + 0*0! = 20
等等。但是满足 0 <= ai <= n-1 的只有第一组。可以使用辗转相除的方法得到 ai，如下图所示：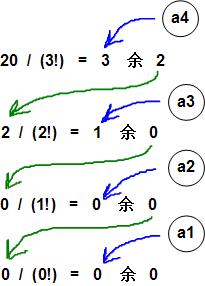

知道了a4、a3、a2、a1的值，就可以知道s1[0] 是子数组["A", "B", "C", "D"]中第3大的元素 "D"，s1[1] 是子数组 ["A", "B", "C"] 中第1大的元素"B"，s1[2] 是子数组 ["A", "C"] 中第0大的元素"A"，s[3] 是子数组 ["C"] 中第0大的元素"C"，所以s1 = ["D", "B", "A", "C"]。
这样我们就能写出一个函数 Permutation3()，它可以返回  s 的第 m 个排列。

前面的内容从http://archive.cnblogs.com/a/2026276/转载

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
long long fact[13];
char str[15];


int main()
{
    memset(fact,0,sizeof(fact));
    fact[0]=1;
    for(int i=1;i<=12;i++)
    {
        fact[i]=fact[i-1]*i;
    }
    int t;
    cin>>t;
    getchar();
    while(t--)
    {
        gets(str);
        long long sum=0;
        int len=strlen(str);
        for(int i=0; str[i]; i++)
        {
            int cnt=0;
            for(int j=i+1; str[j]; j++)
            {
                if(str[i]>str[j])
                {
                    cnt++;
                }
            }
            sum+=cnt*fact[len-1-i];
        }
        cout<<sum+1<<endl;
    }
    return 0;
}