NOI2015程序自动分析

Posted 2020-09-26 ssttkkl

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若?e=0，则该约束条件为xi≠xj；

 

输出格式：

 输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

 

输入输出样例

输入样例#1：

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例#1：

NO
YES

说明

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

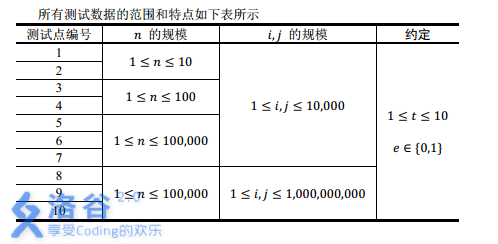
【时限2s，内存512M】

题解

并查集+离散化。

先执行所有x=y问题，合并x和y。

再依次执行所有x!=y问题，即查询x和y是否处于同一集合。如果是，则有x=y且x!=y，不满足条件。

如果所有的x!=y都得到满足，这组数据就可以满足。

注意到i,j范围为[1,1e9]，parent数组开不了这么大的范围。又注意到n范围只有[1,1e5]，考虑离散化。

先读入所有出现的数字，存到一个数组，然后排序并去重。之后操作用到的数字都在这个数组进行二分查找。

时间复杂度O(nlogn)。

注意的坑：

1、最多有n个操作，每个操作有两个数字，所以并查集的大小应该是n*2。

2、我写的时候二分查找返回的位置是从0开始的，并查集又写成从1开始，就WA了一个点，调了好久才发现问题。

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#define maxn 100005 * 2
using namespace std;
typedef unsigned long long ullint;
namespace djs
{
int parent[maxn];
inline void init()
{
    for (int i = 0; i < maxn; i++)
        parent[i] = -1;
}
inline int find(int x)
{
    int ance = x;
    while (parent[ance] >= 0)
        ance = parent[ance];

    int at = x;
    while (parent[at] >= 0)
    {
        int fa = parent[at];
        parent[at] = ance;
        at = fa;
    }

    return ance;
}
inline void merge(int x, int y)
{
    x = find(x);
    y = find(y);
    if (x == y)
        return;
    else
    {
        //令x为rank更大的，即parent值更小的
        if (parent[x] > parent[y])
            swap(x, y);
        parent[x] += parent[y];
        parent[y] = x;
    }
}
inline bool is_related(int x, int y)
{
    return find(x) == find(y);
}
}
typedef pair<ullint, ullint> query;
vector<query> q, m;                  //暂存查询、合并操作
vector<ullint> data;                 //存储读入的所有数据
vector<ullint>::iterator unique_end; //去重后的数据的尾后迭代器
inline int get_pos(ullint v)         //二分查找v在data所处的位置
{
    return lower_bound(data.begin(), unique_end, v) - data.begin();
}
int main()
{
    ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while (t--)
    {
        using namespace djs;

        int n;
        cin >> n;
        init();
        m.clear();
        q.clear();
        data.clear();

        ullint a, b, c;
        for (int i = 0; i < n; i++)
        {
            cin >> a >> b >> c;
            data.push_back(a);
            data.push_back(b);
            switch (c)
            {
            case 1:
                m.push_back(make_pair(a, b));
                break;

            case 0:
                q.push_back(make_pair(a, b));
                break;
            }
        }

        //离散化
        sort(data.begin(), data.end());
        unique_end = unique(data.begin(), data.end());

        //合并
        for (int i = 0; i < m.size(); i++)
            merge(get_pos(m[i].first), get_pos(m[i].second));

        //查询
        bool yes = true;
        for (int i = 0; i < q.size(); i++)
        {
            if (is_related(get_pos(q[i].first), get_pos(q[i].second)))
            {
                yes = false;
                break;
            }
        }
        if (yes)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}