一个行矩阵乘以一个列矩阵（一样大小）有啥物理或者几何意义?

Posted 2023-05-05

参考技术A 如果将行矩阵看成行向量(a1,a2,...,an)
列矩阵看成列向量(b1,b2,...,bn)T,其中T表示转置
行向量左乘列向量：(a1,a2,...,an)(b1,b2,...,bn)T=a1*b1+a2*b2+...+an*bn
其实就是这两个向量的内积（或称数量积）,其物理意义就是力对物体所做的功,几何意义就是一个向量在另一向量方向上的投影.
不废话了,感兴趣可以参考以下材料（从百度搜了几个帖子,自己看吧）：
物理百度吧中关于内积的一系列讨论：
百度文库中关于内积的PPT：
内积的一个提问：

理解矩阵乘法

线性代数中的矩阵乘法

矩阵加法就是相同位置的数字加一下。

矩阵减法也类似。

矩阵乘以一个常数，就是所有位置都乘以这个数。

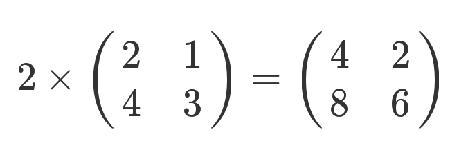
但是，等到矩阵乘以矩阵的时候，一切就不一样了。

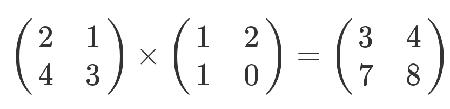
这个结果是怎么算出来的？

教科书告诉你，计算规则是，第一个矩阵第一行的每个数字（2和1），各自乘以第二个矩阵第一列对应位置的数字（1和1），然后将乘积相加（ 2 x 1 + 1 x 1），得到结果矩阵左上角的那个值3。

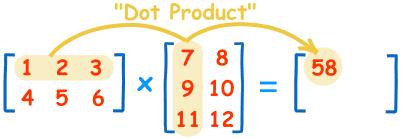
也就是说，结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。

怎么会有这么奇怪的规则？

线性代数是向量计算的基础，很多重要的数学模型都要用到向量计算。

矩阵乘法到底是什么东西。关键就是一句话，矩阵的本质就是线性方程式，两者是一一对应关系。如果从线性方程式的角度，理解矩阵乘法就毫无难度。

下面是一组线性方程式。

矩阵的最初目的，只是为线性方程组提供一个简写形式。

老实说，从上面这种写法，已经能看出矩阵乘法的规则了：系数矩阵第一行的2和1，各自与 x 和 y 的乘积之和，等于3。不过，这不算严格的证明，只是线性方程式转为矩阵的书写规则。

下面才是严格的证明。有三组未知数 x、y 和 t，其中 x 和 y 的关系如下。

x 和 t 的关系如下。

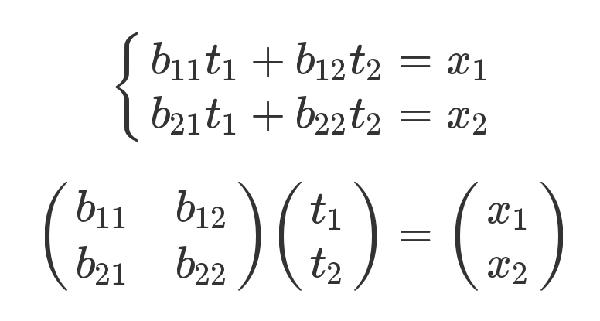
有了这两组方程式，就可以求 y 和 t 的关系。从矩阵来看，很显然，只要把第二个矩阵代入第一个矩阵即可。

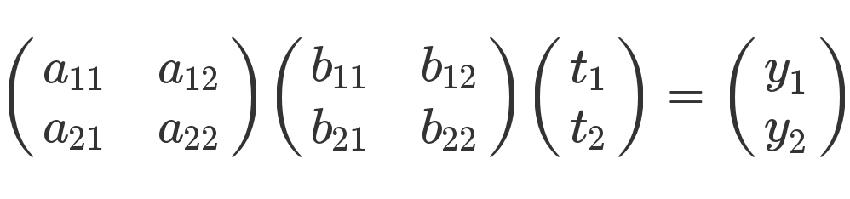
从方程式来看，也可以把第二个方程组代入第一个方程组。

上面的方程组可以整理成下面的形式。

最后那个矩阵等式，与前面的矩阵等式一对照，就会得到下面的关系。

矩阵乘法的计算规则，从而得到证明。