贝塞尔曲线
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贝塞尔曲线相关的知识,希望对你有一定的参考价值。
我想学习贝塞尔曲线,急需资料下载
我要方程
贝塞尔曲线是应用于二维图形应用程序的数学曲线。曲线的定义有四个点:起始点、终止点(也称锚点)以及两个相互分离的中间点。滑动两个中间点,贝塞尔曲线的形状会发生变化。二十世纪六十年代晚期,Pierre Bézier应用数学方法为雷诺公司的汽车制造业描绘出了贝塞尔曲线。
Pierre Bezier照片【命名】
贝塞尔曲线就是这样的一条曲线,它是依据四个位置任意的点坐标绘制出的一条光滑曲线。在历史上,研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。贝塞尔曲线的有趣之处更在于它的“皮筋效应”~也就是说,随着点有规律地移动,曲线将产生皮筋伸引一样的变换,带来视觉上的冲击。1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名~是为贝塞尔曲线。
[编辑本段]【作用】
由于用计算机画图大部分时间是操作鼠标来掌握线条的路径,与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形,拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作,所以到目前为止人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。
贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点(起始点、终止点以及两个相互分离的中间点)来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的,中间与贝塞尔曲线交叉,两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率(弯曲的程度);移动中间点(也就是移动虚拟的控制线)时,贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意,贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。
[编辑本段]【发现者】
“贝赛尔曲线”是由法国数学家Pierre Bézier所发现,由此为计算机矢量图形学奠定了基础。它的主要意义在于无论是直线或曲线都能在数学上予以描述。
[编辑本段]【贝赛尔工具】
“贝赛尔”工具在photoshop中叫“钢笔工具”;在CorelDraw中翻译成“贝赛尔工具”;而在Fireworks中叫“画笔”。它是用来“画线”造型的一种专业工具。当然还有很多工具也可以完成画线的工作,例如大家常用的photoshop里的直线、喷枪、画笔工具,Fireworks里的直线、铅笔和笔刷工具,CorelDraw里的自由笔,手绘工具等等。
用“贝塞尔”工具无论是画直线或是曲线,都非常简单,随手可得。其操作特点是通过用鼠标在面板上放置各个锚点,根据锚点的路径和描绘的先后顺序,产生直线或者是曲线的效果。我们都知道路径由一个或多个直线段或曲线段组成。锚点标记路径段的端点。在曲线段上,每个选中的锚点显示一条或两条方向线,方向线以方向点结束。方向线和方向点的位置确定曲线段的大小和形状。移动这些元素将改变路径中曲线的形状,可以看右图。路径可以是闭合的,没有起点或终点(如圆圈),也可以是开放的,有明显的端点(如波浪线)。
[编辑本段]【CorelDRAW贝塞尔曲线的使用方法】
贝塞尔曲线跟PS里的钢笔的意思大概差不多,不过贝塞尔曲线没有选取的功能。在这里,要切记,不要和轮廓工具弄混,前者是通过调节点调节形状,后者是调节形状轮廓的粗细以及样式。
补充几点:
1、在任意工具情况下,在曲线上双击都可以换为形状工具对曲线进行编辑;
2、在曲线上用形状工具双击可以增加一个节点;
3、在曲线的节点上双击形状工具可以删除一个节点;
4、位图可以用形状工具点击再拖动某一点可以进行任意形状的编辑;
5、用形状工具同时选中几个节点可以进行移动;
6、在微调距离中设定一个数值再用形状工具选中曲线的某一节点敲方向箭头可以进行精确位移;
7、将某一个汉字或字母转换为曲线就可以用形状工具进行修理如将“下”的右边的点拿掉等。
百度百科中的词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。 本词条对我有帮助
82
Android UI贝塞尔曲线 ① ( 一阶贝塞尔曲线 | 二阶贝塞尔曲线 )
文章目录
贝塞尔曲线参考 : https://github.com/venshine/BezierMaker
一、一阶贝塞尔曲线
一阶贝塞尔曲线 本质 是一条直线 , 下图是 一阶贝塞尔曲线 , P 0 P_0 P0 是曲线开始位置 , 逐个点向 P 1 P_1 P1 绘制 ;

二、二阶贝塞尔曲线
二阶贝塞尔曲线 需要在 一阶贝塞尔曲线 基础上 , 添加一个控制点 , 曲线的绘制受控制点影响 ;
下图中 由 P 0 P_0 P0 向 P 2 P_2 P2 绘制 二阶贝塞尔曲线 , 控制点是 P 1 P_1 P1 ;
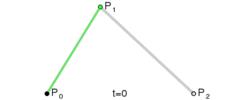
由 P 0 P_0 P0 点绘制一条曲线到 P 2 P_2 P2 点 , 绘制该曲线时 , 有一个控制点 P 0 P_0 P0 , 相当于 将曲线向 " 控制点 P 0 P_0 P0 " 方向拖动 , 产生一条圆滑的弧线 ;
上述绘制的 弧线 , 是通过计算得来的 , 绘制 P 0 P_0 P0 到 P 2 P_2 P2 的弧线 , 中间引入一个控制点 P 1 P_1 P1 ,

-
首先由 起始点 P 0 P_0 P0 与 控制点 P 1 P_1 P1 进行连线 ,
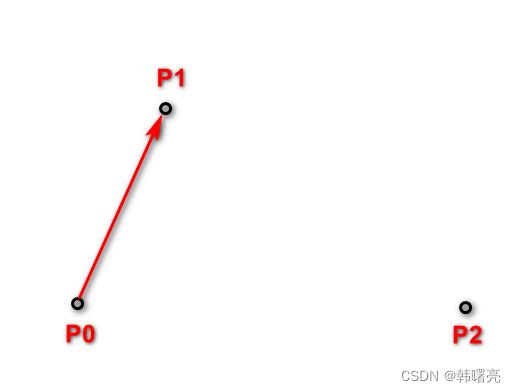
-
然后由 控制点 P 1 P_1 P1 与 结束点 P 2 P_2 P2 进行连线 ,

- P 0 P_0 P0 到 P 1 P_1 P1 可以认为是 一阶贝塞尔曲线 , P 1 P_1 P1 到 P 2 P_2 P2 也可以认为是 一阶贝塞尔曲线 ,
- 由 起始点 P 0 P_0 P0 与 控制点 P 1 P_1 P1 连线的这条线开始进行控制 ,
- 在 起始点 P 0 P_0 P0 与 控制点 P 1 P_1 P1 连线上找到一个 比例值 x x x ( 取值范围 0 − 1.0 0 - 1.0 0−1.0 ) , 找到 x x x 比例所处的点 A A A , 同时在 控制点 P 1 P_1 P1 与 结束点 P 2 P_2 P2 连线上 , 找到一个 比例值 x x x 对应的点 B B B , 将 A B AB AB 两个点进行连线 ,
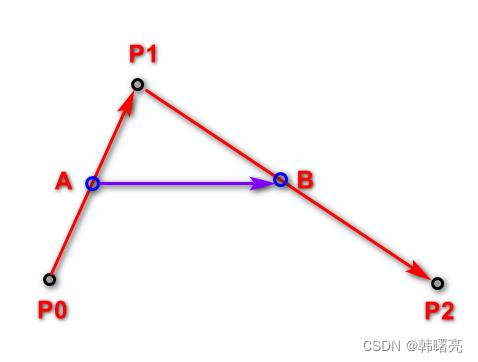
- 贝塞尔曲线上绘制的点 , 是 在 A B AB AB 连线上的 x x x 比例所在位置 , 绿色的点 C C C 就是贝塞尔曲线要绘制的位置 ;

上述计算过程中的比例 :
P 0 A P 0 P 1 = P 1 B P 1 P 2 = A C A B \\cfracP_0 AP_0 P_1 = \\cfracP_1 BP_1 P_2 = \\cfracACAB P0P1P0A=P1P2P1B=ABAC
其中 P 0 A P_0 A P0A 表示 P 0 P_0 P0 点到 A A A 点的线段长度 , P 0 P 1 P_0 P_1 P0P1 表示 P 0 P_0 P0 点到 P 1 P_1 P1 点的线段长度 ;
以上是关于贝塞尔曲线的主要内容,如果未能解决你的问题,请参考以下文章