数理统计基础 02 - 统计量和三大分布

Posted 2020-09-19 万物皆数

1. 样本和统计量

1.1 样本和统计量

　　数理统计讨论的问题不一定都是随机现象，比如人口信息的统计、具体数据的测量，它们的结果都是确定的。但实际问题的操作并不是数学所关心的，剥离问题的外壳，这些问题都可以用随机现象来描述，比如人口信息和测量误差都可以用一个正态分布来近似。建立统计的概率模型，正是数理统计区别于广义统计学的关键，为模型定义统一、明确的对象也是任何数学分支的起点。

　　既然这样，数理统计的研究对象其实还是随机变量，具体问题中所有可能的取值被称为全体，而每一个值称为个体。不同于概率论中研究分布的性质，统计中的分布信息往往是未知的，这样的随机变量习惯写作\\(X\\)。为了得到\\(X\\)的更多信息，需要采集它的观察值\\(X_1,X_2,\\cdots,X_n\\)，它们称为样本。一般假定\\(X_i\\)是与\\(X\\)同分布的独立随机变量，具体样本值则记作\\(x_i\\)。

　　统计问题中的主要信息就是样本值\\(X_i\\)，能对它进行的处理只有函数计算\\(f(X_1,\\cdots,X_n)\\)，这些函数值被称为样本统计量。统计量不能任意选取，它需要根据实际需要并一般有直观意义。比如最常用的统计量是式（1）中的样本均值\\(\\bar{X}\\)和样本方差\\(S^2\\)，它们一般作为分布的均值和方差的估计值。

\\[\\bar{X}=\\frac{1}{n}\\sum\\limits_{i=1}^nX_i;\\;\\;S^2=\\frac{1}{n-1}\\sum\\limits_{i=1}^n(X_i-\\bar{X})^2\\tag{1}\\]

　　既然样本是随机变量，统计量自然也是随机变量。如果\\(X\\)的期望和方差是\\((\\mu,\\sigma^2)\\)，则易知\\(\\bar{X}\\)是有期望\\(\\mu\\)和方差\\(\\dfrac{\\sigma^2}{n}\\)的随机变量。不难算得，\\(S^2\\)的期望值正好是\\(\\sigma^2\\)，所有系数取\\(\\frac{1}{n-1}\\)是合理的，\\(S^2\\)的完整称谓是“修正的样本方差”。我们暂时可以这样“直觉”地解释这个现象：均值\\(\\bar{X}\\)是由\\(X_i\\)生成的，它会随着\\(X_i\\)的变动而变动，这就导致真正自由、有效的变量减少了一个。下面马上会回来重新讨论这个问题。

　　更一般的，比较重要的统计量还有样本原点矩和样本中心距（式（2）），要注意\\(k>1\\)时，样本中心距都需要修正，只不过在\\(n\\)很大时可以近似地使用。其中一阶原点矩便是样本均值，二阶中心距便是未修正的样本方差，其它的统计量使用频率不高。

\\[a_k=\\frac{1}{n}\\sum\\limits_{i=1}^nX_i^k;\\;\\;m_k=\\frac{1}{n}\\sum\\limits_{i=1}^n(X_i-\\bar{X})^k\\tag{2}\\]

　　研究统计量是为了获取分布的信息，我们有一个很朴素的想法：当样本数足够多后，应当能绘制出分布函数\\(F(x)\\)的图形。根据分布函数的定义特点，可以定义这样一个统计量\\(v_n(x)\\)：它表示满足\\(X_i\\leqslant x\\)的样本数，并记\\(F_n(x)=\\dfrac{v_n(x)}{n}\\)，它称为经验分布函数。对于指定的\\(x\\)，\\(F_n(x)\\)是随机变量，当把\\(x\\)也看作变量时，我们只好叫\\(F_n(x)\\)“随机函数”。不过不用担心概念会变复杂，因为\\(|F_n(x)-F(x)|\\)的最大值才是我们要关心的，而它是一个随机变量。数理统计中有著名的格里文科定理（式（3）），它说明\\(F_n(x)\\)以概率\\(1\\)收敛于\\(F(x)\\)。

\\[P\\left\\{\\lim_{n\\to\\infty}\\sup_{x\\in\\mathbb{R}}\\left|F_n(x)-F(x)\\right|=0\\right\\}=1\\tag{3}\\]

1.2 统计量的自由度

　　在概率论中我们熟知一个结论：如果\\(X_1,\\cdots,X_n\\)互相不相关，则\\(Y=X_1+\\cdots+X_n\\)的期望、方差可以简单地展开。\\(n\\)个\\(X_i\\)对\\(Y\\)的影响互不相关，这样的统计量十分易于讨论，我们暂且称它的自由度是\\(n\\)。下面就来研究一下样本方差的自由度为什么是\\(n-1\\)而不是\\(n\\)，不过在此之前，需要先讨论一下随机变量正交变换的性质。

　　对互不相关的随机变量\\(X_i\\)，设对它们做正交线性变换后得到\\(Y_i\\)，则首先容易得到式（4）。然后分别展开\\(E(Y_iY_j)\\)和\\(E(Y_i)E(Y_j)\\)，根据正交性，以及\\(X_i\\)独立同分布，容易有式（5）成立，所以\\(Y_i\\)互不相关。这个结论对任何随机变量都成立，且也符合正交变换的一贯性质。

\\[(X_1,\\cdots,X_n)=(Y_1,\\cdots,Y_n)A;\\,AA^T=I\\;\\Rightarrow\\;\\sum_{i=1}^nX_i^2=\\sum_{i=1}^nY_i^2\\tag{4}\\]

\\[E(Y_iY_j)-E(Y_i)E(Y_j)=\\sum_{k=1}^na_{ki}a_{kj}(E(X_k^2)-E^2(X_k))=0\\tag{5}\\]

　　特别地，式（6）左的\\(Y_1\\)可以扩展为一个正交变换，利用式（4）便可得到式（6）右的结论。这不仅说明了\\(S^2\\)的自由度为\\(n-1\\)，还可以知道\\(\\bar{X}\\)和\\(S^2\\)是不相关的，这个结论非常重要。

\\[Y_1=\\sqrt{n}\\bar{X}\\;\\Rightarrow\\;\\sum_{i=1}^n(X_i-\\bar{X})^2=\\sum_{i=1}^nX_i^2-Y_1^2=\\sum_{i=2}^nY_i^2\\tag{6}\\]

　　对于满足再生性的随机变量，\\(Y_i\\)和\\(X_i\\)具有相同的分布类型，且可知满足式（6）的\\(Y_1\\)有期望\\(\\sqrt{n}\\mu\\)和方差\\(\\sigma^2\\)，而其它\\(Y_i\\)有期望\\(0\\)和方差\\(\\sigma^2\\)。特别地，当\\(X_i\\)是正态分布时，可以有式（7）成立，且\\(\\bar{X}\\)与\\(S^2\\)相互独立。对\\(\\bar{X}\\)的结论，一般写作式（8），右边是一个确定的分布（后面会用到）。

\\[X_i\\sim N(\\mu,\\sigma^2)\\;\\Rightarrow\\;Y_1\\sim N(\\sqrt{n}\\mu,\\sigma^2);\\; Y_i\\sim N(0,\\sigma^2)\\tag{7}\\]

\\[\\dfrac{\\sqrt{n}(\\bar{X}-\\mu)}{\\sigma}\\sim N(0,1)\\tag{8}\\]

　　更一般地，对于自由度为\\(n\\)的随机变量\\(Q=X_1^2+\\cdots+X_n^2\\)，其中\\(X_i\\)互不相关。现在把\\(Q\\)看成\\(X_i\\)的正定二次型，并记行向量\\(\\vec{X}=[X_1,\\cdots,X_n]\\)。假设\\(Q\\)可以分解为\\(r\\)个半正定二次型之和（式（9）左），且\\(Q_k\\)的秩\\(n_k\\)满足\\(n_1+\\cdots+n_r=n\\)。由\\(A_k\\)的秩为\\(n_k\\)且半正定可知，存在\\(n\\times n_k\\)的矩阵\\(B_k\\)，使得\\(Q_k=\\vec{X}B_kB_k^T\\vec{X}^T\\)。

\\[Q=Q_1+\\cdots+Q_r=\\vec{X}BB^T\\vec{X}^T=\\vec{Y}\\vec{Y}^T\\tag{9}\\]

　　令方阵\\(B=[B_1,\\cdots,B_r]\\)和\\(\\vec{Y}=\\vec{X}B\\)，则有\\(Q=\\vec{Y}\\vec{Y}^T\\)（式（9）右），从而\\(BB^T=I_n\\)，\\(B\\)是一个正交矩阵。因为\\(Y_j\\)是由\\(X_i\\)正交变换而来，故根据式（5）知\\(Y_j\\)互不相关，继而\\(Q_k\\)之间是互不相关的。值得提醒的是，当\\(Q\\)也是一般的半正定二次型时，结论仍然成立，这个条件使用起来会更方便，请自行论证。

　　现在利用这个结论再讨论\\(S^2\\)的自由度，首先显然有式（10）成立，其中的每一项都是关于\\(X_i\\)的半正定二次型。当半正定二次型具有形式\\(\\sum\\limits_{i=1}^nZ_i^2\\)，且\\(Z_i\\)还有\\(r\\)个线性约束条件时，它本质上是关于\\(n-r\\)个自由变量的正定二次型，从而秩为\\(n-r\\)。这个小结论在判定二次型秩时很有用，比如\\(S^2\\)中设\\(Z_i=X_i-\\bar{X}\\)，则有\\(1\\)个限制条件\\(Z_1+\\cdots+Z_n=0\\)，从而\\(S^2\\)的秩为\\(n-1\\)。另外显然式（10）左的秩为\\(n\\)，\\(\\bar{X}\\)的秩为\\(1\\)，满足以上定理的条件，故有\\(S^2,\\bar{X}\\)不相关。

\\[\\sum_{i=1}^nX_i^2=n\\bar{X}^2+(n-1)S^2\\tag{10}\\]

2. 统计学三大分布

　　统计量也是随机变量，各种形式的统计量会产生许多新的随机变量，这些变量中的有些是经常出现的，有必要事先对它们做一些介绍。因为正态分布适用的场合最为广泛，这里的统计学三大分布都是基于正态分布的。

2.1 \\(\\chi^2\\)（卡方）分布

　　在介绍\\(\\chi^2\\)分布之前，先讨论一个更一般的分布。将埃尔朗分布中的\\(r\\)扩展为任意正实数，得到的分布（11）称为\\(\\varGamma\\)分布，一般记作\\(\\varGamma(r,\\lambda)\\)。式子中的\\(\\varGamma(r)\\)确保了\\(p(x)\\)为密度函数，它被称为\\(\\varGamma\\)函数。\\(\\varGamma\\)函数在实数域是个\\(U\\)形函数，它有式（12）的基本结论，由于\\(\\varGamma(n)=(n-1)!\\)，它也被看成是阶乘概念的扩展。

\\[p(x)=\\dfrac{\\lambda^r}{\\varGamma(r)}x^{r-1}e^{-\\lambda x},\\;\\varGamma(x)=\\int_{-\\infty}^{+\\infty}t^{x-1}e^{-t}\\,\\text{d}t\\tag{11}\\]

\\[\\varGamma(x+1)=x\\varGamma(x);\\;\\;\\varGamma(1)=1,\\;\\varGamma(\\dfrac{1}{2})=\\sqrt{\\pi}\\tag{12}\\]

　　\\(\\varGamma\\)分布具有和埃尔朗分布同样的特征函数，并且也满足再生性。这里不打算讨论\\(\\varGamma\\)分布的更多性质，而是关注它的一类特例。假设\\(X\\sim N(0,1)\\)，可以证明\\(X^2\\sim\\varGamma(\\dfrac{1}{2},\\dfrac{1}{2})\\)，这是个奇妙的巧合！如果\\(X_1,\\cdots,X_n\\)是独立的标准状态分布，利用再生性有式（13）成立，它被称为自由度为\\(n\\)的\\(\\chi^2\\)（卡方）分布，记作\\(\\chi_n^2\\)。

\\[X_i\\sim N(0,1)\\;\\Rightarrow\\;\\sum_{i=1}^nX_i^2\\sim\\varGamma(\\dfrac{n}{2},\\dfrac{1}{2})=\\chi_n^2\\tag{13}\\]

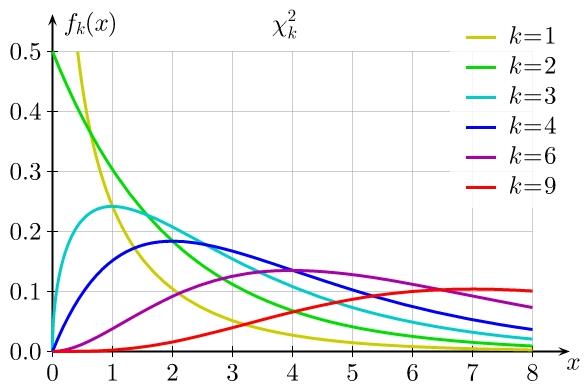
　　上图是\\(\\chi^2\\)分布的密度函数，\\(n=1\\)时便是\\(X^2\\)，它有两条渐近线，\\(n=2\\)时是指数分布，\\(n>2\\)时分布曲线类似但越来越扁平。容易算得\\(\\chi_1^2\\)有期望\\(1\\)和方差\\(2\\)，这就得到\\(\\chi_n^2\\)分布的期望和方差（式（14））。继续上面对\\(S^2\\)的讨论，由于\\(Y_i\\sim N(0,\\sigma^2)\\)，可以得到\\(S^2\\)满足式（15）。另外如果\\(X\\)是指数函数，显然有\\(2\\lambda X\\sim\\chi_2^2\\)。

\\[Y\\sim \\chi_n^2\\;\\Rightarrow\\;E(Y)=n;\\;D(Y)=2n\\tag{14}\\]

\\[\\dfrac{(n-1)S^2}{\\sigma^2}\\sim\\chi_{n-1}^2\\tag{15}\\]

　　\\(\\chi^2\\)分布的引入无非是为了讨论样本方差的性质，这个分布中不含有任何未知的参数，这种确定的分布非常便于概率的量化计算。但在量化分析的表达式中，不应该含有未知的参数（样本值\\(X_i\\)、样本容量\\(n\\)等属于已知量），这样的表达式一般称为枢轴变量。简单说，枢轴变量由已知量组成，且形成一个确定的分布，这个以后会深入讨论。

　　一般教材上自由度的概念定义在随机变量\\(Q=X_1^2+\\cdots+X_n^2\\)上，其中\\(X_i\\)是独立的标准正交分布。如果\\(Q\\)可以分解为\\(k\\)个半正定二次型，且秩的和为\\(n\\)，则根据前面关于自由度的结论，变换矩阵\\(B\\)为正交矩阵，从而\\(Y_i\\)也是互相独立的正交分布。进而\\(Q_k\\)是自由度为\\(n_k\\)的卡方分布，且它们互相独立。这个结论称为柯赫伦（Cochran）分解定理，在数理统计中有着非常普遍的应用。

2.2 \\(t\\)分布

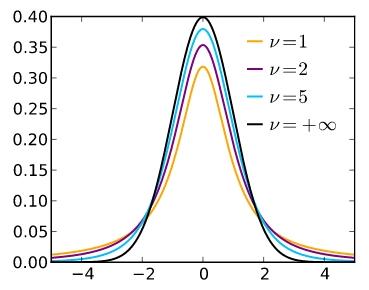
　　公式（8）中参数\\(\\sigma\\)往往是未知的，这会给分析带来困难，这时可以用\\(S\\)可以做为\\(\\sigma\\)的近似。令\\(X,Y\\)分别代表式（8）（15）中的变量，消除\\(\\sigma\\)后就形成变量\\(\\dfrac{X}{\\sqrt{Y/(n-1)}}\\)。这应当是我们要关心的数轴变量，它的分布是确定，为了便于讨论研究，需要为它作个定义。一般地，式（16）中的分布被称为自由度为\\(n\\)的\\(t\\)分布，记作\\(t_n\\)。下图是其密度函数，有人已经证明，当\\(n\\to\\infty\\)时，\\(t\\)分布收敛于正态分布，这也是符合直觉的。

\\[X\\sim N(0,1);\\;Y\\sim \\chi_n^2\\;\\Rightarrow\\;\\dfrac{X}{\\sqrt{Y/n}}\\sim t_n\\tag{16}\\]

　　再回到对式（8）（15）的讨论，显然有式（17）成立，这个结论以后经常用到。关于（17）式我想强调一下，式中好像是用\\(S\\)取代了\\(\\sigma\\)，这只是巧合而已，不要忘了其背后原理还是（8）（15）的结合。是因为\\(\\sigma\\)恰巧被消掉才出现了式（17），遇到更复杂的情况时，要重新仔细计算（下一篇将遇到）。

\\[\\dfrac{\\sqrt{n}(\\bar{X}-\\mu)}{S}\\sim t_{n-1}\\tag{17}\\]

2.3 \\(F\\)分布

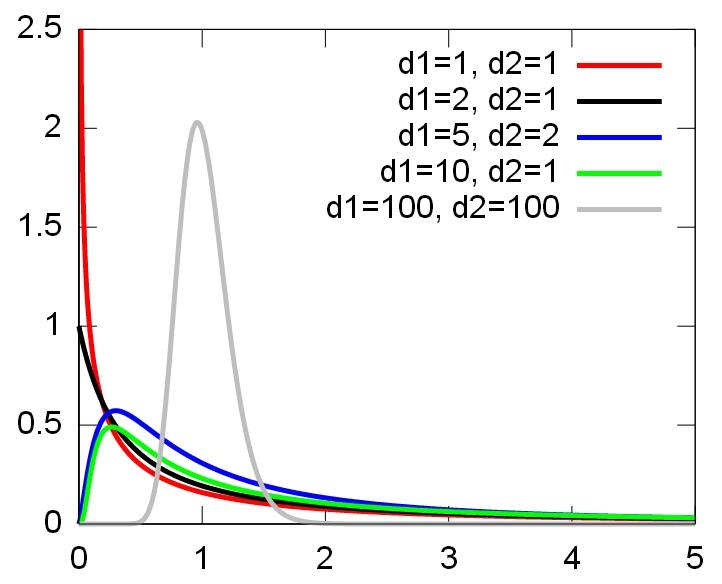
　　还有一种常见的场景，就是比较两个分布的方差比\\(\\sigma_1^2/\\sigma_2^2\\)。同样利用\\(S_i^2\\)近似\\(\\sigma_i^2\\)，并利用公式（15）可以进行类似的讨论。为此，将式（18）中的分布被称为自由度为\\(m,n\\)的\\(F\\)分布，记作\\(F_{m,n}\\)，下图是它的密度函数。

\\[X\\sim\\chi_m^2;\\;Y\\sim\\chi_n^2\\;\\Rightarrow\\;\\dfrac{X/m}{Y/n}\\sim F_{m,n}\\tag{18}\\]

　　回到方差的比较，设\\(X,Y\\)的方差分别为\\(\\sigma_1^2,\\sigma_2^2\\)，样本容量分别为\\(m,n\\)，样本方差分别为\\(S_1^2,S_2^2\\)，容易知道有式（19）成立。

\\[\\dfrac{S_1^2}{S_2^2}\\cdot\\dfrac{\\sigma_2^2}{\\sigma_1^2}\\sim F_{m-1,n-1}\\tag{19}\\]

　　数理统计中使用分布函数时，和概率论中是相反的，即根据概率值来确定随机变量的值。满足\\(P(X>C)=\\alpha\\)的\\(C\\)被称为分布的\\(\\alpha\\)上分位点，对于正态分布和上面的三大分布，\\(\\alpha\\)上分位点分别记作\\(u(\\alpha),\\chi_n^2(\\alpha),t_n(\\alpha),F_{m,n}(\\alpha)\\)。其中\\(t_n,F_{m,n}\\)有式（20）的简单性质，它们在计算和制表中比较有用，证明比较简单，请自行验证。

\\[t_n(1-\\alpha)+t_n(\\alpha)=0;\\;\\;F_{m,n}(\\alpha)\\cdot F_{n,m}(1-\\alpha)=1\\tag{20}\\]