稀疏矩阵的转置运算
Posted 晓乎
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了稀疏矩阵的转置运算相关的知识,希望对你有一定的参考价值。
(1)设m*n 矩阵中有t 个非零元素且t远小于m*n,这样的矩阵称为稀疏矩阵。很多科学管理及工程计算中,常会遇到阶数很高的大型稀疏矩阵。如果按常规分配方法,顺序分配在计算机内,那将是相当浪费内存的。为此提出另外一种存储方法,仅仅存放非零元素。但对于这类矩阵,通常零元素分布没有规律,为了能找到相应的元素,所以仅存储非零元素的值是不够的,还要记下它所在的行和列。于是采取如下方法:将非零元素所在的行、列以及它的值构成一个三元组(i,j,v),然后再按某种规律存储这些三元组,这种方法可以节约存储空间。
将三元组按行优先的顺序,同一行中列号从小到大的规律排列成一个线性表,称为三元组表,采用顺序存储方法存储该表。如下图:

可以将其改写成如下的三元组的形式,同时存储器行、列和值,如下:
|
i |
j |
v |
|
1 |
2 |
12 |
|
1 |
3 |
9 |
|
3 |
1 |
-3 |
|
3 |
6 |
14 |
|
4 |
3 |
24 |
|
5 |
2 |
18 |
|
6 |
1 |
15 |
|
6 |
4 |
-7 |
对应的三元组的数据结构可以写成如下形式的数据结构:
//定义三元组的数据结构类型
typedef struct{
int i,j; //非零元素的行和列
ElemType e; //非零元素的值
}Triple;
//三元组表的存储类型
typedef struct{
int mu,nu,tu; //矩阵的行、列以及非零元的个数
Triple data[MAXSIZE+1]; //三元组表
}Matrix;
(2)、矩阵的转置
要做到转置要做到三点
①、将矩阵的行列值互换
②、将每个三元组的i、j互换
③、重新排列三元组
如下图:

方法一:
①、将矩阵A的行列转化为矩阵B的列和行
②、以B的行(col)为标准依次遍历三元组的列值(j)的值,即矩阵A的第一列的元素必在B的第一行中,依次赋值。
程序如下:
int TransposeSMatrix(Matrix M,Matrix *X)
{
int col,p,q;
//设置转置矩阵的结构
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
q=1;
//遍历每一列的非零元素
for(col=1;col<=M.nu;col++)
//扫描三元组中非零元素的个数
for(p=1;p<=M.tu;p++)
if(M.data[p].j==col) //若找到该列的非零元素,开始对该元素的行列转换
{
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
//继续去对第二个元素进行变化、
q++;
}
}
return OK;
}
方法二:
易看出方法一的时间复杂度主要体现在两次循环上( O(nu*tu) ),当非零元的个数过多的时候(即与mu*nu是同一个数量级的时候),算法的复杂度变为了(o(mu*nu2),虽然此方法在空间上节省了存储空间,但在时间上花费了太大的比重。方法二设置了两个数组num和cpot,num[col]代表矩阵A的每一列的非零元素的个数,cpot[col]表示矩阵A中第col列第一个非零元素的在B对应的三元组的位置,即
cpot[1]=1
cpot[col]=cpot[col-1]+num[col-1] (2<=col<=A.nu)
对应的矩阵A的num和cpot值如下

对应的程序如下所示:
int FastTransposeSMatrix(Matrix M,Matrix *X)
{
int col,k,p,q;
int cpot[10],num[10];
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
//num代表每一行非零元的个数,初始化为0
for(col=1;col<=M.tu;col++)
num[col]=0;
//计算每一列中非零元的个数
for(k=1;k<=M.tu;k++)
num[M.data[k].j]++;
//初始化cpot为1 cpot代表矩阵M中第col列的第一个非零元素的转置后矩阵X.data的位置
cpot[1]=1;
for(col=2;col<=M.nu;col++)
cpot[col]=cpot[col-1]+num[col-1];
for(p=1;p<=M.tu;p++)
{
col=M.data[p].j;
q=cpot[col];
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
cpot[col]++;
}
}
return OK;
}
完整程序如下:
#include<stdio.h>
#define OK 1
#define MAXSIZE 100
typedef int ElemType;
//定义三元组的数据结构类型
typedef struct{
int i,j; //非零元素的行和列
ElemType e; //非零元素的值
}Triple;
//三元组表的存储类型
typedef struct{
int mu,nu,tu; //矩阵的行、列以及非零元的个数
Triple data[MAXSIZE+1]; //三元组表
}Matrix;
int TransposeSMatrix(Matrix M,Matrix *X)
{
int col,p,q;
//设置转置矩阵的结构
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
q=1;
//遍历每一列的非零元素
for(col=1;col<=M.nu;col++)
//扫描三元组中非零元素的个数
for(p=1;p<=M.tu;p++)
if(M.data[p].j==col) //若找到该列的非零元素,开始对该元素的行列转换
{
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
//继续去对第二个元素进行变化、
q++;
}
}
return OK;
}
int FastTransposeSMatrix(Matrix M,Matrix *X)
{
int col,k,p,q;
int cpot[10],num[10];
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
//num代表每一行非零元的个数,初始化为0
for(col=1;col<=M.tu;col++)
num[col]=0;
//计算每一列中非零元的个数
for(k=1;k<=M.tu;k++)
num[M.data[k].j]++;
//初始化cpot为1 cpot代表矩阵M中第col列的第一个非零元素的转置后矩阵X.data的位置
cpot[1]=1;
for(col=2;col<=M.nu;col++)
cpot[col]=cpot[col-1]+num[col-1];
for(p=1;p<=M.tu;p++)
{
col=M.data[p].j;
q=cpot[col];
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
cpot[col]++;
}
}
return OK;
}
//创建系数矩阵,用三元组法表示
void Create(Matrix *M)
{
int i;
printf("请分别输入非零元素的行(mu)、列(nu)以及非零元素的个数(ti):");
scanf("%d %d %d",&M->mu,&M->nu,&M->tu);
printf("请按以下格式输入非零元素(行 列 元素值):\\n");
for(i=1;i<=M->tu;i++)
scanf("%d %d %d",&M->data[i].i,&M->data[i].j,&M->data[i].e);
}
//以矩阵的形式输出三元组表示存储的稀疏矩阵
void print(Matrix M)
{
int i,j,k;
//二维数组初始化
int a[10][10]={0};
for(k=1;k<=M.tu;k++)
{
i=M.data[k].i;
j=M.data[k].j;
a[i][j]=M.data[k].e;
}
printf("Matrix is : \\n");
for(i=1;i<=M.mu;i++)
{
for(j=1;j<=M.nu;j++)
printf("%4d",a[i][j]);
printf("\\n");
}
}
void main()
{
Matrix M,X;
Create(&M);
print(M);
FastTransposeSMatrix(M,&X);
print(X);
}
运行结构如下:
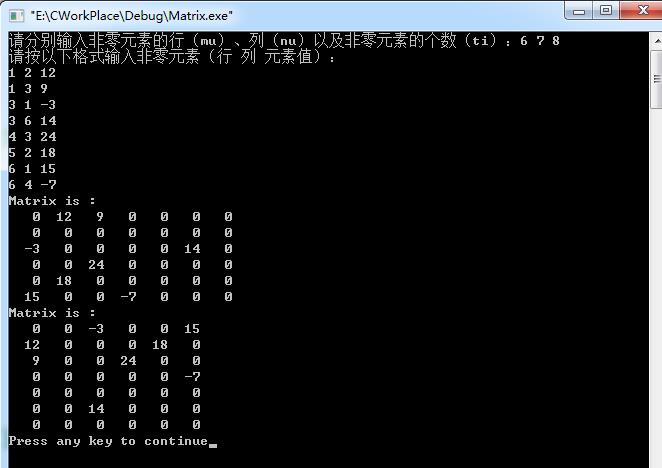
以上是关于稀疏矩阵的转置运算的主要内容,如果未能解决你的问题,请参考以下文章