MATLAB 稀疏矩阵

Posted 2023-05-11

X 是一个维度很高的向量，要实现X乘以X的转置，直接乘MATLAB会报错Out of memory。。怎么做乘法之后转换成稀疏矩阵？

参考技术A 向量是一维的，维度怎么会很高？X是矩阵，则先稀疏化，Y=sparse(X);再乘，Z=Y*Y‘；结果Z就是稀疏矩阵追问

X是一个向量，，，向量维度很高，，X乘以X的转置之后得到一个维度很高的矩阵。。这个过程中out of memory

MATLAB 电力系统潮流计算（采用稀疏矩阵，可计算1000节点）

MATLAB电力系统潮流计算

用MATLAB利用牛顿-拉夫逊法计算电科院22节点系统（使用稀疏技术），计算出各节点的电压相角、各支路的功率等。使用了稀疏计算技术，能计算1000节点以上的系统，且计算时间小于1秒。

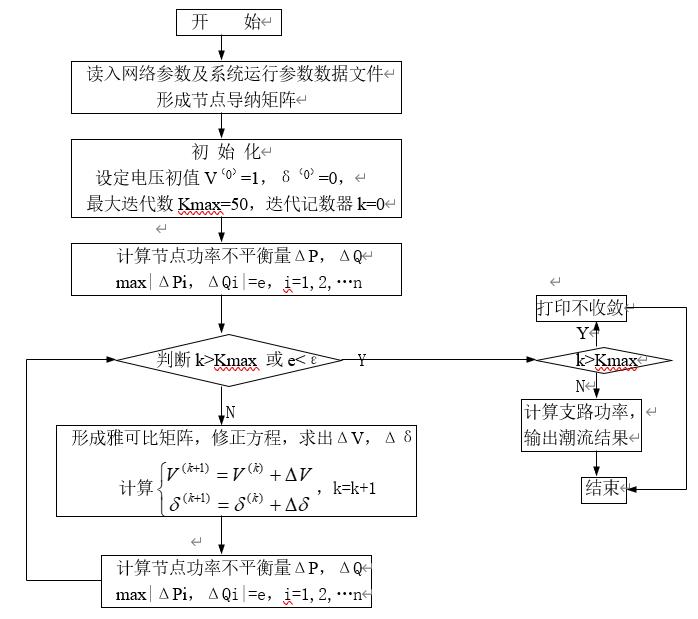
计算思路

1. 形成节点导纳矩阵，分析各节点的类型，找出待求量；
2. 设定各节点电压的初值，并给定迭代误差判据；；
3. 计算不平衡量；
4. 求修正方程的系数矩阵，即雅可比矩阵的各元素；
5. 形成雅可比矩阵，求解修正方程，得到各节点电压变化量；
6. 计算各节点电压新值；
7. 检查是否收敛，如不收敛，则运用各节点电压新值自第3步开始下一次迭代；
8. 计算平衡节点功率和线路功率。

结果展示

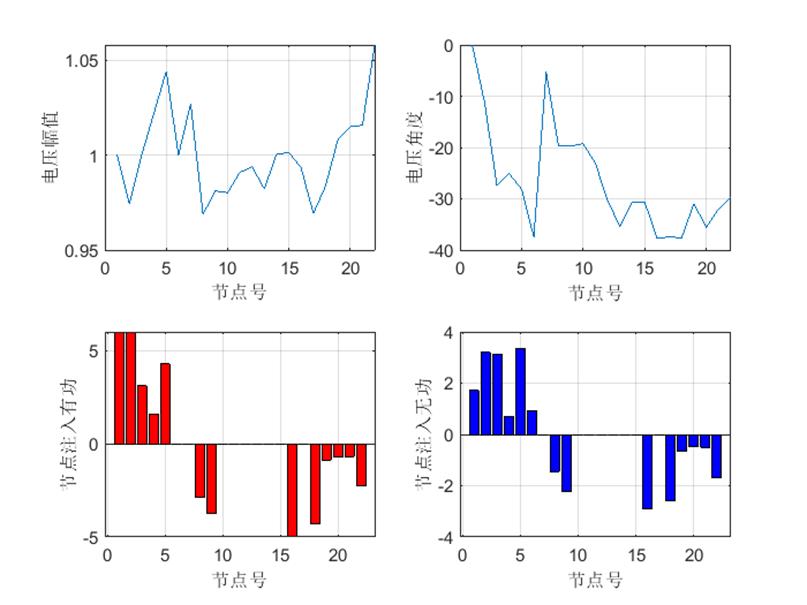
22节点网络潮流计算

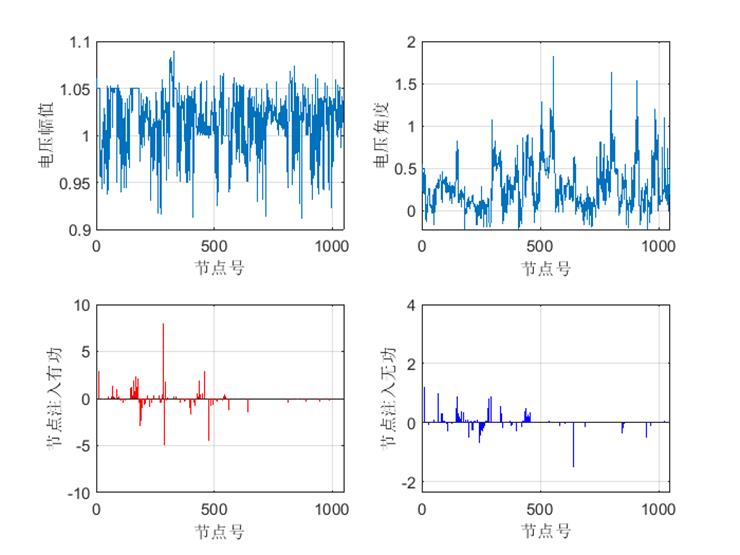
1047节点潮流计算

部分代码

读取文件

%% 取数据文件和参数
[open_filename] = uigetfile('.TXT');
data=dlmread(open_filename);
node_num=data(1,1);                                                        %节点数
branchnum=data(1,2);                                                       %支路数
balancenode=data(1,3);                                                     %平衡节点号数
v_balancenode=data(1,4);                                                   %平衡节点电压
base_power=data(1,6);                                                      %基准功率
convergence_accuracy=data(1,7);                                            %运算精度
index=find(data(:,1)==0);                                                  %index存放矩阵中第一列为0的元素（区分各块参数）
Line=data(index(1)+1:index(2)-1,:);                                        %线路为第一块
Line_ground=data(index(2)+1:index(3)-1,:);                                 %对地支路为第二块
Transformer=data(index(3)+1:index(4)-1,1:6);                               %变压器为第三块
PQ=data(index(4)+1:index(5)-1,:);                                          %PQ节点为第四块
PV=data(index(5)+1:index(6)-1,:);                                          %PV节点为第五块
PV_num=PV(:,1);                                                            %PV节点数
R=Line(:,4);X=1j*Line(:,5);	B=1j*Line(:,6);Z=R+X;Line_Y=1./Z;              %Y是Z的逆矩阵,线路参数
Rt=Transformer(:,4);	Xt=Transformer(:,5);	k=Transformer(:,6);        %变压器参数
Gt=Rt./(Rt.*Rt+Xt.*Xt);Bt=-Xt./(Rt.*Rt+Xt.*Xt);
Yt=Gt+1j.*Bt; Yt2=Yt./k; Yt3=Yt./k./k;                                     %变压器等值电路参数
G_ground=1j*Line_ground(:,2);                                              %对地支路参数
Nonzero_num=node_num+2*(size(Line,1)+size(Transformer,1));                 %非零元素：对角线+2*（线路+变压器）

形成节点导纳矩阵（应用稀疏矩阵）

tic;                                                                       %计时
Y=spalloc(node_num,node_num,Nonzero_num);                                  %创建一个节点数*节点数的全零稀疏矩阵Y，该矩阵具有Nonzero_num个非零值的空间
node_i=Line(:,2);node_j=Line(:,3);                                         %节点i、j
Y=Y-sparse(node_i,node_j,Line_Y,node_num,node_num)-sparse(node_j,node_i,Line_Y,node_num,node_num);   %把互导纳放进Y的（node_i,node_j）和（node_j,node_i）位置
Y_new=Y;
i=1:node_num;                                                              %创建一个由1到22的行向量
Y=Y-sparse(i,i,sum(Y_new,2),node_num,node_num);                            %把自导纳放进Y的（i,i）位置

node_i=Transformer(:,2);node_j=Transformer(:,3);                           %将变压器等值参数电路放进矩阵
Y=Y-sparse(node_i,node_j,Yt2,node_num,node_num)-sparse(node_j,node_i,Yt2,node_num,node_num);  %互导纳
Y=Y+sparse(node_i,node_i,Yt3,node_num,node_num)+sparse(node_j,node_j,Yt,node_num,node_num);   %自导纳

i=Line_ground(:,1);
Y=Y+sparse(i,i,G_ground,node_num,node_num);                                %自导纳放入对地支路的G
i=Line(:,2);
Y=Y+sparse(i,i,B,node_num,node_num);                                       %自导纳放入i支路的B
i=Line(:,3);
Y=Y+sparse(i,i,B,node_num,node_num);                                       %自导纳放入j支路的B
Y_abs=abs(full(Y));							                               %形成导纳矩阵的幅值矩阵
Y_angle=angle(full(Y));							                           %导纳矩阵的相角矩阵

迭代设置

V=ones(node_num,1); 					                                   %计算启动的电压幅值为1
deta=zeros(node_num,1);                                                    %相角为0
%deta=ones(node_num,1)*100*pi/180;                                          %问9：平衡节点相角设为100°
V(PV(:,1),1)=PV(:,2);						                               %PV节点电压设置
V(balancenode)=v_balancenode;				                               %平衡节点电压设置
JDV=[deta;V];								                               %修正量的向量
P=(PQ(:,2)-PQ(:,4))/base_power;			                                   %取标幺值
Q=(PQ(:,3)-PQ(:,5))/base_power;

开始迭代的（部分代码）

count_max=15;                                                              %最大迭代次数为count_max
for count=0:count_max
    %% 功率方程不平衡量
    A=ones(node_num,1);
    deta_ij=deta*A'-A*deta';                                               %deta(ij)=deta(i)-deta(j)
    Pi_0=sum(diag(V)*(real(Y).*cos(deta_ij)+imag(Y).*sin(deta_ij))*diag(V),2);%计算Pi
    dP=P-Pi_0;                                                             %计算dPi
    Qi_0=sum(diag(V)*(real(Y).*sin(deta_ij)-imag(Y).*cos(deta_ij))*diag(V),2);%计算Qi
    dQ=Q-Qi_0;                                                             %计算dQi
    dP(balancenode)=0;dQ(balancenode)=0;                                   %平衡节点的dP,Q设为0
    dQ(PV(:,1))=0;					                                       %pv节点的不平衡量dQ设为0
    JDPQ=[dP;dQ];                                                          %修正方程的左边，dp，dq组成的列向量
    %% 雅可比矩阵（应用稀疏矩阵）非对角元部分
    [Jacobian_i,Jacobian_j]=find(Y);Jacobian_n=size(Jacobian_i,1);         %Y中非零元素位置放到Jacobian_i,Jacobian_j中,Jacobian_n为Jacobian_i的行数

判断收敛条件

    %% 判断是否收敛
    %DV=V.*delta_V;    
    %Ddelta=[delta_deta;DV];
    delta_V=delta(node_num+1:2*node_num).*V;
    V=V-delta_V;
    deta=deta-delta(1:node_num);
    if max(abs(delta_V))<convergence_accuracy                              %达到收敛精度
        break
    end
    time=toc;

输出结果

%% 运行结束输出结果
disp('迭代次数:'),disp(count);
disp('迭代用时：'),disp(time);
if count>=count_max                                                        %不收敛
    disp('超过设置的最大迭代次数，结果不收敛！')
else
    disp('结果收敛，结果为：');jd_angle=deta.*180/pi;                       %相角弧度制转换为角度制
    disp('各节点电压：（幅值，相角）'),disp([V,jd_angle]);
    n_Line=size(Line,1);                                                   %线路参数长度
    n_trsnsformer=size(Transformer,1);                                     %变压器参数长度
    S1=zeros(node_num);
    S2=zeros(node_num);

计算平衡节点功率、各支路功率、变压器支路功率等等

%% 计算平衡节点功率
    Sb=0;
    for t=1:node_num
        Ui=V(t,1)*cos(deta(t,1))+1j*V(t,1)*sin(deta(t,1));    
        Us=V(balancenode,1)*cos(deta(balancenode,1))+1j*V(balancenode,1)*sin(deta(balancenode,1));
        Sb=Sb+conj(Y(balancenode,t))*conj(Ui);
    end
    disp('平衡节点功率：'),Sb=Us*Sb

%% 画图显示结果
    subplot(2,2,1),plot(1:node_num,V)
    xlabel('节点号');ylabel('电压幅值');grid on;
    subplot(2,2,2),plot(1:node_num,jd_angle)
    xlabel('节点号');ylabel('电压角度');grid on;
    subplot(2,2,3),bar(P,'r');
    xlabel('节点号');ylabel('节点注入有功');grid on;
    subplot(2,2,4);bar(Q,'b');    
    xlabel('节点号');ylabel('节点注入无功');grid on;
end

完整源代码可私聊。

可转下载区