关于稀疏矩阵三元组的转置
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了关于稀疏矩阵三元组的转置相关的知识,希望对你有一定的参考价值。
直接上代码:
#include<stdio.h>
#include<alloc.h>
#define ERROR 0
#define OK 1
#define EQUAL 1
#define OVERFLOW -1
#define MAXSIZE 12500
struct Triple
int i;
int j;
int data;
;
typedef struct Triple ElemType;
struct Mastrix
ElemType *e;
int mu,nu,tu;
;
typedef struct Mastrix mastrix;
typedef struct Mastrix *list;
void InitMastrix(list l)
l->e=(list)malloc((MAXSIZE+1)*sizeof(ElemType));
if(!l) exit(OVERFLOW);
void CreatMastrix(list l)
int i;
int a,b,c;
printf("please input the mastrix's mu,nu and tu\n");
scanf("%d,%d,%d",&a,&b,&c);
l->mu=a;
l->nu=b;
l->tu=c;
printf("please creat the mastrix:\n");
for(i=0;i<c;i++)
printf("please input %dth data's information:\n",i+1);
scanf("%d,%d,%d",&l->e[i].i,&l->e[i].j,&l->e[i].data);
void FastTransposeMatrix(list l,list m)
int num[100],cpot[100],col,p,q;
m->nu=l->mu;m->mu=l->nu;m->tu=l->tu;
for(p=1;p<=l->nu;p++) num[p]=0;
for(p=1;p<=l->tu;p++) ++num[l->e[p].j];
cpot[1]=1;
for(p=2;p<=l->nu;p++) cpot[p]=cpot[p-1]+num[p-1];
for(p=1;p<=l->tu;p++)
col=l->e[p].j;
q=cpot[col];
m->e[q].i=l->e[p].j;
m->e[q].j=l->e[p].i;
m->e[q].data=l->e[p].data;
++cpot[col];
void Show(list l)
int i,j,k=0;
for(i=0;i<l->mu;i++)
printf("\n");
for(j=0;j<l->nu;j++)
if((i+1)==l->e[k].i&&(j+1)==l->e[k].j)
printf("%d\t",l->e[k].data);
k++;
else printf("0\t");
main()
list l,m;
InitMastrix(l);
CreatMastrix(l);
Show(l);
getch();
InitMastrix(m);
FastTransposeMatrix(l,m);
Show(m);
getch();
转置全部输出0....
求错在何处
不好意思
这数据结构的题我都是在TC上运行的。。。
一楼说的那里,我的确错了,疏忽了,但是不是造成转置后全部输出0的原因。
我想是我的算法出了差错。
#include <iostream>
#include <iomanip>
using namespace std;
const int MAXSIZE=100; // 定义非零元素的对多个数
const int MAXROW=10; // 定义数组的行数的最大值
typedef struct // 定义三元组的元素
int i,j;
int e;
Triple;
typedef struct // 定义普通三元组对象
Triple data[MAXSIZE+1];
int mu,nu,tu;
TSMatrix;
typedef struct // 定义带链接信息的三元组对象
Triple data[MAXSIZE+2];
int rpos[MAXROW+1];
int mu,nu,tu;
RLSMatrix;
template <class P>
bool InPutTSMatrix(P & T,int y) //输入矩阵,按三元组格式输入
cout<<"输入矩阵的行,列和非零元素个数:"<<endl;
cin>>T.mu>>T.nu>>T.tu;
cout<<"请输出非零元素的位置和值:"<<endl;
int k=1;
for(;k<=T.tu;k++)
cin>>T.data[k].i>>T.data[k].j>>T.data[k].e;
return true;
template <class P>
bool OutPutSMatrix(P T) // 输出矩阵,按标准格式输出
int m,n,k=1;
for(m=0;m<T.mu;m++)
for(n=0;n<T.nu;n++)
if((T.data[k].i-1)==m&&(T.data[k].j-1)==n)
cout.width(4);
cout<<T.data[k++].e;
else
cout.width(4); cout<<"0";
cout<<endl;
return true;
// 求矩阵的转置矩阵
bool TransposeSMatrix( )
TSMatrix M,T; //定义预转置的矩阵
InPutTSMatrix(M, 0); //输入矩阵
int num[MAXROW+1];
int cpot[MAXROW+1]; // 构建辅助数组
int q,p,t;
T.tu=M.tu; T.mu=M.nu; T.nu=M.mu;
if(T.tu)
for(int col=1;col<=M.nu;col++) num[col]=0;
for(t=1;t<=M.tu;t++) ++num[M.data[t].j];
cpot[1]=1;
for(int i=2;i<=M.nu;i++) cpot[i]=cpot[i-1]+num[i-1]; // 求出每一列中非零元素在三元组中出现的位置
for(p=1;p<=M.tu;p++)
col=M.data[p].j; q=cpot[col];
T.data[q].i=col; T.data[q].j=M.data[p].i;
T.data[q].e=M.data[p].e; ++cpot[col];
cout<<"输入矩阵的转置矩阵为"<<endl;
OutPutSMatrix(T);
return true;
bool Count(RLSMatrix &T)
int num[MAXROW+1];
for(int col=1;col<=T.mu;col++) num[col]=0;
for(col=1;col<=T.tu;col++) ++num[T.data[col].i];
T.rpos[1]=1;
for(int i=2;i<=T.mu;i++) T.rpos[i]=T.rpos[i-1]+num[i-1]; // 求取每一行中非零元素在三元组中出现的位置
return true;
// 两个矩阵相乘
bool MultSMatrix ( )
RLSMatrix M,N,Q; // 构建三个带“链接信息”的三元组表示的数组
InPutTSMatrix(M,1); // 用普通三元组形式输入数组
InPutTSMatrix(N,1);
Count(M); Count(N);
if(M.nu!=N.mu) return false;
Q.mu=M.mu; Q.nu=N.nu; Q.tu=0; // Q初始化
int ctemp[MAXROW+1]; // 辅助数组
int arow,tp,p,brow,t,q,ccol;
if(M.tu*N.tu) // Q是非零矩阵
for( arow=1;arow<=M.mu;arow++)
///memset(ctemp,0,N.nu);
for(int x=1;x<=N.nu;x++) // 当前行各元素累加器清零
ctemp[x]=0;
Q.rpos[arow]=Q.tu+1; // 当前行的首个非零元素在三元组中的位置为此行前所有非零元素+1
if(arow<M.mu) tp=M.rpos[arow+1];
else tp=M.tu+1;
for(p=M.rpos[arow];p<tp;p++) // 对当前行每个非零元素进行操作
brow=M.data[p].j; // 在N中找到i值也操作元素的j值相等的行
if(brow<N.mu) t=N.rpos[brow+1];
else t=N.tu+1;
for(q=N.rpos[brow];q<t;q++) // 对找出的行当每个非零元素进行操作
ccol=N.data[q].j;
ctemp[ccol] += M.data[p].e*N.data[q].e; // 将乘得到对应值放在相应的元素累加器里面
for(ccol=1;ccol<=Q.nu;ccol++) // 对已经求出的累加器中的值压缩到Q中
if(ctemp[ccol])
if(++Q.tu>MAXSIZE) return false;
Q.data[Q.tu].e=ctemp[ccol];
Q.data[Q.tu].i=arow;
Q.data[Q.tu].j=ccol;
OutPutSMatrix(Q);
return true;
typedef struct OLNode // 定义十字链表元素
int i,j;
int e;
struct OLNode *right,*down; // 该非零元所在行表和列表的后继元素
OLNode,*OLink;
typedef struct // 定义十字链表对象结构体
OLink *rhead,*chead;
int mu,nu,tu; // 系数矩阵的行数,列数,和非零元素个数
CrossList;
bool CreateSMatrix_OL(CrossList & M) // 创建十字链表
int x,y,m;
cout<<"请输入矩阵的行,列,及非零元素个数"<<endl;
cin>>M.mu>>M.nu>>M.tu;
if(!(M.rhead=(OLink*)malloc((M.mu+1)*sizeof(OLink)))) exit(0);
if(!(M.chead=(OLink*)malloc((M.nu+1)*sizeof(OLink)))) exit(0);
for(x=0;x<=M.mu;x++)
M.rhead[x]=NULL; // 初始化各行,列头指针,分别为NULL
for(x=0;x<=M.nu;x++)
M.chead[x]=NULL;
cout<<"请按三元组的格式输入数组:"<<endl;
for(int i=1;i<=M.tu;i++)
cin>>x>>y>>m; // 按任意顺序输入非零元,(普通三元组形式输入)
OLink p,q;
if(!(p=(OLink)malloc(sizeof(OLNode)))) exit(0); // 开辟新节点,用来存储输入的新元素
p->i=x; p->j=y; p->e=m;
if(M.rhead[x]==NULL||M.rhead[x]->j>y)
p->right=M.rhead[x]; M.rhead[x]=p;
else
for(q=M.rhead[x];(q->right)&&(q->right->j<y);q=q->right); // 查找节点在行表中的插入位置
p->right=q->right; q->right=p; // 完成行插入
if(M.chead[y]==NULL||M.chead[y]->i>x)
p->down=M.chead[y]; M.chead[y]=p;
else
for(q=M.chead[y];(q->down)&&(q->down->i<x);q=q->down); // 查找节点在列表中的插入位置
p->down=q->down; q->down=p; // 完成列插入
return true;
bool OutPutSMatrix_OL(CrossList T) // 输出十字链表,用普通数组形式输出
for(int i=1;i<=T.mu;i++)
OLink p=T.rhead[i];
for(int j=1;j<=T.nu;j++)
if((p)&&(j==p->j))
cout<<setw(3)<<p->e; p=p->right;
else
cout<<setw(3)<<"0";
cout<<endl;
return true;
//矩阵的加法
bool AddSMatrix()
CrossList M,N; // 创建两个十字链表对象,并初始化
CreateSMatrix_OL(M);
CreateSMatrix_OL(N);
cout<<"输入的两矩阵的和矩阵为:"<<endl;
OLink pa,pb,pre ,hl[MAXROW+1]; //定义辅助指针,pa,pb分别为M,N当前比较的元素,pre为pa的前驱元素
for(int x=1;x<=M.nu;x++) hl[x]=M.chead[x];
for(int k=1;k<=M.mu;k++) // 对M的每一行进行操作
pa=M.rhead[k]; pb=N.rhead[k]; pre=NULL;
while(pb) // 把N中此行的每个元素取出,
OLink p;
if(!(p=(OLink)malloc(sizeof(OLNode)))) exit(0); // 开辟新节点,存储N中取出的元素
p->e=pb->e; p->i=pb->i; p->j=pb->j;
if(NULL==pa||pa->j>pb->j) // 当M此行已经检查完或者pb因该放在pa前面
if(NULL==pre)
M.rhead[p->i]=p;
else
pre->right=p;
p->right=pa; pre=p;
if(NULL==M.chead[p->j]) // 进行列插入
M.chead[p->j]=p; p->down=NULL;
else
p->down=hl[p->j]->down; hl[p->j]->down=p;
hl[p->j]=p;
pb=pb->right;
else
if((NULL!=pa)&&pa->j<pb->j) // 如果此时的pb元素因该放在pa后面,则取以后的pa再来比较
pre=pa; pa=pa->right;
else
if(pa->j==pb->j) // 如果pa,pb位于同一个位置上,则将值相加
pa->e += pb->e;
if(!pa->e) // 如果相加后的和为0,则删除此节点,同时改变此元素坐在行,列的前驱元素的相应值
if(NULL==pre) // 修改行前驱元素值
M.rhead[pa->i]=pa->right;
else
pre->right=pa->right;
p=pa; pa=pa->right;
if(M.chead[p->j]==p) M.chead[p->j]=hl[p->j]=p->down; // 修改列前驱元素值
else
hl[p->j]->down=p->down;
free(p); pb=pb->right;
else
pa=pa->right; pb=pb->right;
OutPutSMatrix_OL(M);
return true;
int main()
cout.fill('*');
cout<<setw(80)<<'*';
cout.fill(' ');
// system("color 0C");
cout<<setw(50)<<"***欢迎使用矩阵运算程序***"<<endl; //输出头菜单
cout.fill('*');
cout<<setw(80)<<'*';
cout.fill(' ');
cout<<"请选择要进行的操作:"<<endl;
cout<<"1:矩阵的转置。"<<endl;
cout<<"2:矩阵的加(减)法。"<<endl;
cout<<"3:矩阵的乘法。"<<endl;
cout<<"4:推出程序。"<<endl;
char c=getchar();
if(c=='1')
TransposeSMatrix( ); //调用矩阵转置函数
else
if(c=='2')
AddSMatrix(); //调用矩阵相加函数
else
if(c=='3')
MultSMatrix (); //调用矩阵相乘函数
else
exit(0); //退出
return 0;
参考技术A l->e=(list)malloc((MAXSIZE+1)*sizeof(ElemType));// 这句在VC不能通过编译,因为e是elemtype类型,分配的空间是list类型,不匹配。
//头文件也有出入,修改后运行直接出错。。 看来不同环境比较难搞
稀疏矩阵的转置运算
(1)设m*n 矩阵中有t 个非零元素且t远小于m*n,这样的矩阵称为稀疏矩阵。很多科学管理及工程计算中,常会遇到阶数很高的大型稀疏矩阵。如果按常规分配方法,顺序分配在计算机内,那将是相当浪费内存的。为此提出另外一种存储方法,仅仅存放非零元素。但对于这类矩阵,通常零元素分布没有规律,为了能找到相应的元素,所以仅存储非零元素的值是不够的,还要记下它所在的行和列。于是采取如下方法:将非零元素所在的行、列以及它的值构成一个三元组(i,j,v),然后再按某种规律存储这些三元组,这种方法可以节约存储空间。
将三元组按行优先的顺序,同一行中列号从小到大的规律排列成一个线性表,称为三元组表,采用顺序存储方法存储该表。如下图:

可以将其改写成如下的三元组的形式,同时存储器行、列和值,如下:
|
i |
j |
v |
|
1 |
2 |
12 |
|
1 |
3 |
9 |
|
3 |
1 |
-3 |
|
3 |
6 |
14 |
|
4 |
3 |
24 |
|
5 |
2 |
18 |
|
6 |
1 |
15 |
|
6 |
4 |
-7 |
对应的三元组的数据结构可以写成如下形式的数据结构:
//定义三元组的数据结构类型
typedef struct{
int i,j; //非零元素的行和列
ElemType e; //非零元素的值
}Triple;
//三元组表的存储类型
typedef struct{
int mu,nu,tu; //矩阵的行、列以及非零元的个数
Triple data[MAXSIZE+1]; //三元组表
}Matrix;
(2)、矩阵的转置
要做到转置要做到三点
①、将矩阵的行列值互换
②、将每个三元组的i、j互换
③、重新排列三元组
如下图:

方法一:
①、将矩阵A的行列转化为矩阵B的列和行
②、以B的行(col)为标准依次遍历三元组的列值(j)的值,即矩阵A的第一列的元素必在B的第一行中,依次赋值。
程序如下:
int TransposeSMatrix(Matrix M,Matrix *X)
{
int col,p,q;
//设置转置矩阵的结构
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
q=1;
//遍历每一列的非零元素
for(col=1;col<=M.nu;col++)
//扫描三元组中非零元素的个数
for(p=1;p<=M.tu;p++)
if(M.data[p].j==col) //若找到该列的非零元素,开始对该元素的行列转换
{
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
//继续去对第二个元素进行变化、
q++;
}
}
return OK;
}
方法二:
易看出方法一的时间复杂度主要体现在两次循环上( O(nu*tu) ),当非零元的个数过多的时候(即与mu*nu是同一个数量级的时候),算法的复杂度变为了(o(mu*nu2),虽然此方法在空间上节省了存储空间,但在时间上花费了太大的比重。方法二设置了两个数组num和cpot,num[col]代表矩阵A的每一列的非零元素的个数,cpot[col]表示矩阵A中第col列第一个非零元素的在B对应的三元组的位置,即
cpot[1]=1
cpot[col]=cpot[col-1]+num[col-1] (2<=col<=A.nu)
对应的矩阵A的num和cpot值如下

对应的程序如下所示:
int FastTransposeSMatrix(Matrix M,Matrix *X)
{
int col,k,p,q;
int cpot[10],num[10];
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
//num代表每一行非零元的个数,初始化为0
for(col=1;col<=M.tu;col++)
num[col]=0;
//计算每一列中非零元的个数
for(k=1;k<=M.tu;k++)
num[M.data[k].j]++;
//初始化cpot为1 cpot代表矩阵M中第col列的第一个非零元素的转置后矩阵X.data的位置
cpot[1]=1;
for(col=2;col<=M.nu;col++)
cpot[col]=cpot[col-1]+num[col-1];
for(p=1;p<=M.tu;p++)
{
col=M.data[p].j;
q=cpot[col];
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
cpot[col]++;
}
}
return OK;
}
完整程序如下:
#include<stdio.h>
#define OK 1
#define MAXSIZE 100
typedef int ElemType;
//定义三元组的数据结构类型
typedef struct{
int i,j; //非零元素的行和列
ElemType e; //非零元素的值
}Triple;
//三元组表的存储类型
typedef struct{
int mu,nu,tu; //矩阵的行、列以及非零元的个数
Triple data[MAXSIZE+1]; //三元组表
}Matrix;
int TransposeSMatrix(Matrix M,Matrix *X)
{
int col,p,q;
//设置转置矩阵的结构
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
q=1;
//遍历每一列的非零元素
for(col=1;col<=M.nu;col++)
//扫描三元组中非零元素的个数
for(p=1;p<=M.tu;p++)
if(M.data[p].j==col) //若找到该列的非零元素,开始对该元素的行列转换
{
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
//继续去对第二个元素进行变化、
q++;
}
}
return OK;
}
int FastTransposeSMatrix(Matrix M,Matrix *X)
{
int col,k,p,q;
int cpot[10],num[10];
X->mu=M.nu;
X->nu=M.mu;
X->tu=M.tu;
//矩阵中有非零元素才开始去完成转置工作,否则没有意义
if(X->tu)
{
//num代表每一行非零元的个数,初始化为0
for(col=1;col<=M.tu;col++)
num[col]=0;
//计算每一列中非零元的个数
for(k=1;k<=M.tu;k++)
num[M.data[k].j]++;
//初始化cpot为1 cpot代表矩阵M中第col列的第一个非零元素的转置后矩阵X.data的位置
cpot[1]=1;
for(col=2;col<=M.nu;col++)
cpot[col]=cpot[col-1]+num[col-1];
for(p=1;p<=M.tu;p++)
{
col=M.data[p].j;
q=cpot[col];
X->data[q].i=M.data[p].j;
X->data[q].j=M.data[p].i;
X->data[q].e=M.data[p].e;
cpot[col]++;
}
}
return OK;
}
//创建系数矩阵,用三元组法表示
void Create(Matrix *M)
{
int i;
printf("请分别输入非零元素的行(mu)、列(nu)以及非零元素的个数(ti):");
scanf("%d %d %d",&M->mu,&M->nu,&M->tu);
printf("请按以下格式输入非零元素(行 列 元素值):\\n");
for(i=1;i<=M->tu;i++)
scanf("%d %d %d",&M->data[i].i,&M->data[i].j,&M->data[i].e);
}
//以矩阵的形式输出三元组表示存储的稀疏矩阵
void print(Matrix M)
{
int i,j,k;
//二维数组初始化
int a[10][10]={0};
for(k=1;k<=M.tu;k++)
{
i=M.data[k].i;
j=M.data[k].j;
a[i][j]=M.data[k].e;
}
printf("Matrix is : \\n");
for(i=1;i<=M.mu;i++)
{
for(j=1;j<=M.nu;j++)
printf("%4d",a[i][j]);
printf("\\n");
}
}
void main()
{
Matrix M,X;
Create(&M);
print(M);
FastTransposeSMatrix(M,&X);
print(X);
}
运行结构如下:
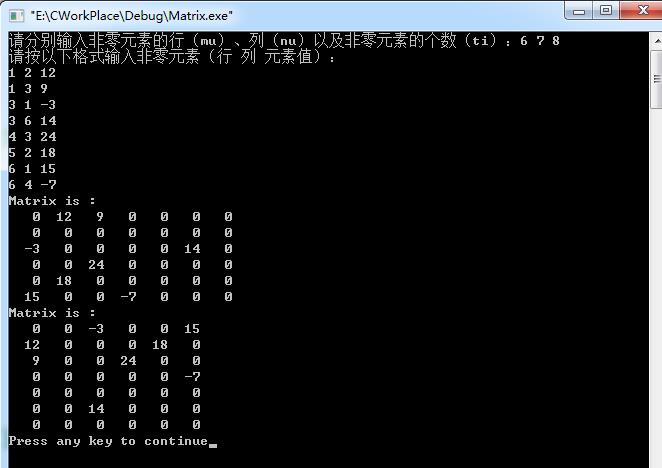
以上是关于关于稀疏矩阵三元组的转置的主要内容,如果未能解决你的问题,请参考以下文章