算法设计与分析基础10深度优先遍历

Posted 2020-09-19 cutter_point

package cn.xf.algorithm.ch03;

import org.junit.Test;

/**
 * 深度优先遍历
 * @author xiaof
 *
 */
public class DFS {

	public void deepFirstSearch(int graph[][], char points[], int marks[]){
		//吧所有点设置为0，表示还未访问过
		for(int i = 0; i < marks.length; ++i) {
			marks[i] = 0;
		}
		//遍历所有节点，挨个访问
		for(int i = 0; i < points.length; ++i) {
			//判断这个节点没有被访问过
			if(marks[i] == 0) {
//				System.out.println(" => " + key);
				//表示当前节点已经被遍历
				marks[i] = 1;
				//深度遍历，这里是设置开始的节点
				StringBuilder path = new StringBuilder(points[i] + "");
				dfsw(graph, points, marks, i, path);
				System.out.println(path.toString());
			}
		}
	}
	
	//深度遍历
	public void dfsw(int graph[][], char points[], int marks[], int curIndex, StringBuilder path){
		//遍历其他节点，判断是否相连
		for(int i = 0; i < marks.length; ++i) {
			//遍历序列，并且获取对应的位置index
			int curNum = graph[curIndex][i];
			if(marks[i] == 0 && curNum != 0) {
				//这个节点还没有被访问过,并且这个节点可达
//				System.out.println(" => " + points[i]);
				path.append(" => " + points[i]);
				marks[i] = 1;
				//递归到下一个
				dfsw(graph, points, marks, i, path);
			}
		}
	}

	@Test
	public void test1(){
		
		DFS dfs = new DFS();
		//a,b,c,d,e,f,g,h,i,j一共10个节点，两颗树
		//以下是矩阵图，0表示不相连，1表示相连，节点本身自己到自己为0
		int graph[][] = {
			//   a,b,c,d,e,f,g,h,i,j
				{0,0,1,1,1,0,0,0,0,0},  //a 到其他节点
				{0,0,0,0,1,1,0,0,0,0},	//b 到其他节点
				{1,0,0,1,0,1,0,0,0,0},	//c 到其他节点
				{1,0,1,0,0,0,0,0,0,0},	//d 到其他节点
				{1,1,0,0,0,1,0,0,0,0},	//e 到其他节点
				{0,1,1,0,1,0,0,0,0,0},	//f 到其他节点
				{0,0,0,0,0,0,0,1,0,1},	//g 到其他节点
				{0,0,0,0,0,0,1,0,1,0},	//h 到其他节点
				{0,0,0,0,0,0,0,1,0,1},	//i 到其他节点
				{0,0,0,0,0,0,1,0,1,0}	//j 到其他节点
		};
		char points[] = {\'A\', \'B\', \'C\', \'D\', \'E\', \'F\', \'G\', \'H\', \'I\', \'J\'};
		int marks[] = {0,0,0,0,0,0,0,0,0,0};
		dfs.deepFirstSearch(graph, points, marks);
		
		
	}
}

　　

 

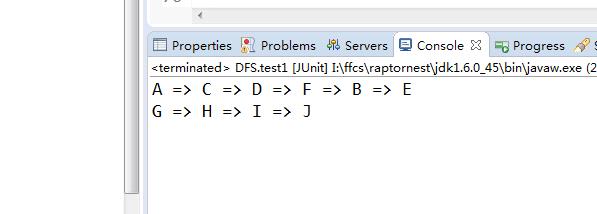
结果：