GIS算法原理与开发2021-深度优先遍历

Posted 2021-05-30 LLGISerlntu

图的遍历是GIS的网络数据结构中经常用到的算法，比如爆管后找到距离事故点最近的阀门，路径分析中寻找限定时间内最短时间与超限时条件下最低费用路径，配电网路径中搜索最佳路径算法等

图的遍历主要包含深度优先遍历和广度优先遍历

图的遍历是指从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程叫做图的遍历

深度优先遍历（Depth_First_Search）,也称为深度优先搜索，简称为DFS：就是从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发

深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到

算法原理

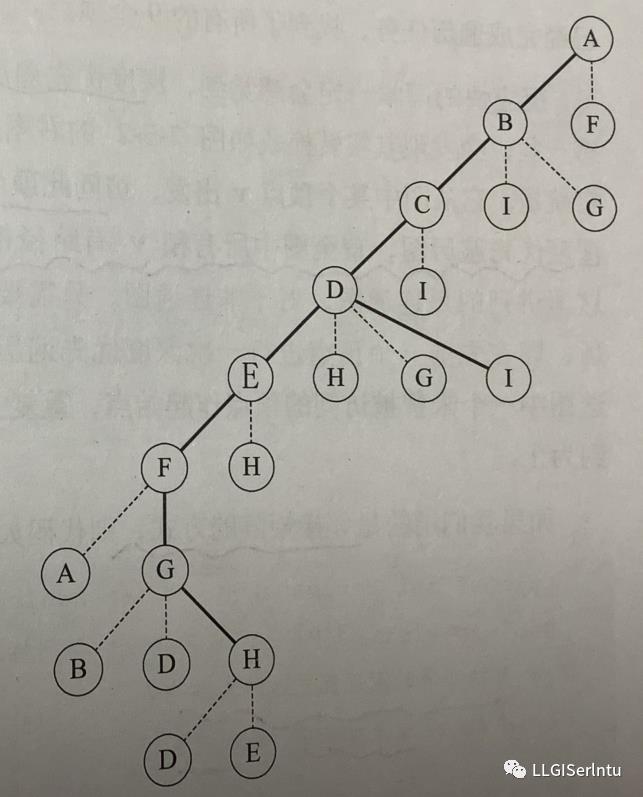
按照深度优先遍历，从A点出发，找到与A点连接的节点B和F，按照向右手边走的原则，确定下一节点为B，找到与B点连接的节点C，I，G，仍然按照右手原则，找到节点C，依次类推，直到找到F，按照右手原则找到A点，此时遍历完了一条连通路径，并将所有经过的点标记为已访问过；查找下一节点，从A点回退到F点找到未访问并与F连通的节点G点，依次类推，找到与G点连通但未访问的节点H，在H处再无通路，再次返回G点，无未访问的节点，再次返回到F，无未访问节点，返回到E，无未访问节点，再次返回到D，找到未访问节点I，与I相连的B和C都访问过了，再返回到C点，直到返回A点，遍历结束

A-B-C-D-E-F-A；

A-F-G-H

D-I

主要思想：先一条道跑到黑，然后从最后一个点每次回退一个节点，找到未访问的节点，直到最后回到初始节点，遍历完所有节点

图的存储

图由顶点和弧组成，所以我们可以将图抽象为邻接矩阵，用一维数组来存储顶点，用二维数组来表示边与边之间的邻接矩阵，如果二维数组的元素arr[1][3]为1表示点1和点3邻接，如果为0表示两个点不邻接

所以上图可表示为

arr1[9]={A,B,C,D,E,F,G,H,I}

arr2[0,0]=arr2[1,1]=arr2[2,2]=arr2[3,3]=arr2[4,4]=arr2[5,5]=arr2[6,6]=arr2[7,7]=arr2[8,8]=0;

arr2中其余的元素值都为1

以上图为例遍历算法的实现：

1）存储图的数据结构

2）按照右手原则找到一条完整的路径

3）从路径的最后一个节点开始执行回退操作

4）直到回到初始点，遍历完所有节点

调用深度优先遍历函数

 //定义 string[] str1 = { "A", "B", "C", "D", "E", "F", "G", "H","I" }; bool[] visited =new bool[9]; int[,] arr= new int[9, 9]; for(int i=0;i<9;i++) { for(int j=0;j<9;j++) { if (i==j) { arr[i, j] = 0; } else { arr[i, j] = 1; } } }
 //遍历 for (int i=0;i<str1.Length;i++) { if(visited[i]!=true) { string nodeid = str1[i]; int[] array = new int[9]; for (int m=0;m<9;m++) { array[m] = arr[i,m];
 }
 DFS(nodeid, visited, array, i); } }

遍历函数

 void DFS(string node,bool[] vis,int[] array,int j){ vis[j] = true;  Console.WriteLine(node + "----"); for(int i=0;i<array.Length;i++) { if (vis[i]!=true && array[i]!=1) {  DFS(node, vis, array, i); } } }

简单，下次应该改良下，多用些自定义类，自定义方法和函数，自定义数据结构......更加模块化些,让我的code体面一点

参考

1. 大话数据结构