求最近公共祖先(LCA)板子 x

Posted 2020-09-19 云深不知处

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了求最近公共祖先(LCA)板子 x相关的知识，希望对你有一定的参考价值。

LCA目前比较流行的算法主要有tarjian，倍增和树链剖分

1)tarjian

是一种离线算法，需要提前知道所有询问对

算法如下

　　1.读入所有询问对（u,v），并建好树（建议邻接表）

　　2.初始化每个节点各属一个并查集，都指向自己

　　3.对整棵树进行dfs（深度优先搜索）遍历

每处理到一个新节点(u)时看他的另一半（询问对象v）是否visit过，如果visit过了，则这组询问对的lca即v的并查集的根节点，若没有visit过，则继续向下深搜，该节点记为已visit

每当回溯的时候都将子节点的并查集并到父节点的并查集中

这样一遍走下来就完成了tarjian算法。

超详细tarjain:orz

2)树上倍增

f[i,j]表示i的第2^j祖先dfs预处理f[i,j]=f[f[i,j-1],j-1];

对于每一对x,y先将深度调成一样再枚举j逐一往上找，这两个过程都是log的

超详细树上倍增:orz

3)树剖

树剖(树链剖分)是一种在线算法，跑起来非常快，应该是目前LCA算法中最优的

建树后，我们需要把整棵树划为轻重链，

每一个非叶子节点都一定在一条重链上

定义：

重边：父节点与其子树最大（子节点最多）的节点的连边称为重边

轻边：非重边即为轻边

重链：相连的重边称为重链

划分重链后，我们要记一个jump数组表示存每个节点的“跳”的信息

如果这个节点在重链上，则jump[i]为它所属重链的根节点（最顶端）

如果这个节点不在重链上或者它是一条重链的顶端（根节点），那么jump[i]为它的父节点

接下来我们就可以处理询问对了

比如求两个节点a，b的LCA

我们先看他们是否在同一条重链上，如果是，则LCA即为深度较小的节点

如果不是，则我们需要比较jump[a]和jump[b]的深度，jump[a]比较浅则令a=jump[a]反之令b=jump[b]

重复以上过程直到a==b（LCA为这个节点）或a,b在同一条重链上时（LCA为深度浅的节点）

这样就完成了，复杂度虽说评是O(n*logn)但实际上跑起来快得多

超详细树剖:orz

练手题

洛谷 P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1：

输出样例#1：

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

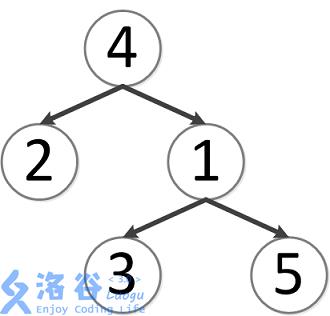
第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

LCA板子!!!

1)tarjan

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;

const int N = 500005;
const int M = 1000005;
int top,cnt,dad[N],ans[N];
bool used[N];

struct heads {
    int head;
}v1[N],v2[N];

struct Edge {
    int v,next,num;
}e1[M],e2[M];

void chu()
{
    memset(v1,-1,sizeof(v1));
    memset(v2,-1,sizeof(v2));
    memset(dad,-1,sizeof(dad));
    memset(used,0,sizeof(used));
}

int getdad(int x)
{return dad[x] == -1 ? x : dad[x] = getdad(dad[x]);}

void Unions(int a,int b)
{
    int r1=getdad(a);
    int r2=getdad(b);
    if(r1!=r2)
        dad[r2]=r1;
}

void add1(int u,int v)
{
    e1[top].v=v;
    e1[top].next=v1[u].head;
    v1[u].head=top++;
}

void add2(int u,int v,int i)
{
    e2[cnt].num=i;
    e2[cnt].v=v;
    e2[cnt].next=v2[u].head;
    v2[u].head=cnt++;
}

void Tarjan(int u)
{
    used[u]=true;
    for(int i=v1[u].head;i!=-1;i=e1[i].next)
    {
        int v=e1[i].v;
        if(used[v])
            continue;
        Tarjan(v);
        Unions(u,v);
    }
    int Ms;
    for(int i=v2[u].head;i!=-1;i=e2[i].next)
    {
        int v=e2[i].v;
        Ms=e2[i].num;
        if(used[v])///==getdad(v)
            ans[Ms]=getdad(v);
    }
}

int main()
{
    int n,m,s,u,v;
    scanf("%d%d%d",&n,&m,&s);
    chu();
    int nn=n;
    n--;
    while(n--)
    {
        scanf("%d%d",&u,&v);
        add1(u,v),add1(v,u);
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        add2(u,v,i),add2(v,u,i);
    }
    Tarjan(s);
    for(int i=1;i<=nn;i++)
        printf("%d\\n",ans[i]);
    return 0;
}

Tarjan版(无注释...)

2)树上倍增

#include <iostream>
#include <cstdio>
#include <cmath>
//maybe my English is not very good 

using namespace std;

const int M = 5e5 + 1;
int n,m,s;
int num; 
int deep[M],h[M];
bool vs[M];
int jumps[M][21];
int p;

struct A{
    int next;
    int to;
}t[M<<1];

inline int read() //optimize
{
    int x=0,f=1;char ch=getchar();

    while(ch<\'0\'||ch>\'9\')
    {
        if(ch==\'-\') f=-1;
        ch=getchar();
    }

    while(ch>=\'0\'&&ch<=\'9\')
    {
        x=x*10+ch-\'0\';
        ch=getchar();
    }

    return x*f;
}

void ADD(int x,int y) //connect the x and the y
{
    num++;
    t[num].to=y;
    t[num].next=h[x];
    h[x]=num;
}

void Dfs(int u)
{
    for(int i=h[u];i!=-1;i=t[i].next)
    {
        int v=t[i].to; //u\'s next side
        if(deep[v] == 0) //if v is not visited
        {
            deep[v]=deep[u]+1; //deep+1
            jumps[v][0]=u; //u is v\'s dad
            Dfs(v); //continue Dfs            
        }
    }
}

void steps()
{
    p=int(log(n)/log(2)+0.001); //find the biggest
    for(int i=1;i<=p;i++) //the Limit
        for(int j=1;j<=n;j++)
            jumps[j][i]=jumps[jumps[j][i-1]][i-1];
//the j jump 2^i can get to the (first jump 2^(i-1),then jump 2^i-1 can get to)
//eh...I will speak in Chinese.
//because 倍增 is use 次方的形式 increase
}

int LCA(int a,int b)
{
    //We let the b\'s deep is small
    if(deep[a]<deep[b]) swap(a,b);
    for(int i=p;i>=0;i--)
    {//first let the a jump to the b\'s deep
        if(deep[jumps[a][i]]>=deep[b])
        a=jumps[a][i];
    }
    if(a == b) return b; //if the b is them\'s LCA , return b
    for(int i=p;i>=0;i--) //jump together
    {
        if(jumps[a][i]!=jumps[b][i])
        a=jumps[a][i],b=jumps[b][i]; //update
    }
    return jumps[a][0]; 
}

int main()
{
    //s is the root
    n=read();m=read();s=read();
    for(int i=1;i<=n;i++) h[i]=-1;
    int x,y;
    for(int i=1;i<n;i++)
    {
        x=read();y=read();
        //connect the x and the y
        ADD(x,y);
        ADD(y,x);
    }
    deep[s]=1; //this is too important !!!
    //if you don\'t think so ,"//" it. 
    //and then you will know
    Dfs(s); //Dfs the root(s)
    steps(); //find the steps
    int a,b;
    while(m--)
    {
        a=read();b=read();
        printf("%d\\n",LCA(a,b));
    }
    return 0;
}

树上倍增英文版???

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<stdio.h>
#include<vector>
#define maxn 500500
using namespace std;
///隶属邻接表 
struct Edge{                    //邻接表的结构体 
    int from,to;
}edges[2*maxn];                 //边要乘2，因为是无向图 ； 
int first[maxn],next[2*maxn];   //同理； 
int read(){                        //读入优化，可以照着这个模板来写，这个还算写的比较好看。 
    int re=0;
    char ch=getchar();
    while (ch<\'0\' || ch>\'9\') ch=getchar();
    while (ch>=\'0\' && ch<=\'9\'){ 
        re=re*10+ch-\'0\'; 
        ch=getchar();
    }
    return re;
}
///////////////////////////////////////////////
///全局变量 
int n,m;
int root;
int height[maxn];
float log2n;
///////////////////////////////////////////////////////
///隶属LCA的全局变量 
int f[maxn][20];// 
int have[maxn];                           //have，有没有找过，这都是套路 。 
void dfs(int u,int h){                 //u代表点的标号，h代表高度。 
    int v;
    height[u]=h;
    for(int i=1;i<=log2n;i++) {
        if(h<=(1<<i)) break;              //由于i是从小到大计算的，故（1<<i）>=h 时可直接退出。请务必想清楚是<=  还是=。
        f[u][i] = f[ f[u][i-1] ][i-1]; //动规计算。同样也是一切倍增算法的核心。 
    }
    int k=first[u];
    while(k!=-1){
        v=edges[k].to;
        if(!have[v]) {
            have[v]=1;        
            f[v][0]=u;                 //将要找的下一个点的父节点标为当前处理的节点u。 
            dfs(v,h+1);
        }
        k=next[k];
    }
}
int require_LCA(int a,int b){
    int da=height[a],db=height[b];
//第一步，将a，b两点移到同样的高度，只动高度大的那个点而不动高度小的那个点。 
    if(da!=db) {
        if(da<db){                   //保证a的高度是大于b的高度的。 
            swap(a,b);
            swap(da,db);
        }
        int d=da-db;
        for(int i=0;i<=log2n;i++) 
            if( (1<<i) & d) a=f[a][i]; //这里的位运算可以减少代码量
                                       //考虑到d是一个定值，而（1<<i）在二进制中只有第（i+1）位是1； 
                                       //那么d与（1<<i）如果某一位为1，那么表示可以向上移动， 
                                       //如果此时不移动，那么i增大了后就无法使height[a]==height[b]了 
    }
//第二步,找到某个位置i，在这个位置时，f[a][i]!=f[b][i],但再向上移动一步，a，b相同了 
//从log2n开始从大到小枚举i，如果超过了a，b的高度，则令i继续减小
//如果没有超过a，b的高度，那么就判断移动了后会不会让a==b，
//是，则i继续减小，否则，令此时的a=f[a][i],b=f[b][i]; 
    if(a==b) return b;
    int i=0;
    for(i=log2n;i>=0;i--) {
        if(height[ f[a][i] ]<0) continue;
        if( f[a][i]==f[b][i] ) continue;
        else a=f[a][i],b=f[b][i];        //顺便一提，在第二步任何地方没有break；
                                       //我就是因为在这里写了一个break，然后找了我两个小时啊。 
    }    
    return f[a][0];
}
/////////////////////////////////
///据说从主函数开始阅读是个好习惯。 
int main(){
//    freopen("in2.txt","r",stdin);
    n=read();m=read();root=read();
    memset(first,-1,sizeof(first));
    memset(next,-1,sizeof(next));
    int s,t;
    int dsd=2*(n-1);
    for(int i=1;i<=dsd;i+=2) {
        s=read();t=read();      //读入优化。 
        edges[i].from=s;
        edges[i].to=t;
        edges[i+1].from=t;
        edges[i+1].to=s;
        next[i]=first[s];
        first[s]=i;
        next[i+1]=first[t];
        first[t]=i+1;
    }
    // 以上是邻接表，在此不再赘述。 
    log2n=log(n)/log(2)+1;        //C++计算log是自然对数，我们要用的以2为底的对数，故要除以log(2); 
                                  //对无理数加上1或是0.5是个好习惯，可以减小误差； 
    memset(have,0,sizeof(have));
    memset(height,0,sizeof(height));
    memset(f,-1,sizeof(f));
    have[root]=1;                //fa[][]和height[]要在dfs理进行计算，不然根本找不到某个非根节点的父亲是谁; 
    dfs(root,1);                
    for(int i=1;i<=n;i++){
        for(int j=0;j<=log2n;j++) {
            if(height[i] <=(1<<j) ) break;
        }
    }
    for(int i=0;i<m;i++) {      //应对要求进行求解。 
        s=read();t=read();
        int y=require_LCA(s,t);
        printf("%d\\n",y);
    }
    return 0;
}

中文版23333

3)树剖

#include <iostream>
#include <cstdio>
#define _(ch) ch=read()                    //便于读入 

using namespace std;

const int S = 500001;
bool f[S];                                 //dfs 标记
int n,m,s;
int fa[S];                                 //并查集 
int num,h[S];                             //邻接表 
int deep[S];                             //深度 
int sum[S];                             //子结点个数 
int dad[S];                             //链头元素 

struct B{
    int to,next;
}t[S<<1];

inline int read()                         //optimize
{
    int x=0,f=1;char ch=getchar();

    while(ch<\'0\'||ch>\'9\')
    {
        if(ch==\'-\') f=-1;
        ch=getchar();
    }

    while(ch>=\'0\'&&ch<=\'9\')
    {
        x=x*10+ch-\'0\';
        ch=getchar();
    }

    return x*f;  
}

void ADD(int x,int y)                     //connect the x and the y
{
    num++;
    t[num].to=y;
    t[num].next=h[x];
    h[x]=num;
}

inline int Find(int x)
//find the root (重链\'s top)
{return fa[x] == x ? x : fa[x] = Find(fa[x]);}

inline void Unions(int a,int b)
{                                        //union(搭重链)
    /*int f1=Find(a);
    int f2=Find(b);
    if(f1!=f2)
    {
        fa[f1]=f2;
    }*/
    fa[Find(b)]=Find(a);
}

inline void dfs(int p)//D is the (结点)
{//calc every D\'s son D
//每个结点的深度 
    f[p]=true;
    int maxx=0;                            //寻找子节点中拥有子结点个数最多的节点编号 
    sum[0]=-1;                            //0号没有子结点
    for(int j=h[p];j;j=t[j].next) 
    {                                    //进行遍历 
        int v=t[j].to;
        if(f[v]) continue;
        deep[v]=deep[p]+1;
        dad[v]=p;                        //p is v\'s dad 
        dfs(v);                         //continue dfs
        if(sum[v] > sum[maxx]) maxx=v;     //update
        sum[p]+=sum[v]+1;
//        p的子结点数 = p 的以\'v\'为根的子树的结点数目加上\'v\'这个点(即+1)
    }
    if(maxx) Unions(p,maxx);            //if updated 
    //that means find the (重链) succeed
}

inline int jump(int p)                     //find p can jump to  
{
    int top=Find(p);                     //(重链)\'s top 
    if(top == p) return dad[p];
//    如果p所处于的链的链头就是自己,也就是说,已经位于链的top处,所以只能够跳到他的父结点的位置,
//    所以直接return it\'s dad,即跳一步到达父结点处 
//    说白了就是说,一定要跳!!! 
    return top;                            //其余情况就返回链头就好(就是当前结点跳到了链头位置) 
}

inline int Lca(int a,int b)             //Lca 
{
    while(a!=b)                         //当两点不相等的时候就开始跳 
    {
        if(Find(a)==Find(b))             //如果它们位于同一条重链上 
          return deep[a]<deep[b] ? a:b; //直接返回深度较浅的那个点 
        int ja=jump(a),jb=jump(b);
        if(deep[ja] > deep[jb])            //如果a跳了之后没有到达b跳了之后的深度 
            a=ja;                        //就选取深度较深的点跳 
        else
            b=jb;
    }
    return a;
}

int main()
{
    _(n),_(m),_(s);
    int x,y;
    for(int i=1;i<n;i++)
    {
        _(x),_(y);
        ADD(x,y),ADD(y,x);
        fa[i]=i;                        //顺便初始化一下并查集 
    }
    fa[n]=n;                             //有一个没有进行初始化的并查集,进行初始化 
    deep[s]=1;                             //根结点的深度设置为1,非常重要!!!! 
    dfs(s);                                //寻找子节点个数,位于哪一条重链上 
    while(m--)
    {
        _(x),_(y);
        printf("%d\\n",Lca(x,y));
    }
    return 0;
}

混杂版(才不是英语不好！)

以上是关于求最近公共祖先(LCA)板子 x的主要内容，如果未能解决你的问题，请参考以下文章