P3379 模板最近公共祖先(LCA)
Posted sevenyuanluo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了P3379 模板最近公共祖先(LCA)相关的知识,希望对你有一定的参考价值。
www
LCA真的令人头大
(本蒟蒻用了一整个下午来理解加学习并且骚扰学长很久orz
LCA——least common ancestors (最近公共祖先
看一眼板子的题面吧
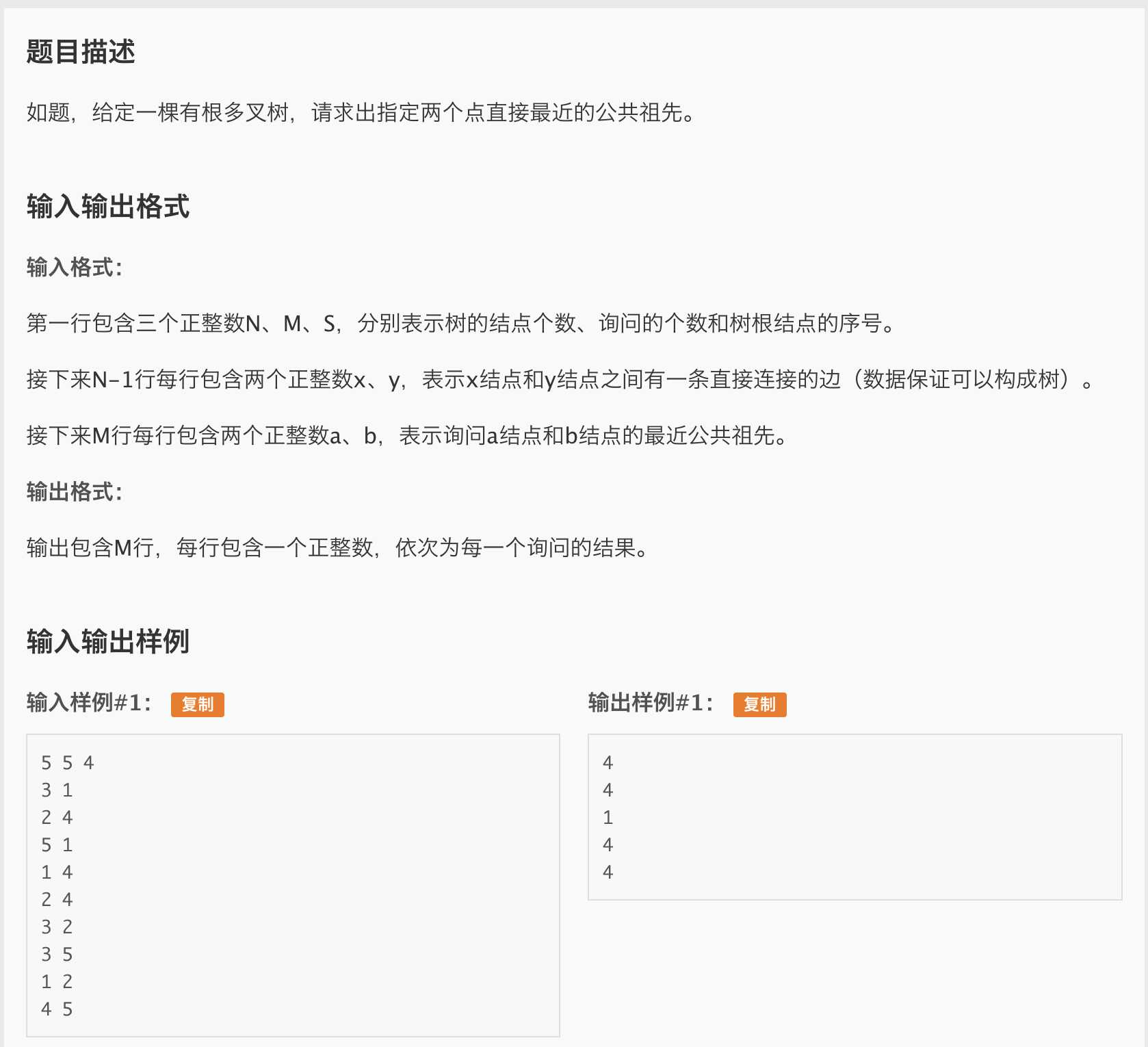
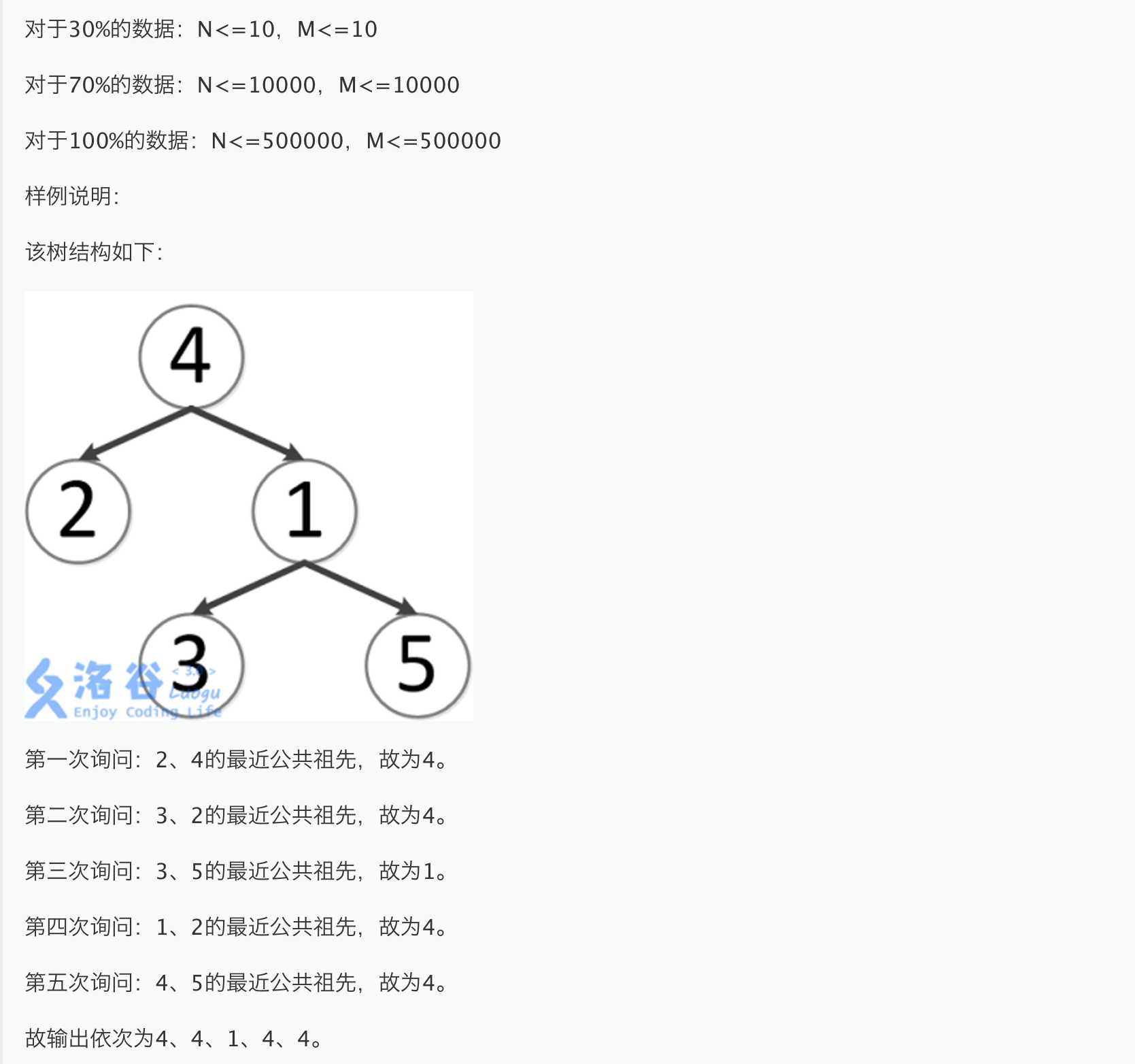
emmmmm样例说明很详细了吧,大概一下就能理解LCA是什么了
然后就开始代码实现
首先想到的一定是暴力算法
先建一棵树,再从询问的两个点向上搜,当两个点第一次搜到同一个父节点时,该点就是结果了
显然,会TLE
所以出现了倍增,每次跳1,2,4,8,16。。。。。。
这样可以大大提高效率,但是可能会出现一下子跳太远跳过的情况,所以应该从大往小跳
(除了倍增外还有其他算法然鹅我不会233333
看代码
#include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int maxn = 500010 * 2;//因为是无向图,边是双向的,数据范围要乘2 const int mlog = log2(500010) + 1;//跳的最大深度 struct edgee{ int nxt,to; }edge[maxn]; int head[maxn]; int depth[maxn]; int fa[maxn][30]; int cnt; void add(int x,int y){ edge[++cnt].to = y; edge[cnt].nxt = head[x]; head[x] = cnt; }//加边(链式向前星大概都会吧 void dfs(int x,int now){ depth[x] = now; for(int i = head[x];i;i = edge[i].nxt){ int v = edge[i].to; if(!depth[v]){ fa[v][0] = x; dfs(v,now + 1); } } }//递归计算每个点的深度(从根节点开始向下遍历 int LCA(int a,int b){ if(depth[a] < depth[b]) swap(a,b);//使a总为更深的点,便于操作 for(int j = mlog;j >= 0;j--) if(depth[a] - (1<<j) >= depth[b]) a = fa[a][j];//将a往下跳 if(a != b){ for(int j = mlog;j >= 0;j--){ if(fa[a][j] != fa[b][j]){ a = fa[a][j]; b = fa[b][j];//将a,b跳到同一深度 } } a = fa[a][0]; } return a;//返回节点编号 } int main(){ int n,m,s; scanf("%d%d%d",&n,&m,&s); for(int i = 1;i < n;i++){ int u,v; scanf("%d%d",&u,&v); add(u,v); add(v,u);//无向图,双向边 } dfs(s,1); for(int j = 1;j < mlog;j++) for(int i = 1;i <= n;i++) fa[i][j] = fa[fa[i][j - 1]][j - 1];//状态转移方程,画图辅助理解比较好,代表i节点的第j个父节点 for(int i = 1;i <= m;i++){ int a,b; scanf("%d%d",&a,&b); printf("%d ",LCA(a,b)); } return 0; }
虽然讲的不太好,但是加油鸭,您们肯定比我强,一定能理解
orz
以上是关于P3379 模板最近公共祖先(LCA)的主要内容,如果未能解决你的问题,请参考以下文章