MATLAB入门学习
Posted GraceSkyer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MATLAB入门学习相关的知识,希望对你有一定的参考价值。
背命令就行了。。。
线性代数
解线性方程组:
Ax=b
A是系数矩阵,x未知数,b是列向量
如果有唯一解,直接x=b\\A
第二 B=null(A,\'r\')求Ax=0的基础解系,B的列向量就是基础解系的列向量
C=null(A) 求出基础解系后将基础解系向量正交单位化存在C中
C=rref(A)求A的行最简形
结合之前学过的一些矩阵的命令比如rank,inv可以很好的解决线性方程组的问题。
怎么解线性方程组?先求Ax=0的基础解系,然后找Ax=b的一个特解。。。 ●▽●
然后,求特征值和特征向量
D=eig(A) 得到A的特征值
[Q,d]=eig(A) Q代表A的特征向量,d是对角矩阵,对角上的元素就是A的特征值
poly(A)求A 的特征多项式的系数
poly2str(poly(A),\'x\')这个可以显示多项式
orth(A)化为正交矩阵
然后没什么了。。。背吧背吧。。。╮(︶﹏︶")╭
微积分
首先介绍一下matlab里的符号计算
符号变量可以看成是数学中含参数 的表达式中的参数
也就是说matlab也是能进行像(a+b)(a-b)=a^2-b^2这样的计算的
要进行符号计算首先要定义符号变量
定义符号对象的命令是sym和syms
f=sym(s)表示把数字、字符串或者表达式s转化成符号变量f
然后syms可以将多个字符转化为符号变量
比如syms x y z;
这就是将x y z转化为符号变量
下面写个简单的例子(〃\'▽\'〃)~
syms a b
fab = (a + b)*(a - b)
下面介绍一些符号计算常用的命令~~~
collect 合并同类项
expand 展开表达式
factor 因式分解
numden 得到表达式的分子和分母
simplify 化简符号表达式
subs 将符号表达式的便令用其他符号或者数字代替
举一些例子:
具体的用法可以使用help命令查看~~~
下面开始微积分
第一部分:求极限
使用命令limit
这个的用法help写的简单明了
还可以求左右极限
第二部分:求积分
使用命令int
可以求定积分或不定积分
int(f,x)就是求不定积分
要求定积分在后面加一个区间就行了
比如int(f,x,0 ,1)
f也可以是含参变量的函数
int的第二个参数就是来指定被积的变量的
这是一个二重积分计算的例子:
第三部分:求微分
就是求导数啦~(*^__^*)
使用命令diff
diff(f,x,n)
对f关于x求n次导数
n=1的时候可以省略不写
第四部分:级数求和
使用命令symsum
s=symsum(an,n,a,b)
求Σan,n=a……b
无穷写作inf
另外一方面就是泰勒级数展开了,使用命令taylor
r=taylor(f,n,x,a)
求f在x=a处的n-1阶泰勒展开式,注意是n-1阶哦~ (^_−)☆
a不写的话默认为0 ,n不写的话默认为7
此外matlab还提供了泰勒技术逼近分析工具
输入taylortool即可打开这个工具进行使用,具体的还请自行研究,我不学了。。。✧(^_-✿
最后是解方程
这里就不仅限于线性方程
首先我们看看多项式求根~
在matlab里面一个行向量还可以表示一个多项式~~~
例如x^4-3*x^3+2*x-1
可以用向量表示为p=[1 -3 0 2 -1]
也就是将系数按照降幂排列写在向量里面
注意上面没有二次项要在对应的位置写上0不然会出错喔~
之后就可以用命令roots来求这个多项式的根
下面是代数方程(组)求解
用到的命令是solve
g = solve(eq) 对eq的默认变量进行求解
solve(eq,var) 对指定变量var求解
sovle(eq1,eq2,...,eqn) 对方程组eq1,2,...n,进行求解
下面举个例子:生成的结果是一个结构体s
还有最后一个命令fzero
fzero(fun,x) 可以求fun在x附近的零点。。。
那么微积分这一部分就讲完啦!!!
概率论与数理统计还没学完,统计功能我先不写了。。。其实简单的,也就是一些命令,要用查就行了嘛~
线性规划什么的,运筹学我也没学过,那先不学了。。。(((┏(; ̄▽ ̄)┛(逃
今天用MATLAB导入数据做分析来着,但好累啊不想写了。。。
目前我也没有时间更深入学习MATLAB了,要准备比赛和准备考试,感觉下个月要爆炸
..(。•ˇ‸ˇ•。)~o(>_<)o ~(ಥ﹏ಥ)。。宝宝要做个坚强的孩子!
入门就这样了。。完了完了。。。
看蓝猫学蓝猫,我有姿势我骄傲~~再见~~/(ㄒoㄒ)/~~
以上是关于MATLAB入门学习的主要内容,如果未能解决你的问题,请参考以下文章

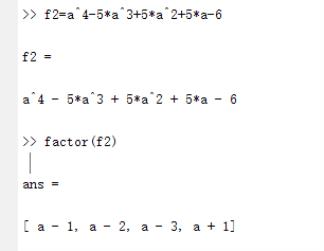



![]F)9%L(50(8CLA{~FA22~HY ]F)9%L(50(8CLA{~FA22~HY](https://image.cha138.com/20210609/5933bcc2b9144f159ff475e6d39b48c6.jpg)
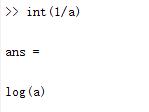

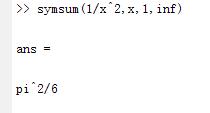
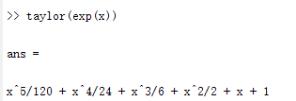
![}G}]09}@7HKNG6E54S))UWN }G}]09}@7HKNG6E54S))UWN](https://image.cha138.com/20210609/73a0d56dfd644c3bba341b19ac384037.jpg)
![()YX72J%GPL56]Q_UW{J(GK ()YX72J%GPL56]Q_UW{J(GK](https://image.cha138.com/20210609/2dc9ef9e8b6b48ed864f1f2e3a545548.jpg)
