LCS

Posted 2020-09-09 wqkant

LCS具有最优子结构

令 X=<x1,x2,...,xm> 和 Y=<y1,y2,...,yn> 为两个序列，Z=<z1,z2,z3,...,zk>为X和Y的任意LCS。则

如果xm=yn，则zk=xm=yn且Zk−1是Xm−1和Yn−1的一个LCS。 
如果xm≠yn，那么zk≠xm，意味着Z是Xm−1和Y的一个LCS。 
如果xm≠yn，那么zk≠yn，意味着Z是X和Yn−1的一个LCS。

  从上述的结论可以看出，两个序列的LCS问题包含两个序列的前缀的LCS，因此，LCS问题具有最优子结构性质。在设计递归算法时，不难看出递归算法具有子问题重叠的性质。 
  设C[i,j]表示Xi和Yj的最长公共子序列LCS的长度。如果i=0或j=0,即一个序列长度为0时，那么LCS的长度为0。根据LCS问题的最优子结构性质，可得如下公式：

 

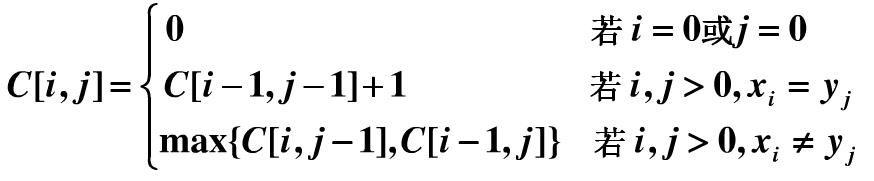
 代码实现

public class Main{
    static final int MAX=1000+1;
    private static final int C[][]=new int[MAX][MAX];
    private static final char B[][]=new char[MAX][MAX];
    private static int RecursiveLCS(char[] X,char Y[],int i,int j){
        if(i==0||j==0) return 0;
        if(C[i][j]>0) return C[i][j];
        if(X[i-1]==Y[j-1]){        
            C[i][j]=RecursiveLCS(X,Y,i-1,j-1)+1;
            
        }else{
            C[i][j]=Math.max(RecursiveLCS(X,Y,i-1,j),RecursiveLCS(X,Y,i,j-1));        
        }
        return C[i][j];
    }
    private static void LCS(char[] X,char Y[]){
        int XLen=X.length;
        int YLen=Y.length;
        for(int i=1;i<=XLen;i++){
            for(int j=1;j<=YLen;j++){
                if(X[i-1]==Y[j-1]){
                    C[i][j]=C[i-1][j-1]+1;
                    B[i][j]=\'↖\';
                }else if(C[i-1][j]>=C[i][j-1]){
                    C[i][j]=C[i-1][j];
                    B[i][j]=\'↑\';
                }else{
                    C[i][j]=C[i][j-1];
                    B[i][j]=\'←\';
                }
            }
        }
    }
//    private static void PrintLCS(char[] X,int i,int j){
//        if(i==0||j==0) return;
//        if(B[i][j]==\'↖\'){
//            PrintLCS(X,i-1,j-1);
//            System.out.print(X[i-1]);
//        }else if(B[i][j]==\'↑\'){
//            PrintLCS(X,i-1,j);
//        }else{
//            PrintLCS(X,i,j-1);
//        }
//    }
    private static void PrintLCS(char[] X,int i,int j){    
        int k=C[i][j];
        char [] S=new char[k];
        while(k>0){
            if(C[i][j]==C[i-1][j]){
                i--;
            }else if(C[i][j]==C[i][j-1]){
                j--;
            }else{
                S[--k]=X[i-1];
                i--;j--;
            }
        }
        System.out.println(S);
    }
    public static void main(String[] args){
        char [] X="ACCGGTCGAGTGCGCGGAAGCCGGCCGAA".toCharArray();
        char [] Y="GTCGTTCGGAATGCCGTTGCTCTGTAAA".toCharArray();
        RecursiveLCS(X,Y,X.length,Y.length);
        //LCS(X,Y);
        System.out.println(C[X.length][Y.length]);
        PrintLCS(X,X.length,Y.length);        
    }
}