经典问题LCS(最大公共子串问题)C代码实现
Posted createchance
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典问题LCS(最大公共子串问题)C代码实现相关的知识,希望对你有一定的参考价值。
LCS(Longest Commons Sequence)问题,也就是最长公共子串问题,是一个经典的算法问题。该问题在很多地方都会遇到。关于这个问题的解决方案,目前最佳的实现就是使用动态规划的方式进行实现,关于使用动态规划设计这个问题算法的过程,这里就不再描述了,网上有很多的描述,整理如下:
wiki百科中的描述:https://en.wikipedia.org/wiki/Longest_common_subsequence_problem
UCI的《算法导论》课程线上教案:https://www.ics.uci.edu/~eppstein/161/960229.html
国立清华大学(台湾)线上教案:http://www.csie.ntnu.edu.tw/~u91029/LongestCommonSubsequence.html
等等,线上的资料太多了,我就不再重复造车轮了,建议大家吧前面几个链接中的资料好好看一下。下面是北京大学曲婉玲教授等编写的《算法设计与分析》第二版中的LCS描述截图:



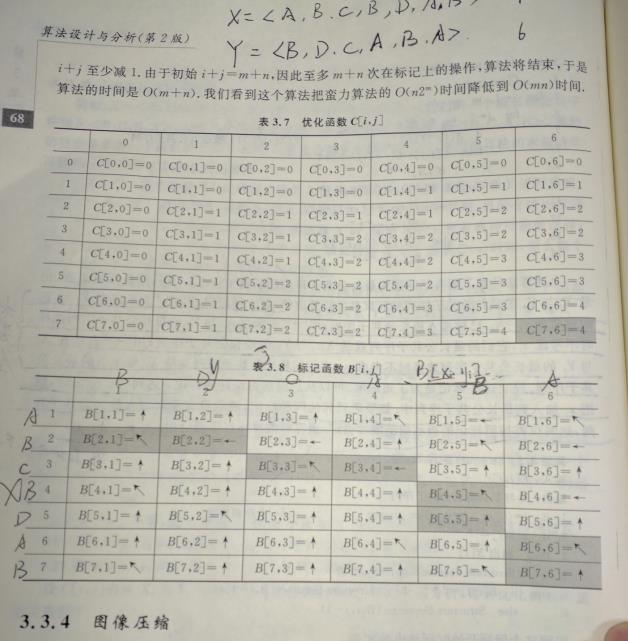
下面我给出一个使用C语言实现的LCS,使用上图中的伪代码方法:
/*************************************************************************
> File Name: lcs.c
> Author: Baniel Gao
> Mail: createchance@163.com
> Created Time: Tue 29 Nov 2016 01:53:13 PM CST
************************************************************************/
#include <stdio.h>
#include <string.h>
// 追踪标记
// 这里的实现不是很好,但是C语言二维数据指针操作真是的很恶心,所以出此下策
char tracker[100][100];
void print_lcs_by_tracker(char* str1, int m, int n)
if (m == 0 || n == 0)
return;
if (tracker[m - 1][n - 1] == '\\\\')
print_lcs_by_tracker(str1, m - 1, n - 1);
printf("%c", str1[m - 1]);
else if(tracker[m - 1][n - 1] == '|')
print_lcs_by_tracker(str1, m - 1, n);
else
print_lcs_by_tracker(str1, m, n - 1);
void lcs(char* str1, char* str2, int m, int n)
int len = 0;
int len_arr[m + 1][n + 1];
for (int i = 0; i <= m; i++)
len_arr[i][0] = 0;
for (int i = 0; i <= n; i++)
len_arr[0][i] = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (str1[i] == str2[j])
len_arr[i + 1][j + 1] = len_arr[i][j] + 1;
tracker[i][j] = '\\\\';
else if (len_arr[i][j + 1] >= len_arr[i + 1][j])
len_arr[i + 1][j + 1] = len_arr[i][j + 1];
tracker[i][j] = '|';
else
len_arr[i + 1][j + 1] = len_arr[i + 1][j];
tracker[i][j] = '-';
printf("Length array is: \\n");
for (int i = 0; i <= n; i++)
printf("\\t%d", i);
printf("\\n");
for (int i = 0; i <= n; i++)
printf("\\t___", i);
printf("\\n");
for (int i = 0; i <= m; i++)
printf("%d\\t|", i);
for (int j = 0; j <= n; j++)
printf("%d\\t", len_arr[i][j]);
printf("\\n");
printf("Tracker is: \\n");
for (int i = 1; i <= n; i++)
printf("\\t%d", i);
printf("\\n");
for (int i = 1; i <= n; i++)
printf("\\t___", i);
printf("\\n");
for (int i = 0; i < m; i++)
printf("%d\\t|", i + 1);
for (int j = 0; j < n; j++)
printf("%c\\t", tracker[i][j]);
printf("\\n");
printf("Len of LCS is: %d. \\n", len_arr[m][n]);
printf("LCS is: ");
print_lcs_by_tracker(str1, m, n);
printf("\\n");
int main(int argc, char *argv[])
int lcs_len = 0;
if (argc != 3)
printf("Usage: %s <string1> <string2> \\n", argv[0]);
return -1;
char* x = argv[1];
char* y = argv[2];
int m = strlen(x);
int n = strlen(y);
lcs(x, y, m, n);
return 0;
运行截图:
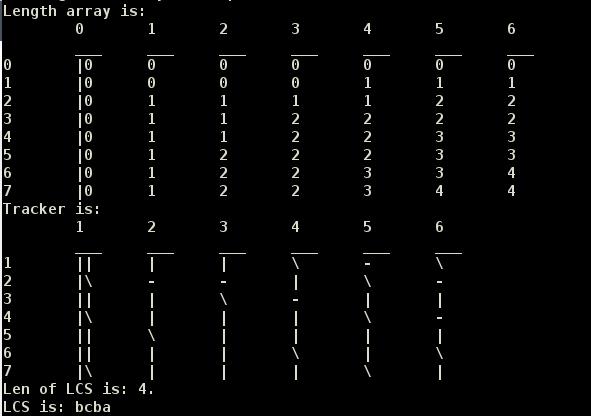
以上是关于经典问题LCS(最大公共子串问题)C代码实现的主要内容,如果未能解决你的问题,请参考以下文章