基于接缝裁剪的图像压缩 算法导论
Posted lineaar
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于接缝裁剪的图像压缩 算法导论相关的知识,希望对你有一定的参考价值。
给定一副彩色图像,它由一个mxn的像素数组A[1..m,1..n]构成,每个像素是一个红绿蓝(RGB)亮度的三元组。假定我们希望轻度压缩这幅图像。具体地,我们希望从每一行中删除一个像素,使得图像变窄一个像素。但为了避免影响视觉效果,我们要求相邻两行中删除的像素必须位于同一列或相邻列。也就是说,删除的像素构成从顶端行到底端行的一条“接缝”(seam),相邻像素均在垂直或对角线方向上相邻。
a.证明:可能的接缝数量是m的指数函数,假定n>1.
第1行有n种可能选取像素点方式,第2到m行中每行有2-3种(可能选中A[i][j-1],A[i][j],A[i][j+1]. (j=1 or j=n时,是2种可能)),所以总共有至少大于n*2^(m-1).
b 假定现在对每个像素A[i,j]我们都已计算出一个实型的“破坏度”d[i,j],表示删除像素A[i,j]对图像可视效果的破坏程度。直观地,一个像素的破坏度越低,它与相邻像素的相似度越高。再假定一条接缝的破坏度定义为包含的响度的破坏度之和。设计算法,寻找破坏度最低的接缝。分析算法的时间复杂度。
求破坏度最低的接缝很简单,c[i,j]记录接缝走到当前像素的最低破坏度。从第一行开始,c[i,j]只有当前像素的破坏度,直接赋值即可;第i行,每个像素的上一个像素来源一共有三个,左上、正上和右上方,每次计算c[i,j]时,需要去三种情况中破坏度最低的情况然后加上当前像素的破坏度,就是接缝走到当前像素的最低破坏度。递推式为c[i][j]=d[i][j]+min{c[i-1][j-1],c[i-1][j],c[i-1][j+1]}。
参考链接:http://www.ithao123.cn/content-6605545.html
// 15-8.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include<iostream> #include<time.h> #define ROW 10 #define COL 10 #define Left -1 #define Center 0 #define Right 1 #define INF 65536 using namespace std; int c[ROW + 1][COL + 2]; int r[ROW + 1][COL + 1]; int maxj; void carving(int d[][COL + 1]) { //给第0,1行赋值 for (int j = 0; j <= COL; j++) { c[0][j] = 0; r[0][j] = Center; c[1][j] = d[1][j]; r[1][j] = Center; } //给边界0,COL赋值做哨兵,由此在下面求C[i][j]时不用检查j是否为0或COL; for (int i = 0; i <= ROW; i++) { c[i][0] = INF; c[i][COL + 1] = INF; } //根据递归式求c[i][j],从第二行开始 for(int i=2;i<=ROW;i++) for (int j = 1; j <= COL; j++) { int temp = INF; for (int k = j - 1; k <= j + 1; k++) { if (c[i - 1][k] < temp) { temp = c[i - 1][k]; r[i][j] = k - j; } } c[i][j] = temp+d[i][j]; } //求最后一行最小的值就是最小的裁剪代价 int temp = INF; for (int j = 1; j <= COL; j++) if (c[ROW][j] < temp) { temp = c[ROW][j]; maxj = j; } //打印出c[i][j] cout << "c[i][j]:\\n" << "最小的切缝代价为" << temp << endl; for (int i = 1; i <= ROW; i++) { for (int j = 1; j <= COL; j++) cout << c[i][j] << \'\\t\'; cout << endl; } } //因为从最后一行回推出路径,因此用递归来打印 void display(int row,int maxj) { switch (r[row][maxj]) { case -1:display(row - 1, maxj - 1); cout << "\\\\" << endl; break; case 0: display(row - 1, maxj); cout << "||" << endl; break; case 1:display(row - 1, maxj + 1); cout << "//" << endl; break; } } int main() { //用5-15随机数初始化d[i][j]; srand((int)time(0)); //产生随机数种子 int d[ROW + 1][COL + 1]; for (int i = 0; i <= ROW; i++) for (int j = 0; j <= COL; j++) d[i][j] = 5 + rand() % 10; cout << "d[i][j]:\\n"; for (int i = 1; i <= ROW; i++) { for (int j = 1; j <= COL; j++) cout << d[i][j] << \'\\t\'; cout << endl; } cout << "----------------------------------------------------------------------------" << endl; carving(d); cout << "----------------------------------------------------------------------------" << endl; display(ROW, maxj); while (1); return 0; }
结果如下图所示:
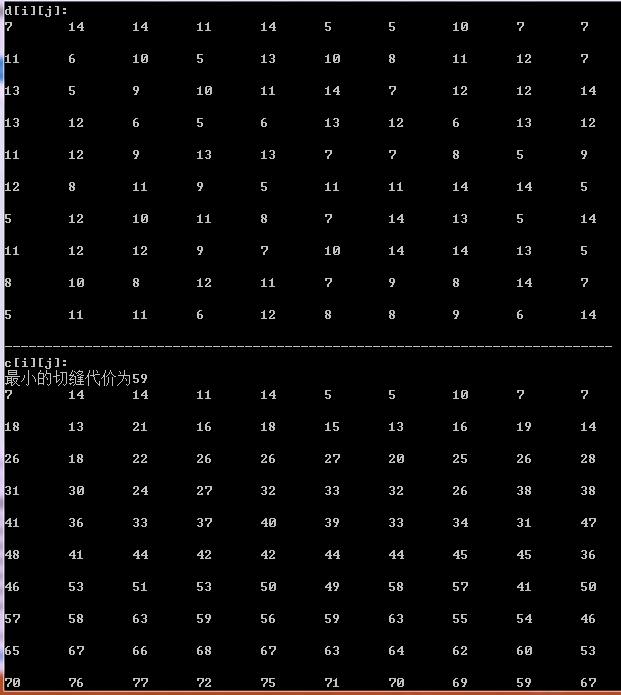
以上是关于基于接缝裁剪的图像压缩 算法导论的主要内容,如果未能解决你的问题,请参考以下文章