八大排序算法

Posted 2020-09-03

1:插入排序 - 直接插入排序

---

基本思想:

　　将一个数字插入到已排好序的有序表当中,从而得到一个新的更大的有序表, 即将序列的第一个记录看成是一个有序的子序列, 然后将从第二个记录插入, 直至整个序列都有序为止.

　　如果发现一个和插入元素相等的,我们既可以将元素按照原来的顺序摆放得到稳定排序, 也可以改变位置得到不稳定排序.

　　算法实现:   效率 O(n^2)

    void print(int a[], int n ,int i){  
        cout<<i <<":";  
        for(int j= 0; j<8; j++){  
            cout<<a[j] <<" ";  
        }  
        cout<<endl;  
    }  
      
      
    void InsertSort(int a[], int n)  
    {  
        for(int i= 1; i<n; i++){  
            if(a[i] < a[i-1]){               //若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入  
                int j= i-1;   
                int x = a[i];        //复制为哨兵，即存储待排序元素  
                a[i] = a[i-1];           //先后移一个元素  
                while(x < a[j]){  //查找在有序表的插入位置  
                    a[j+1] = a[j];  
                    j--;         //元素后移  
                }  
                a[j+1] = x;      //插入到正确位置  
            }  
            print(a,n,i);           //打印每趟排序的结果  
        }  
          
    }  
      
    int main(){  
        int a[8] = {3,1,5,7,2,4,9,6};  
        InsertSort(a,8);  
        print(a,8,8);  
    }  

 

 2:插入排序 -希尔排序(Shell\'s Sort)

---

　　希尔排序于1959年由D.L.Shell提出,相对于直接排序有较大的改进.希尔排序又称为缩小量排序.

基本思想:

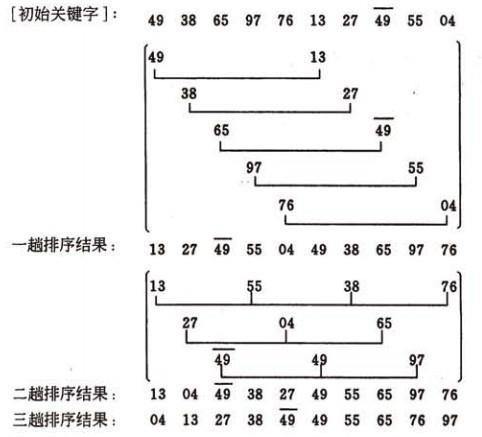
　　将整个待排序的记录序列分割成若干子序列分别进行直接插入排序, 待整个序列中的记录基本有序的时候, 再对全体记录进行依次直接插入排序.

操作方法:

　　1:选择一个增量序列t1,t2,t3,...,tk,其中ti>tj, tk=1;

　　2:按增量序列的个数k, 对序列进行k趟排序.

　　3:每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m的子序列,分别对各个子表进行直接插入排序, 仅增量因子位1 时, 整个序列作为一个表来处理, 表长度位整个序列的长度.

算法实现:

void shellsort(int a[], int n)
{
    int i, j, gap;

    for (gap = n / 2; gap > 0; gap /= 2) //gap4
        for (i = gap; i < n; i++)           //从4开始增加
            for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap) //
                swap(a[j], a[j + gap]);
}

 

 3:选择排序 - 简单选择排序(Simple Selection Sort)

---

基本思想:

　　在要排序的一组数中,选出最小(最大也可以)的数组,和第一个数进行交换, 在剩下的数中选出第二小的和第二个数字进行交换,以此类推.

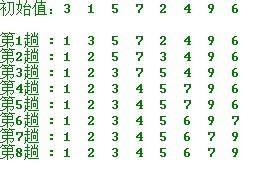
操作方法:

　　略

实现算法:

void SelectionSort(int a[],int n)
{
    int pos = 0,minPos = INT_MAX,selPos = 0,i;// 从 0 点开始
    for(;selPos<n;selPos++) // 从第一个位置开始排序.
    {
        for(i=selPos,minPos = INT_MAX;i<n;i++) // 找到目前最小数的坐标
        {
            if(a[i] < minPos)
            {
                pos = i;
                minPos = a[i];
            }
        }
        swap(a[pos],a[selPos]);
    }

}

 

4:选择排序 - 堆排序

---

 

 　　堆排序是一种树型选择排序,是对直接选择排序的有效改进.

基本思想:

　　具有N个元素的序列(k1,k2,k3.......kn),当且仅当满足

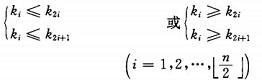
　　 时称为堆,由堆的定义可以看出,堆顶元素(即第一个元素)必须为最小项(小顶堆)

　　若用一维数组储存一个堆,则堆对应一颗完全二叉树,且所有非叶结点的值均不大于其子女的值.

　　(a) 大顶堆序列:(96,83,27,38,11,09)

　　(b) 小顶堆序列:(12,36,24,85,47,30,53,91)

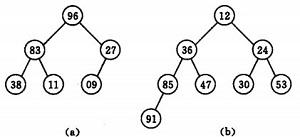
　　初始时要把排序的n个数的序列看做是一颗顺序储存的二叉树(一维数组储存的二叉树), 调整他们的储存顺序,使之成为一个堆, 讲堆顶元素输出,得到n个元素中的最小或者最大的元素, 这是堆的根节点的的数量最小或者最大,然后堆前面的(n-1)个节点重新调整使之称为新的堆,输出对应元素,得带n个元素中次大或者次小的元素. 以此类推,直到只有两个节点的堆.

　　因此我们就有了另一个问题(有点像,我觉得这个问题正则表达式可以解决,所以我现在有两个问题了.):

　　　　1: 如何将n个待排序的数字建成堆.

　　　　2: 输出堆顶元素之后, 怎样调整剩余的n-1个元素, 使其成为一个新堆 . 

　　1) 首先讨论第二个问题: 输出堆顶元素之后, 对剩余的m-1 个元素,讲话堆低元素送入堆顶, 堆被破坏, 其原因是根节点不满足堆得性质.

　　2) 将根节点和左右子树中较小元素进行交换.

　　3) 若与左子树交换: 如果左子树的堆被破坏, 即左子树的根节点不满足堆的性质, 则重复方法2.

　　4) 若与右子树交换: 如果右子树的堆被破坏, 即右子树的根节点不满足堆得性质, 则重复方法2.

　　5) 继续对不满足堆性质的子树进行上述操作, 直到叶子节点, 堆被建成. 

　　　　　　　　称这个自根节点到叶子节点的调整过程称为筛选. 如图所示:

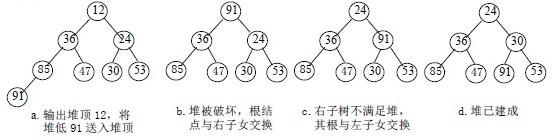
　　现在讨论如何将一些数字建立为一个初始化的堆.

　　1) n个节点的完全二叉树, 最后一个节点是第[n/2] 个节点的子树.

　　2) 筛选从筛选从第[n/2] 个节点的子树开始, 该子树成为堆.

　　3) 之后向前依次对各个节点为根的子树进行筛选使之称为堆, 直至根节点.

如图所示为 建堆过程: 无序序列:  (49，38，65，97，76，13，27，49)

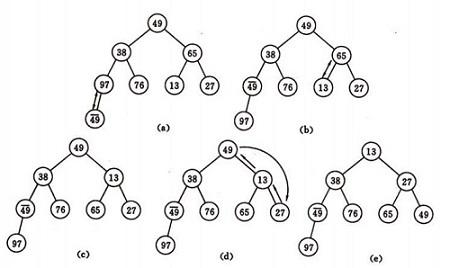
　　从算法描述上来看, 堆排序需要两个过程 一: 建立堆 , 二 : 堆顶和堆的最后一个元素交换位置. 所以堆排序需要两个函数, 一是堆的渗透函数 , 二是 饭后服调用渗透函数实现排序的函数 .

算法的实现:

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<limits.h>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<string>
#include<sstream>
#include<map>
#include<cctype>
using namespace std;
void print(int a[], int n){
    for(int j= 0; j<n; j++){
        cout<<a[j] <<"  ";
    }
    cout<<endl;
}



/**
 * 已知H[s…m]除了H[s] 外均满足堆的定义
 * 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选,
 *
 * @param H是待调整的堆数组
 * @param s是待调整的数组元素的位置
 * @param length是数组的长度
 *
 */
void HeapAdjust(int H[],int s, int length)
{
    int tmp  = H[s];
    int child = 2*s+1; //左儿子的位置
    while (child < length)
    {
        if(child+1 <length && H[child]<H[child+1])
        { // 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)
            ++child ;
        }
        if(H[s]<H[child])
        {  // 如果较大的子结点大于父结点
            H[s] = H[child]; // 那么把较大的子结点往上移动，替换它的父结点
            s = child;         // 重新设置s ,即待调整的下一个结点的位置
            child = 2*s+1;
        }
        else
        {             // 如果当前待调整结点大于它的左右孩子，则不需要调整，直接退出
             break;
        }
        H[s] = tmp;            // 当前待调整的结点放到比其大的孩子结点位置上
    }
    print(H,length);
}


/**
 * 初始堆进行调整
 * 将H[0..length-1]建成堆
 * 调整完之后第一个元素是序列的最小的元素
 */
void BuildingHeap(int H[], int length)      //  开始建堆
{
    //最后一个有孩子的节点的位置 i=  (length -1) / 2
    for (int i = (length -1) / 2 ; i >= 0; --i)
        HeapAdjust(H,i,length);
}
/**
 * 堆排序算法
 */
void HeapSort(int H[],int length)
{
    //初始堆
    BuildingHeap(H, length);
    //从最后一个元素开始对序列进行调整
    for (int i = length - 1; i > 0; --i)
    {
        //交换堆顶元素H[0]和堆中最后一个元素
        int temp = H[i]; H[i] = H[0]; H[0] = temp;
        //每次交换堆顶元素和堆中最后一个元素之后，都要对堆进行调整
        HeapAdjust(H,0,i);
  }
}

int main(){
    int H[10] = {3,1,5,7,2,4,9,6,10,8};
    cout<<"初始值：";
    print(H,10);
    HeapSort(H,10);
    //selectSort(a, 8);
    cout<<"结果：";
    print(H,10);

}

 

5: 交换排序 - 冒泡排序(Bubble Sort)

基本思想:

　　在要排序的一组数中,对当前还未排好序的范围内的全部数, 自上而下堆相邻的相隔数进行一次比较和调整让最大的数下沉, 小的数上升.

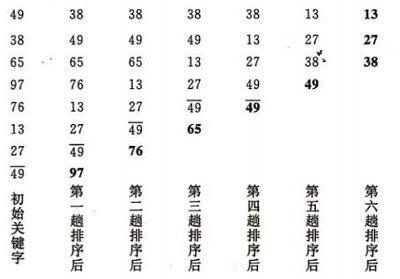
void bubbleSort(int a[], int n){
    for(int i =0 ; i< n-1; ++i) {
        for(int j = 0; j < n-i-1; ++j) {
            if(a[j] > a[j+1])
            {
                int tmp = a[j] ; a[j] = a[j+1] ;  a[j+1] = tmp;
            }
        }
    }
}

6: 交换排序 - 快速排序(Quick Sort)

基本思想:

　　1) 选择一个基准元素, 通常选择第一个元素,或者最后一个元素.

　　2) 通过一趟排序将待排序列分为独立的两部分, 其中一部分的记录的元素值 均比基准元素小 . 而另一部分记录的元素值 比基准值大

　　3) 此时基准元素在其排好序之后的正确位置.

　　4) 然后堆这两部分记录用同样的方法进行排序, 直至序列有序.

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<limits.h>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<string>
#include<sstream>
#include<map>
#include<cctype>
using namespace std;
void print(int a[], int n){
    for(int j= 0; j<n; j++){
        cout<<a[j] <<"  ";
    }
    cout<<endl;
}

void swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

int partition(int a[], int low, int high)
{
    int privotKey = a[low];                    //基准元素
    while(low < high){                    //从表的两端交替地向中间扫描
        while(low < high  && a[high] >= privotKey) --high; //从high 所指位置向前搜索，至多到low+1 位置。将比基准元素小的交换到低端
        swap(&a[low], &a[high]);
        while(low < high  && a[low] <= privotKey ) ++low;
        swap(&a[low], &a[high]);
    }
    print(a,10);
    cout<<"---"<<low<<"-----"<<"------"<<high<<endl;
    return low;
}


void qsort_improve(int r[ ],int low,int high, int k){
    if( high -low > k ) { //长度大于k时递归, k为指定的数
        int pivot = partition(r, low, high); // 调用的Partition算法保持不变
        qsort_improve(r, low, pivot - 1,k);
        qsort_improve(r, pivot + 1, high,k);
    }
}
void quickSort(int r[], int n, int k){
    qsort_improve(r,0,n,k);//先调用改进算法Qsort使之基本有序

    //再用插入排序对基本有序序列排序
    for(int i=1; i<=n;i ++){
        int tmp = r[i];
        int j=i-1;
        while(tmp < r[j]){
            r[j+1]=r[j]; j=j-1;
        }
        r[j+1] = tmp;
    }

}



int main(){
    int a[10] = {3,1,5,7,2,4,9,6,10,8};
    cout<<"初始值：";
    print(a,10);
    quickSort(a,9,4);
    cout<<"结果：";
    print(a,10);

}

7: 归并排序 (Merge Sort)

基本思想:

　　归并排序是将两个(或者两个以上)的有序表合成一个新的有序表, 即将待排序的序列分成若干个子序列, 每个子序列是有序的. 然后再把有序子序列合并成整体有序序列.

 

 

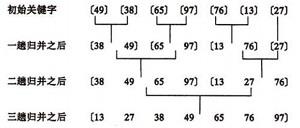
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<limits.h>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<string>
#include<sstream>
#include<map>
#include<cctype>
using namespace std;

/*合并arr的左右两部分： arr[l..m] 和 arr[m+1..r]  */
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 =  r - m;

    /* create temp arrays */
    int L[n1], R[n2];

    /* 复制数据到 L[] 和 R[] */
    for(i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for(j = 0; j <= n2; j++)
        R[j] = arr[m + 1+ j];

    /* 将两部分再合并到 arr[l..r]*/
    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2)
    {
        if (L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    /* 复制剩下的部分 L[] */
    while (i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }

    /* 复制剩下的部分 R[] */
    while (j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }
}

/* 对数据arr排序，从l到r */
void mergeSort(int arr[], int l, int r)
{
    if (l < r)
    {
        int m = l+(r-l)/2; //和 (l+r)/2 一样, 但是可以避免溢出在 l 和 r较大时
        mergeSort(arr, l, m);
        mergeSort(arr, m+1, r);
        merge(arr, l, m, r);
    }
}

void printArray(int A[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", A[i]);
    printf("\\n");
}

/*测试程序 */
int main()
{
    int arr[] = {12, 11, 13, 5, 6, 7};
    int arr_size = sizeof(arr)/sizeof(arr[0]);

    printf("Given array is \\n");
    printArray(arr, arr_size);

    mergeSort(arr, 0, arr_size - 1);

    printf("\\nSorted array is \\n");
    printArray(arr, arr_size);
    return 0;
}