数据结构初阶第九篇——八大经典排序算法总结(图解+动图演示+代码实现+八大排序比较)
Posted 呆呆兽学编程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构初阶第九篇——八大经典排序算法总结(图解+动图演示+代码实现+八大排序比较)相关的知识,希望对你有一定的参考价值。
⭐️本篇博客我要来和大家一起聊一聊数据结构初阶中的最后一篇博客——八大经典排序算法的总结,其中会介绍他们的原来,还有复杂度的分析以及各种优化。
⭐️博客代码已上传至gitee:https://gitee.com/byte-binxin/data-structure/tree/master/Sort2.0
目录
🌏排序总览
🍯什么是排序?
🍤 我们可以先了解一下两个概念:
🍤 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
🍤 排序的稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
🍯为什么要排序?(作用)
💿排序的在生活中应用十分广泛,比如在我们刷抖音短视频的时候,大数据根据我们的喜好,会把我们喜欢的推送给我们,还有我们购物可以根据价格升降序之类的来选择商品等等。
💿所以说排序真的是十分的重要。
🍯排序的分类
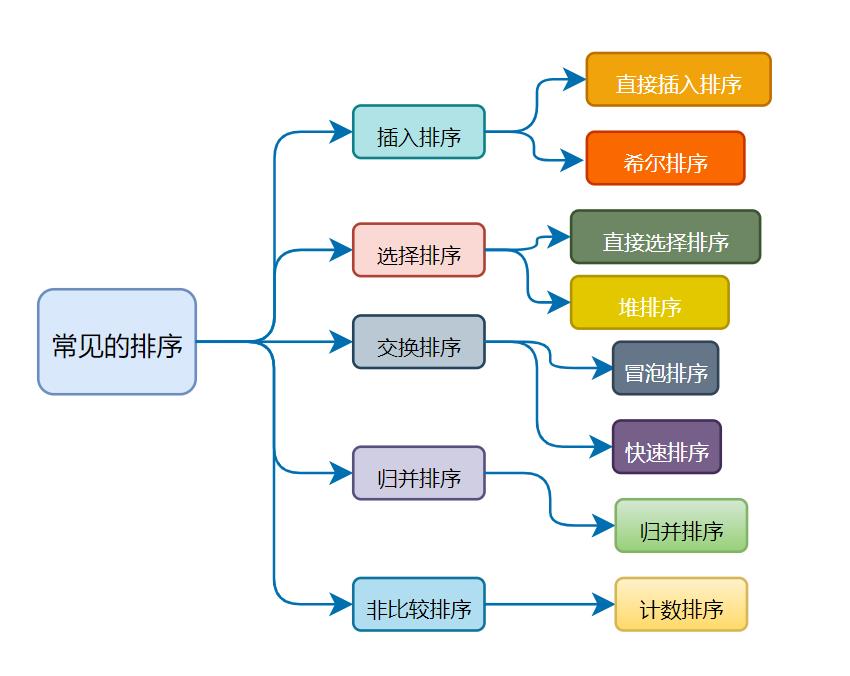
🌏插入排序
🌴直接插入排序
🍇基本思想:把待排序的数逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
🍇一般地,我们把第一个看作是有序的,所以我们可以从第二个数开始往前插入,使得前两个数是有序的,然后将第三个数插入直到最后一个数插入。
我们可以先看一个动图演示来理解一下:
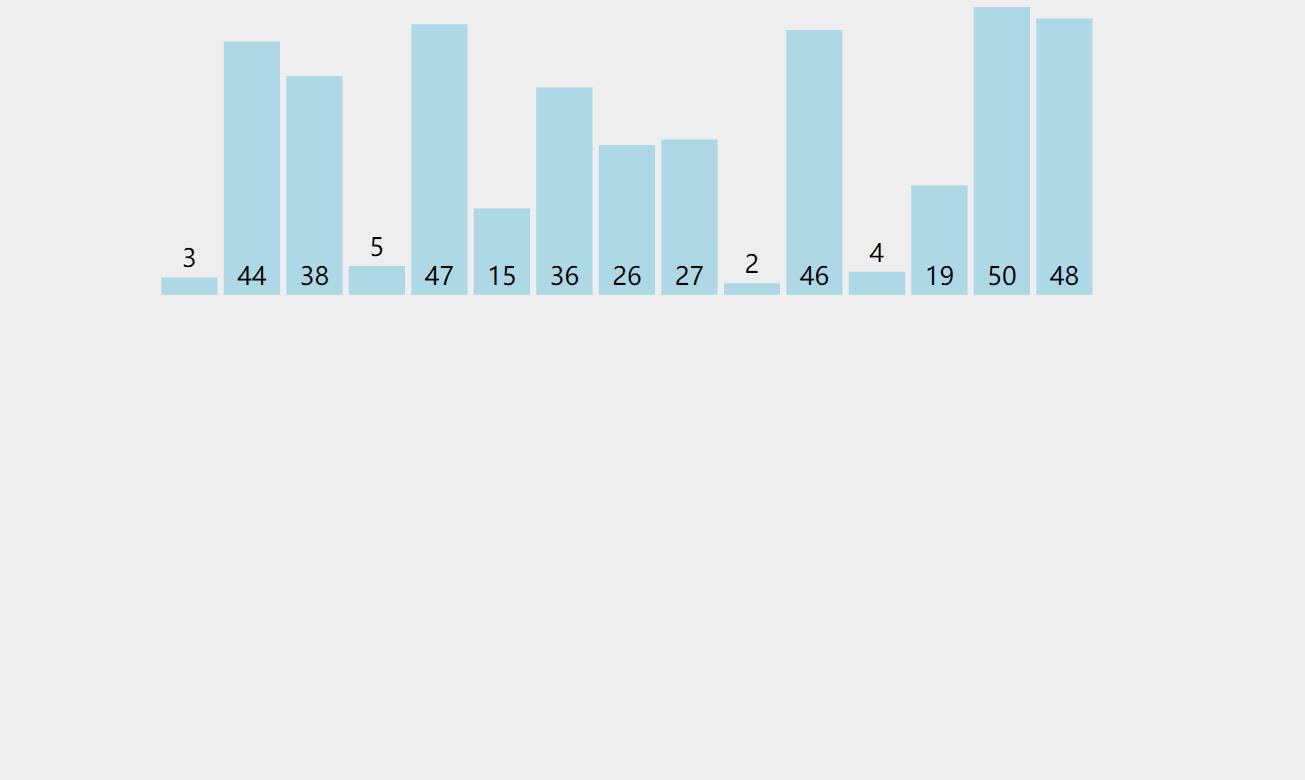
为了让大家更好地理解代码是怎么实现的,我们可以实现单趟的排序,代码如下:
int end = n-1;
// 先定义一个变量将要插入的数保存起来
int x = a[end + 1];
while (end >= 0)
// 直到后面的数比前一个数大时就不往前移动,就直接把这个数放在end的后面
if (a[end] > x)
a[end + 1] = a[end];
end--;
else
break;
a[end + 1] = x;
🍇前面我们也说了,是从第二个是开始往前插入,所以说第一趟的end应该为0,最后一趟的end应该是end = n - 2,根据end+1<n可以推出。
所以直接插入排序的整个过程的代码实现如下:
void InsertSort(int* a, int n)
int i = 0;
for (i = 0; i < n - 1; i++)
int end = i;
// 先定义一个变量将要插入的数保存起来
int x = a[end + 1];
// 直到后面的数比前一个数大时就不往前移动,就直接把这个数放在end的后面
while (end >= 0)
if (a[end] > x)
a[end + 1] = a[end];
end--;
else
break;
a[end + 1] = x;
🍇时间复杂度和空间复杂度的分析
时间复杂度: 第一趟end最多往前移动1次,第二趟是2次……第n-1趟是n-1次,所以总次数是1+2+3+……+n-1=n*(n-1)/2,所以说时间复杂度是O(n^2)
最好的情况: 顺序
最坏的情况: 逆序
:给大家看一下直接插入排序排100w个数据要跑多久
空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
🍇直接插入排序稳定性的分析
直接插入排序在遇到相同的数时,可以就放在这个数的后面,就可以保持稳定性了,所以说这个排序是稳定的。
🌴希尔排序
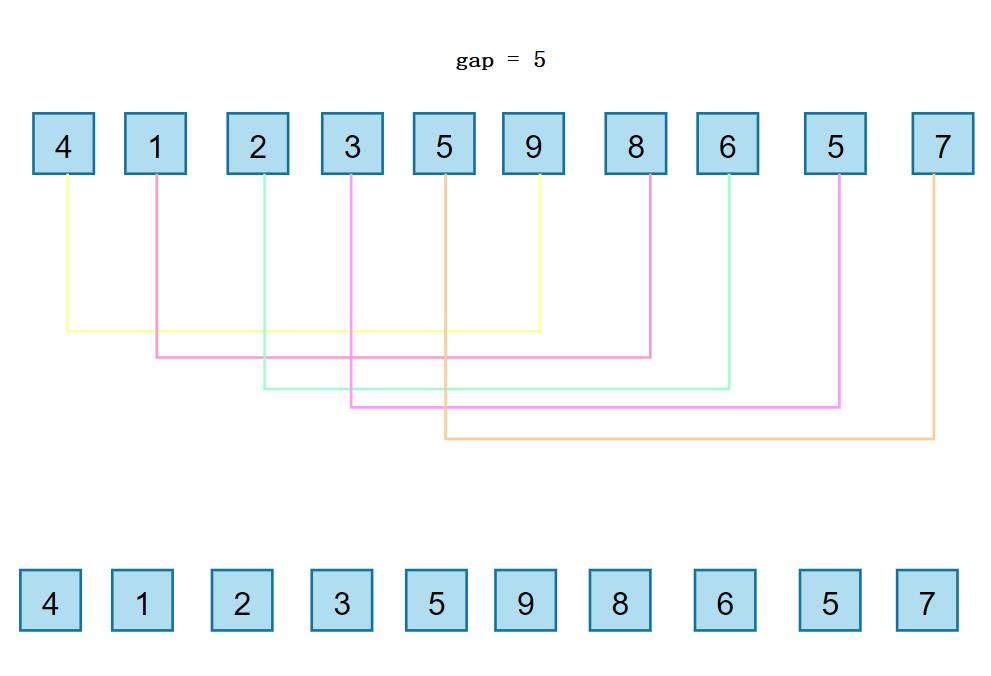
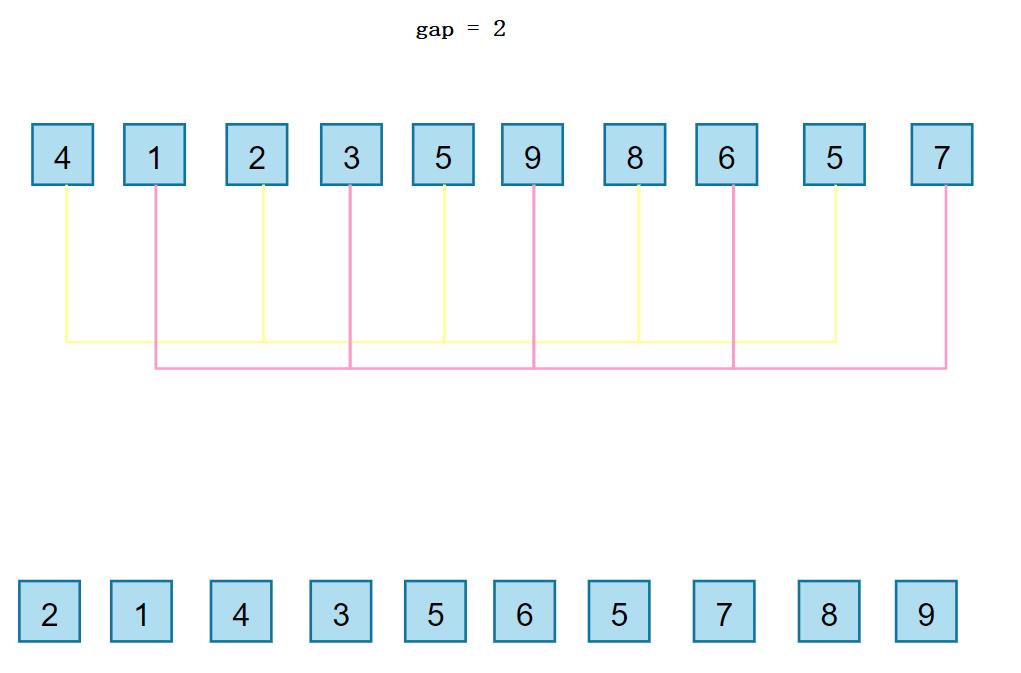
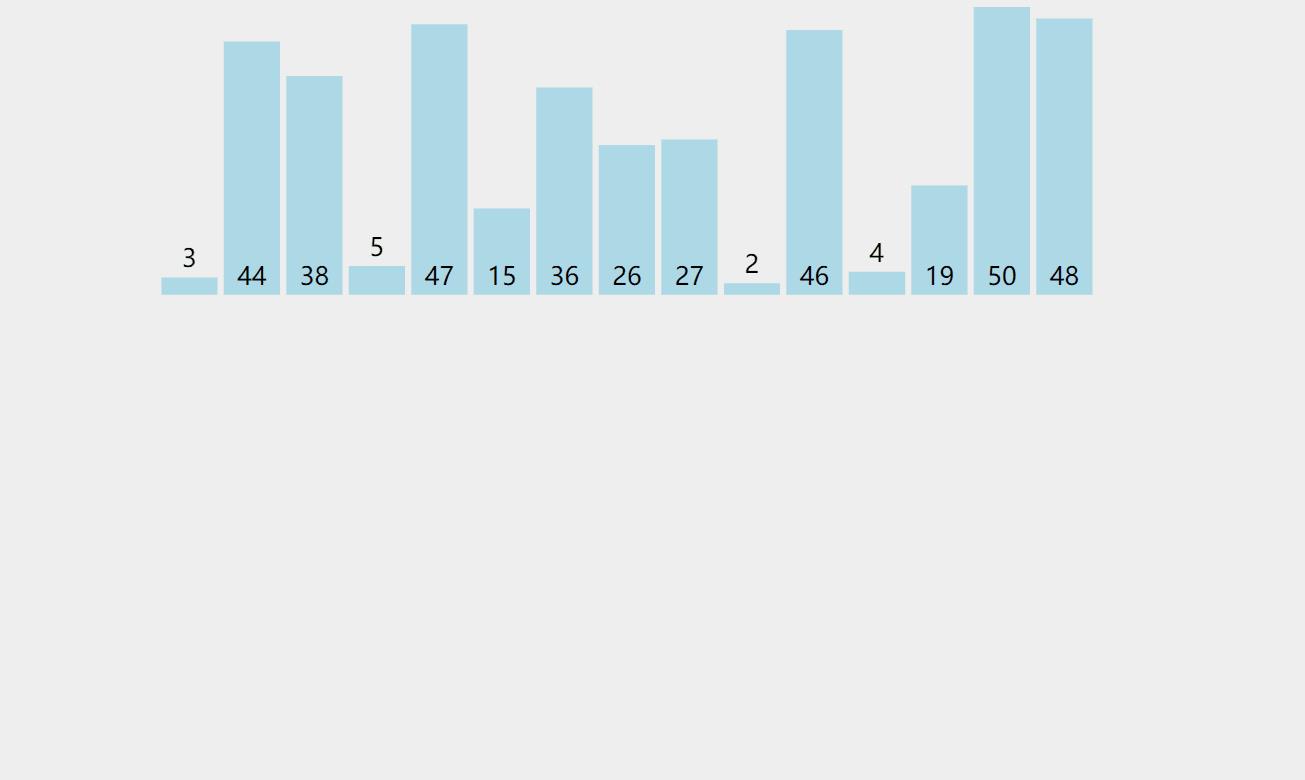
🍋基本思想:希尔排序是建立在直接插入排序之上的一种排序,希尔排序的思想上是把较大的数尽快的移动到后面,把较小的数尽快的移动到后面。先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。(直接插入排序的步长为1),这里的步长不为1,而是大于1,我们把步长这个量称为gap,当gap>1时,都是在进行预排序,当gap==1时,进行的是直接插入排序。
🍋可以先给大家看一个图解:
看一下下面动图演示的过程:

我们可以先写一个单趟的排序:
int end = 0;
int x = a[end + gap];
while (end >= 0)
if (a[end] > x)
a[end + gap] = a[end];
end -= gap;
else
break;
a[end + gap] = x;
这里的单趟排序的实现和直接插入排序差不多,只不过是原来是gap = 1,现在是gap了。
由于我们要对每一组都进行排序,所以我们可以一组一组地排,像这样:
// gap组
for (int j = 0; j < gap; j++)
int i = 0;
for (i = 0; i < n-gap; i+=gap)
int end = i;
int x = a[end + gap];
while (end >= 0)
if (a[end] > x)
a[end + gap] = a[end];
end -= gap;
else
break;
a[end + gap] = x;
也可以对代码进行一些优化,直接一起排序,不要一组一组地,代码如下:
int i = 0;
for (i = 0; i < n - gap; i++)// 一起预排序
int end = i;
int x = a[end + gap];
while (end >= 0)
if (a[end] > x)
a[end + gap] = a[end];
end -= gap;
else
break;
a[end + gap] = x;
🍋当gap>1时,都是在进行预排序,当gap==1时,进行的是直接插入排序。
🍋gap越大预排越快,预排后越不接近有序
🍋gap越小预排越慢,预排后越接近有序
🍋gap==1时,进行的是直接插入排序。
🍋所以接下来我们要控制gap,我们可以让最初gap为n,然后一直除以2直到gap变成1,也可以这样:gap = gap/3+1。只要最后一次gap为1就可以了。
所以最后的代码实现如下:
void ShellSort(int* a, int n)
int gap = n;
while (gap > 1)// 不要写等于,会导致死循环
// gap > 1 预排序
// gap == 1 插入排序
gap /= 2;
int i = 0;
for (i = 0; i < n - gap; i++)// 一起预排序
int end = i;
int x = a[end + gap];
while (end >= 0)
if (a[end] > x)
a[end + gap] = a[end];
end -= gap;
else
break;
a[end + gap] = x;
🍋时间复杂度和空间复杂度的分析
时间复杂度: 外层循环的次数前几篇博客我们算过很多次类似的,也就是O(logN),
里面是这样算的
:给大家看一下直接插入排序排100w个数据要跑多久
看这时间,比起直接插入排序真的是快了太多。
空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
🍋希尔排序稳定性的分析
我们可以这样想,相同的数被分到了不同的组,就不能保证原有的顺序了,所以说这个排序是不稳定的。
🌏选择排序
🌲直接选择排序
🍆基本思想每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
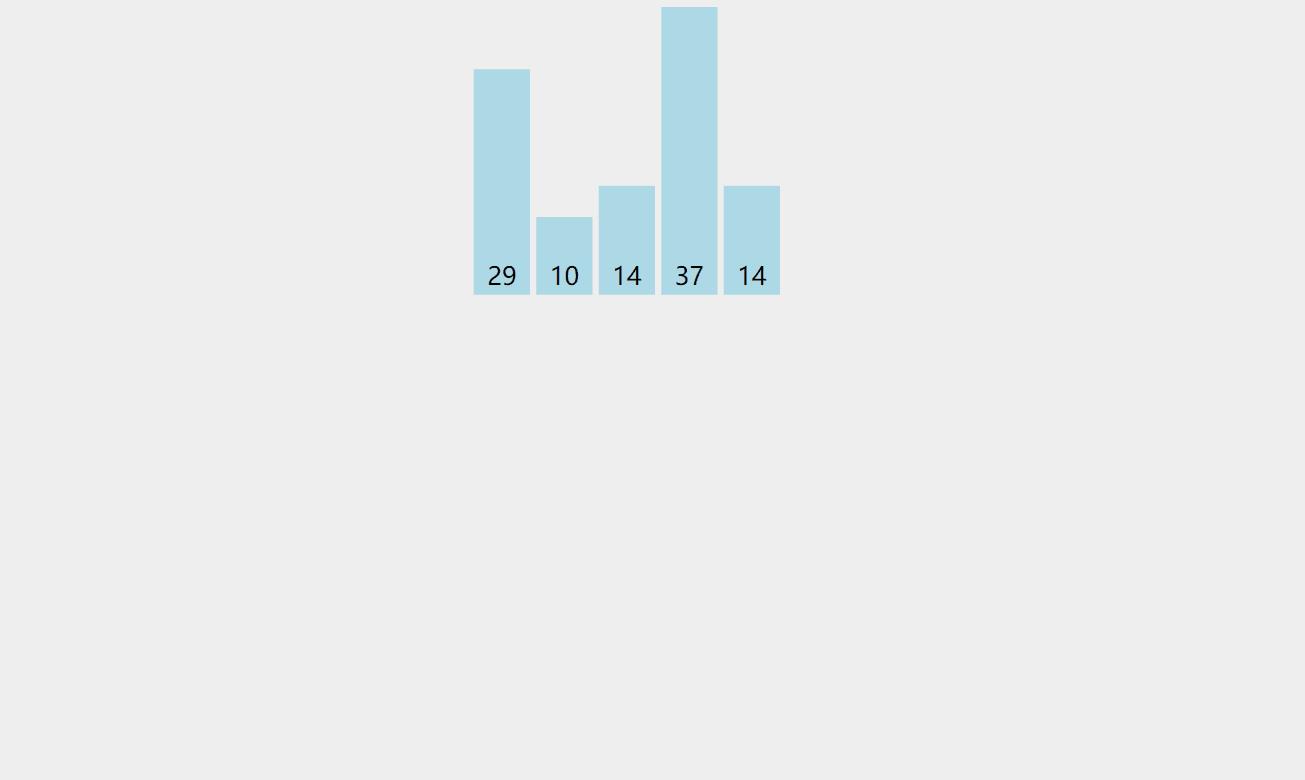
🍆我们先看一下直接选择排序的动图演示:
像上面一样,我们先来实现单趟排序:
int begin = 0;
int mini = begin;
int maxi = begin;
int i = 0;
for (i = begin; i <= end; i++)
if (a[i] > a[maxi])
maxi = i;
if (a[i] < a[mini])
mini = i;
// 如果maxi和begin相等的话,要对maxi进行修正
if (maxi == begin)
maxi = mini;
Swap(&a[begin], &a[mini]);
Swap(&a[end], &a[maxi]);
这里我要说明一下,其中加了一段修正maxi的代码,就是为了防止begin和maxi相等时,mini与begin交换会导致maxi的位置发生变化,最后排序逻辑就会乱了,所以加上一段修正maxi的值得代码。
if (maxi == begin)
maxi = mini;
整体排序就是begin往前走,end往后走,相遇就停下,所以整体代码实现如下:
void SelectSort(int* a, int n)
int begin = 0;
int end = n - 1;
while (begin < end)
int mini = begin;
int maxi = begin;
int i = 0;
for (i = begin; i <= end; i++)
if (a[i] > a[maxi])
maxi = i;
if (a[i] < a[mini])
mini = i;
// 如果maxi和begin相等的话,要对maxi进行修正
if (maxi == begin)
maxi = mini;
Swap(&a[begin], &a[mini]);
Swap(&a[end], &a[maxi]);
begin++;
end--;
🍆时间复杂度和空间复杂度的分析
时间复杂度: 第一趟遍历n-1个数,选出两个数,第二趟遍历n-3个数,选出两个数……最后一次遍历1个数(n为偶数)或2个数(n为奇数),所以总次数是n-1+n-3+……+2,所以说时间复杂度是O(n^2)
最好的情况: O(n^2)(顺序)
最坏的情况: O(n^2)(逆序)
直接选择排序任何情况下的时间复杂度都是 O(n^2),因为不管有序还是无序都要去选数。
🍆给大家看一下直接选择排序排100w个数据要跑多久
空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
🍆直接选择排序稳定性的分析
我们可以这样想
所以说直接选择排序是不稳定的。
🌲堆排序
🌽堆排序我在上上一篇博客已经详细介绍了,大家可以点击这里去看堆排序
🌏交换排序
🍅基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
🐚冒泡排序
🍅基本思想:它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
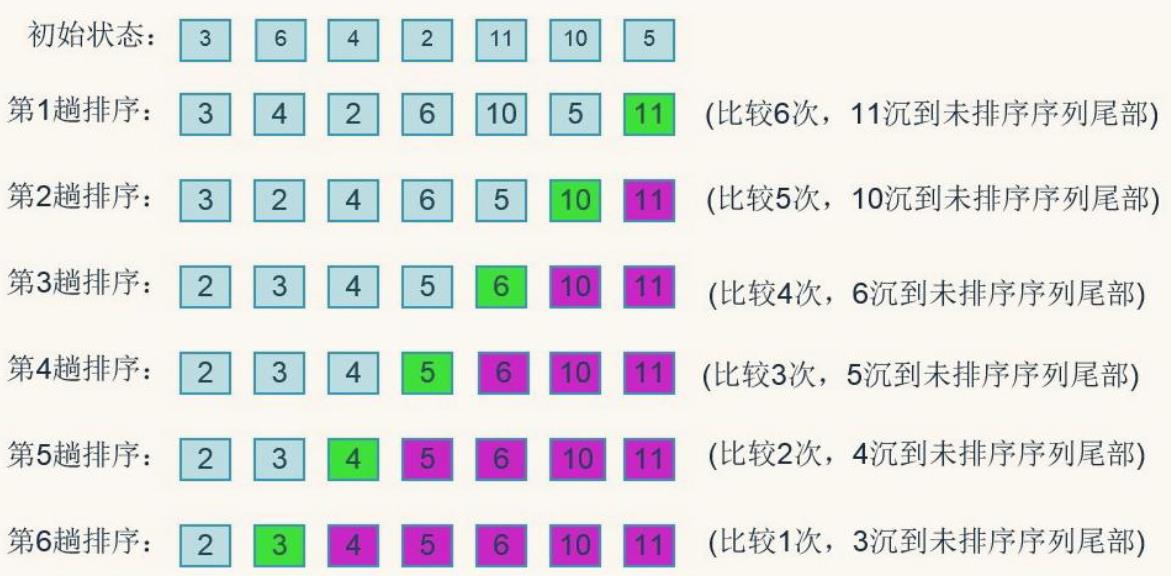
🍅图解如下:
🍅再看一个冒泡排序的动图:
先实现单趟冒泡排序:
int j = 0;
for (j = 0; j < n - 1; j++)
// 比后面的数大就交换
if (a[j] > a[j + 1])
exchange = 1;
Swap(&a[j], &a[j + 1]);
再实现整体的排序:
void BubbleSort(int* a, int n)
int i = 0;
for (i = 0; i < n - 1; i++)
int exchange = 0;
int j = 0;
for (j = 0; j < n - i - 1; j++)
if (a[j] > a[j + 1])
exchange = 1;
Swap(&a[j], &a[j + 1]);
🍅我们再考虑这样一个问题,假如当前的序列已经有序了,我们有什么办法让这个排序尽快结束吗?
这当然是有的,我们可以定义一个exchange的变量,如果这趟排序发生交换就把这个变量置为1,否则就不变,不发生交换的意思就是该序列已经有序了,利用这样一个变量我们就可以直接结束循环了。
优化后的代码如下:
void BubbleSort(int* a, int n)
int i = 0;
for (i = 0; i < n - 1; i++)
int exchange = 0;
int j = 0;
for (j = 0; j < n - i - 1; j++)
if (a[j] > a[j + 1])
exchange = 1;
Swap(&a[j], &a[j + 1]);
// 不发生交换
if (exchange == 0)
break;
🍅时间复杂度和空间复杂度的分析
时间复杂度: 第一趟最多比较n-1次,第二趟最多比较n-2次……最后一次最多比较1次,所以总次数是n-1+n-2+……+1,所以说时间复杂度是O(n^2)
最好的情况: O(n)(顺序)
最坏的情况: O(n^2)(逆序)
所以说冒泡排序在最好的情况下比直接选择排序更优。
🍅给大家看一下冒泡排序排10w个数据要跑多久,因为太慢了,所以这里只排10w
可以看出的是,10w个数冒泡排序都排的很久。
空间复杂度:由于没有额外开辟空间,所以空间复杂度为O(1)
🍅直接选择排序稳定性的分析
冒泡排序在比较遇到相同的数时,可以不进行交换,这样就保证了稳定性,所以说冒泡排序数稳定的。
🐚快速排序(递归版本)
🌰快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
🍍hoare版本
🌰基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
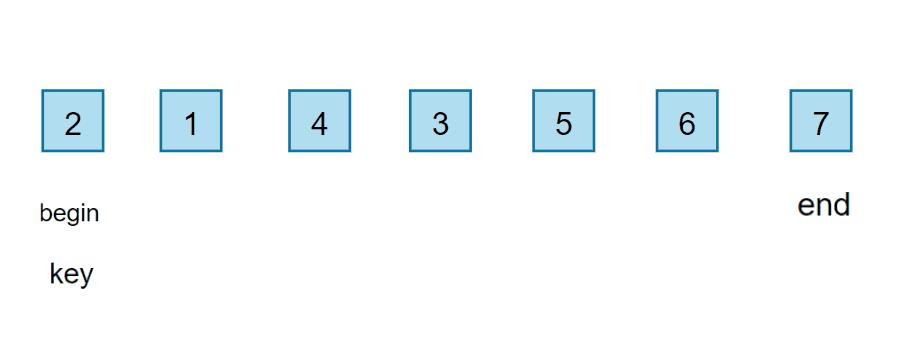
🌰我们先看一个分割一次的动图:
🌰我们要遵循一个原则:关键词取左,右边先找小再左边找大;关键词取右,左边找先大再右边找小。
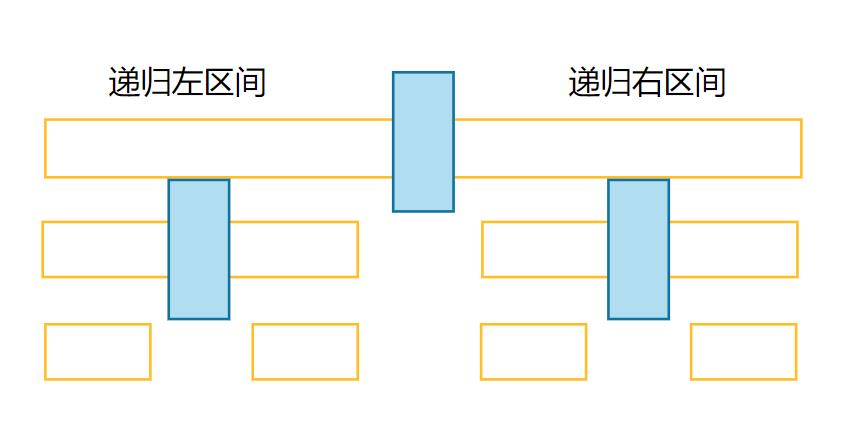
🌰一次过后,2也就来到了排序后的位置,接下来我们就是利用递归来把key左边区间和右边的区间递归排好就可以了,如下:
递归左区间:[left, key-1] key 递归右区间:[key+1, right]
hoare版本找key值代码实现如下:
int PartSort1(int* a, int left, int right)
int keyi = left;
while (left < right)
// 右边找小
while (left < right && a[right] >= a[keyi])
right--;
// 左边找大
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
Swap(&a[keyi], &a[left]);
return left;
快排代码实现如下:
void QuickSort(int* a, int left, int right)
if (left > right)
return;
int div = PartSort1(a, left, right);
// 两个区间 [left, div-1] div [div+1, right]
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
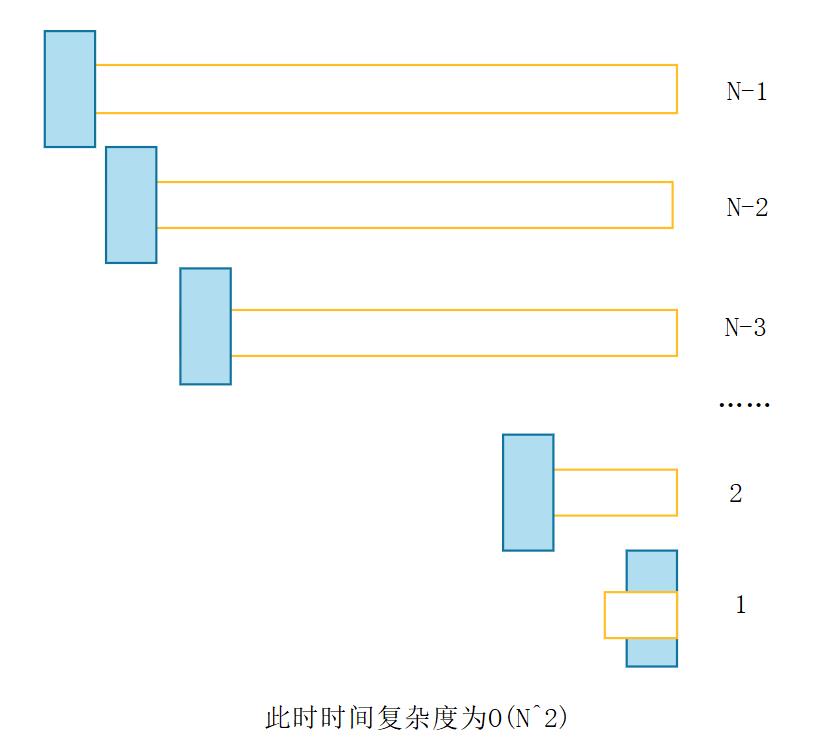
🌰我们考虑这样一种情况,当第一个数是最小的时候,顺序的时候会很糟糕,因为每次递归right都要走到头,看下图:
此时会建立很多函数栈帧,递归的深度会很深,会导致栈溢出(stackover),看下图:
为了优化这里写了一个三数取中的代码,三数取中就是在序列的首、中和尾三个位置选择第二大的数,然后放在第一个位置,这样就防止了首位不是最小的,这样也就避免了有序情况下,情况也不会太糟糕。
下面是三数取中代码:
int GetMidIndex(int* a, int left, int right)
int mid = left + (right - left) / 2;
if (a[mid] > a[left])
if (a[right] > a[mid])
return mid;
// a[right] <= a[mid]
else if (a[left] > a[right])
return left;
else
return right;
// a[mid] <= a[left]
else
if (a[mid] > a[right])
return mid;
// a[mid] <= a[right]
else if (a[left] > a[right])
return right;
else
return left;
所以加上三数取中优化后的代码如下:
int PartSort1(int* a, int left, int right)
int index = GetMidIndex(a, left, right);
Swap(&a[index], &a[left]);
int keyi = left;
while (left < right)
// 右边找小
while (left < right && a[right] >= a[keyi])